матан сука
.pdf
1.
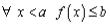
2.
Обозначим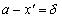 
. Возьмем любое x, для которого 
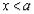, но 
. Как видно из рисунка, из этого следует, что 
. Но тогда, в силу монотонности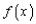 
а)
б)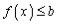 
Поэтому имеем
Выбрасывая лишнее получим, что
или, что то же самое,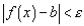 
. По определению предела функции это означает,
что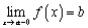 
.
Аналогичные теоремы можно сформулировать и доказать также для монотонно убывающих функций, а так же для пределов слева.
8 Критерий Больцано-Коши
Критерий Коши:
Предел функции f(x) в точке a существует тогда и только тогда, если для каждого ε > 0 найдется такое δ = δ (ε) >0, что
|f(x' ) - f(x" )| < ε,
как только 0 < |x' - a| < δ и 0 < |x' - a| < δ, где x' и x" - любые точки из области определения функции f(x).
если непрерывная функцприниямает два значение, то она принимает и лю
между ними.
|
|
Пусть |
|
дананепрерывная |
|
функциянаотрез |
ке |
Пусть |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
также |
|
и |
|
|
без |
ограничения |
|
общности |
|
предпо |
||||
что |
|
|
|
|
Тогда для |
|
существует |
|
такое, |
|||||
что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
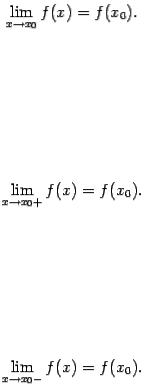
9 эквивалентность бесконечно малых функций
Определение. Если 
то функции a и b
называются эквивалентными бесконечно малыми.
Записывают a ~ b.
10 определения неприрывности функции в точке
Определение 3.1 Пусть функция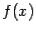 
определена на некотором интервале 
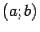, для которого 
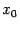-- внутренняя точка. Функция 
называется непрерывной в точке 
,
если существует предел 
при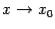 
и этот предел равен значению 
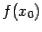, то есть
Пусть функция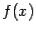 
определена на некотором полуинтервале 
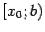, для которого 
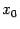- - левый конец. Функция 
называется непрерывной справа в точке 
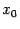, если существует предел 
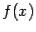при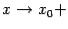 
и этот предел равен значению 
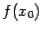, то есть
Пусть, наконец, функция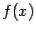 
определена на некотором полуинтервале 
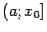, для которого 
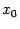-- правый конец. Функция 
называется непрерывной слева в точке 
,
если существует предел 
при 
и этот предел равен значению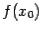 
, то есть
Из теоремы о связи двустороннего предела с односторонними (теорема 2.1) сразу следует, как уже отмечалось в главе 2, что имеет место следующее предложение.
Предложение 3.1 Функция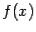 
тогда и только тогда непрерывна в точке 
,
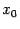когда она непрерывна в точке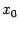 
справа и слева, то есть когда выполнены следующие условия:
1) функция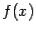 
определена в точке 
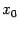и в некоторой окрестности этой точки;
2)существует предел значений функции слева: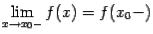 
;
3)существует предел значений функции справа: 
;
4)эти два предела совпадают между собой и со значением функции в точке 
: 
.
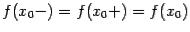11 понятие одностороннего предела функции в точке
Число A' называется пределом слева функции f(x) в точке a:
если
|A' - f(x)| < ε при 0 < a - x < δ (ε).
Аналогично, число A" называется пределом справа функции f(x) в точке a:
если
|A" - f(x) |< ε при 0 < x - a < δ (ε).
Для существования предела функции в точке необходимо и достаточно, чтобы f (a - 0) = f(a + 0).
12Классификация точек разрыва функции
Оп р е д е л е н и е 1. Точкой разрыва первого рода функции y = f (x) называется такая точка x0, в которой функция имеет левый и правый пределы, неравные между собой
Оп р е д е л е н и е 2. Точка x0 (рис. 70) называется точкой разрыва второго рода функции y = f (x), если
хотя бы один из односторонних пределов не существует или равен бесконечности :
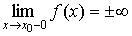и 
.
О п р е д е л е н и е 3. Точка x0 (рис. 71) называется точкой устранимого разрыва y = f (x), если функция в точке неопределена, но односторонние пределы существуют и равны между собой :
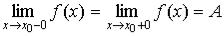, но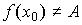 
13 Свойства функций неприрывных на отрезке
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897) - немецкий математик)). Функция,
непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке |
выполняется условие - |
||||
|
. |
|
|
|
|
Доказательство этого свойства основано на том, что функция, непрерывная в точке |
, ограничена в |
||||
некоторой ее окрестности, а если разбивать отрезок |
на бесконечное количество отрезков, которые |
||||
“стягиваются” к точке , то образуется некоторая окрестность точки . |
|
|
|||
Свойство 2: Функция, непрерывная на отрезке |
, принимает на нем наибольшее и наименьшее значения. |
||||
Т.е. существуют такие значения |
и , что |
, причем |
. |
||
Свойство 3: (Вторая теорема Больцано - Коши). Функция, непрерывная на отрезке |
, принимает на этом |
||||
отрезке все значения между двумя произвольными величинами. |
|
|
|||
Свойство 4: Если функция |
непрерывна в точке |
, то существует некоторая окрестность точки |
|||
, в которой функция сохраняет знак. |
|
|
|
||
Свойство 5: (Первая теорема Больцано (1781-1848) - Коши). Если функция |
- непрерывная на |
||||
отрезке |
и имеет на концах отрезка значения противоположных знаков, то существует такая точка |
||||
внутри этого отрезка, где |
. |
|
|
|
|
Свойство 7: Если функция |
определена, монотонна и непрерывна на некотором промежутке, то и |
||||
обратная ей функция |
тоже однозначна, монотонна и непрерывна. |
|
|||
Первая теорема Больцано – Коши
Пусть функция f (x) непрерывна в точке х0 и кроме этого f (x0) ≠ 0. Тогда
существует δ > 0 такое, что для всех х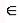
(х0 − δ; х0 + δ) функция f (x) имеет
тот же знак, что и f (х0).
Эта теорема характеризует устойчивость знака непрерывной функции.
Вторая теорема Больцано – Коши
Пусть функция f (x) определена и непрерывна на отрезке [a, b]. Если на концах этого отрезка функция принимает неравные значения f(a) = A, f (b) = B, то, каково бы ни было число m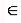
(A, B), найдётся такая точка х =
с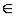 
(a, b), что f (c) = m (рис. 5.17).
Как частный случай имеет место следующее утверждение. Пусть функция f(x) непрерывна на отрезке [a, b] и на концах отрезка имеет значения разных знаков. Тогда существует внутренняя точка отрезка с
(a, b), в которой f(c) = 0.
Данная теорема имеет простой геометрический смысл: непрерывная кривая при переходе из одной полуплоскости, граница которой является ось абсцисс, в другую, пересекает эту ось (рис. 5.18).
Т е о р е м а . Если функция f (x) определена и непрерывна на отрезке [a, b] , то она на этом отрезке принимает по крайней мере один раз любое значение, заключённое между её наименьшими и наибольшими значениями.
Д о к а з а т е л ь с т в о. Будем считать, что А < m < B. Рассмотрим на промежутке [а, b] вспомогательную функцию φ (x) = f (x) − m. Эта функция непрерывна на промежутке [а, b] и на концах его имеет разные знаки: φ
(a) = f (a) − m = A − m < 0 и φ(b) = f(b) − m = B − m > 0. Тогда, по второй теореме Больцано – Коши, между a и b найдётся точка х = с, для которой φ(c) = m. Что и требовалось доказать.
Первая теорема Вейерштрасса
Если функция f (x) определена и непрерывна в замкнутом промежутке [a, b], то она на этом промежутке ограничена.
Д о к а з а т е л ь с т в о . Функция f (х) ограничена на промежутке [а, b], если существуют такие конечные числа m и M, что m ≤ f (х) ≤ М
при a ≤ x ≤ b. Допустим, что функция f (х) при изменении х в промежутке [а, b] оказывается неограниченной. В таком случае для каждого натурального числа n найдётся в промежутке [а, b] такое значение х = хn,
что f ( xn) ≥ n. Однако по лемме Больцано – Вейерштрасса из этой
ограниченной последовательности {xn} можно выделить сходящуюся
частичную подпоследовательность:
Причем, очевидно, х0
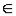[a, b]. Вследствие непрерывности функции в
точке х0 должно быть выполнено
Однако, в силу f (xn) ≥ n имеем
Полученное противоречие и доказывает теорему.
Вторая теорема Вейерштрасса
Непрерывная на отрезке [a, b] функция ограничена и достигает на этом отрезке своей верхней и своей нижней грани (рис. 5.19).
Д о к а з а т е л ь с т в о . Пусть f (x)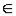 
C[a, b] (функция принадлежит классу
непрерывных функций на отрезке [ |
a |
, |
b |
]) и пусть |
|
. |
Согласно определению верхней грани функции, для каждого n существует такая точка хn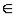
[а, b], что
,
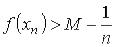Из последовательности xn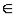
[а, b] можно выделить сходящуюся к
некоторому значению х0 подпоследовательность:
.
В силу непрерывности функции имеем далее
.
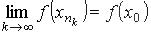В то же время
.
И в пределе f (x0) 
M. Но f (x0) не может быть больше верхней границы
М и, следовательно, f (x0) = М. Что и требовалось доказать.
14 производная функции в точке. Определение. Геометрический смысл
Определение производной функции в точке.
Пусть функция f(x) определена на промежутке (a; b),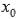 
и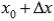 
- точки этого промежутка.Производной функции f(x) в точке 
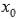называется предел отношения приращения функции к приращению аргумента при 
.
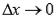Обозначается
Производная функции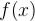 
в точке 
равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
15 Арифметические свойства производных
Если u ( x ) ≡ const , то
u’ ( x ) ≡ 0 , du ≡ 0.
Если u ( x ) и v ( x ) - дифференцируемые функции в точке x0 , то:
( c u )’ = c u’ , d ( c u ) = c du , ( c – const );
( u ± v )’ = u’ ± v’ , ( u v )’ = u’ v + u v’ ,
d ( u ± v ) = du ± dv ; d ( u v ) = v du + u dv ;
16 производная сложной функции
Сложная функция – это функция, аргументом которой также является функция.
Производная сложной функции. Рассмотрим сложную функцию, аргумент которой также является функцией:
h ( x ) = g ( f ( x ) ).
Если функция f имеет производную в точке x0, а функция g имеет производную в точке f ( x0 ), то сложная функция h также имеет производную в точке x0 , вычисляемую по формуле:
h’ ( x0 ) = g’ ( f ( x0 ) ) · f’ ( x0 ) .
17 дифференциал функции. Определение. Геометрический смысл
Определение. Дифференциалом функции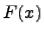 
(обозначается через 
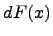) называется следующее выражение:
где dx -- дифференциал x при условии, что функция имеет производную.
Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на dx.
18 теорема о дифференцируемости функции в точке
Т еорема
Дл я т ого, чтобы фу нкция y=f(x) была дифференцируема в т очке x0, необходимо и достаточно, чт обы она в эт ой т очке имела конечную производную.
Доказат ельство
Необходимость. Предположим: фу нкция дифференцируема в т очке x0, т .е. y=A·Δx+α( x)·Δx. Разделив обе части данного равенства на x, получим: x y=A+α( x).
Из определения производной фу нкции в т очке: y/(x0)=lim x→0 x y=lim x→0(A+α( x))=A. Т.е. полу чили, что существует конечная производная фу нкции в т очке x0 и y/(x0)=A.
Дост аточность. Пу сть существует конечная производная y/(x0) R . Покаж ем
дифференциру емость фу нкции. y/(x0)=lim x→0 x |
y. |
Есл и фу нкция f(x) имеет конечный предел b при |
x→0 , т о ее можно представить: f(x)=b+α(x) |
(α(x)→0) . Исходя из эт ого: x y=y/(x0)+α( x), где lim x→0α( x)=0, y=y/(x0)·Δx+α( x)·Δx
→ A=y/(x0) . Теорема доказана.
19 инвариантность формы первого дифференциала
Инвариантность формы первого дифференциала
Если x - независимая переменная, то dx = x - x0 (фиксированное приращение). В этом случае имеем
df(x0) = f'(x0)dx. (3)
Если x = φ(t) - дифференцируемая функция, то dx = φ'(t0)dt. Следовательно,
т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.
20 основные теоремы дифференциального исчисления
1.Теорема. Ролля. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах обращается в нуль g(a)=g(b)=0, то существует по крайней мере одна точка a < c < b в которой производная g обращается в нуль g (c)=0.
Доказательство. Так как функция непрерывна на [a,b], то она имеет на этом отрезке наибольшее (M) и наименьшее значение m. Пусть g(c) - наибольшее значение.
Отсюда
|
|
|
|
|
g(c+x) g(c) |
0, |
x > 0 |
|
|
||
|
x |
|
|
|
|
|
|
|
g(c+ x) g(c) |
0, |
x < 0 |
|
|
||
|
x |
|
|
Переходим к пределу и получаем одновременно g (с) 0 и g (с) 0, следовательно, g (с)=0.
Пример функции, для которой не выполняется условие теоремы, поэтому производная внутри отрезка в 0 не обращается
y=1 (x2)1/3
2.Теорема. Лагранжа. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка, то существует по крайней мере одна точка a < c < b в которой выполняется равенство
g(b) g(a)=g (c)(b a)
Доказательство. Применим теорему Ролля к функции
g(x) g(a) (x a)Q,
где
Q=(g(b) g(a))/(b a)
3.Теорема. Коши. Если функции g(x) и h(x) непрерывны на отрезке [a,b], дифференцируемы во всех внутренних точках этого отрезка,
причем h(x) 0 внутри отрезка [a,b], то существует точка a < c < b в которой выполняется равенство
g(b) g(a) = g (c) h(b) h(a) h (c)
4. Доказательство. Применим теорему Ролля к функции
g(x)g(a) (h(x)h(a))Q,
5. где
Q=(g(b)g(a))/(h(b)h(a))
6.Теорема. Лопиталя. Пусть функции g(x) и h(x) на некотором отрезке [a,b] удовлетворяют условиям теоремы Kоши и обращаются в 0 в точке x=a, т.е. g(a)=h(a)=0, тогда если существует предел отношения g (x)/h (x)
при x a, то существует и
lim g(x)/h(x)
x a
7. причем
|
|
lim g(x)/h(x)= |
lim g(x)/h(x). |
x a |
x a |
21 Многочлен Тейлора
Многочлен Тейлора порядка n
22 формула тейлора
Формула Тейлора
(Rn(x) - остаточный член формулы Тейлора).