матан сука

Остаточный член формулы Тейлора

Вформе Лагранжа:

Вформе Коши:

Вформе Пеано:

при

В интегральной форме:

23 разложение элементарных функций с помощью формулы маклорена

Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:

где Rn − остаточный член в форме Лагранжа определяется выражением

Если приведенное разложение сходится в некотором интервале x, т.е. 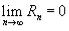, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.

Если a = 0, то такое разложение называется рядом Маклорена:

Разложение некоторых функций в ряд Маклорена

24 критерий постоянства функции на интервале

Критерий постоянства: Функция 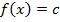на тогда и только тогда, когд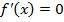а на .

Доказательство:

а)Необходимость: Пусть на .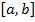

Тогда

б)Достаточность: Пусть и 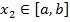. Тогда

1 критерий монотонности функции

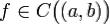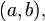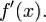(Критерий монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на и имеет в каждой точке производную Тогда

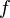не убывает на тогда и только тогда, когда 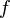не возрастает на 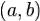тогда и только тогда, когда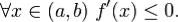

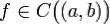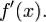(Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на и имеет в каждой точке производную Тогда

если 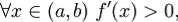то строго возрастает на если то строго убывает на

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале Точнее имеет место

(Критерий строгой монотонности функции, имеющей производную на

1.

2.

Аналогично, 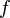строго убывает на интервале тогда и только тогда, когда выполнены следующие два условия:

1.

2.

2 экстремум функции. Необходимое и достаточное условие

Определение экстремума

Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство (f(x1) < f (x2) (f(x1) > f(x2)).

Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f '(x) 0

(f ' (x) 0).

Точка xо называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки xо, для всех точек которой верно неравенство f(x) ≤f(xо) (f(x)

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Точки экстремума

Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f '(xо) = 0, либо f (xо) не существует. Такие точки называюткритическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть xо - критическая точка. Если f ' (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную

f ' (x) в окрестности точки xо и вторую производную 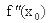в самой точке xо. Если f ' (xо) = 0, >0 (<0), то точка xо является точкой локального минимума (максимума)

функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

3 критерий выпуклости графика функции на интервале

Теорема.

Если функция y=f(x) имеет конечную вторую производную на интервале Х и

если выполняется неравенство 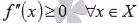( ), то график функции имеет выпуклость направленную вниз (вверх) на Х.

Эта теорема позволяет находитьть промежутки вогнутости и выпуклости функции, нужно лишь на области определения исходной функции решить

неравенства и 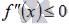соответственно.

Следует отметить, что точки, в которых функция y=f(x) определена, а вторая

производная не существует, будем включать в интервалы вогнутости и выпуклости.

4 теорема о наименьшем и наибольшем значении неприрывной функции на интервале

Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.

Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x1 [a, b] такая, что значение функции f(x)в этой точке будет самым большим из всех ее значений на этом отрезке: f(x1) ≥ f(x). Аналогично найдётся такая точка x2, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x1) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x2 и x2'.

Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример. ледствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.

1 Определение первообразной функции. Теорема о представлении первообразной функции

еорема: любая первообразная для некоторой функции f на промежутке А может быть записана в виде:

F(x) +C, где F(x) – одна из первообразных для данной функции f на промежутке A, а С – некоторая произвольная постоянная.

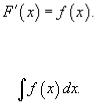
Теорема, приведенная выше, называется еще основным свойством первообразной. Разберем её более подробно, так как в ней скрывается целых два свойства первообразной функции.

1.При подстановке любого числа вместо С в эту формулу получим первообразную функции f на промежутке А.

2.Если взять любую первообразную Ф для функции f на некотором промежутке А. То для этой производной можно подобрать некоторое число С, такое что для любого х будет выполняться следующее равенство: Ф(х) = F(x)+C.

2 неопределённий интеграл. Определение. Свойства.

еопредел нный интеграл для функции 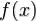— это совокупность всех первообразных данной функции.

Функция F(x) называется первообразной функции f(x), если

Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функцииf(x) и обозначается как

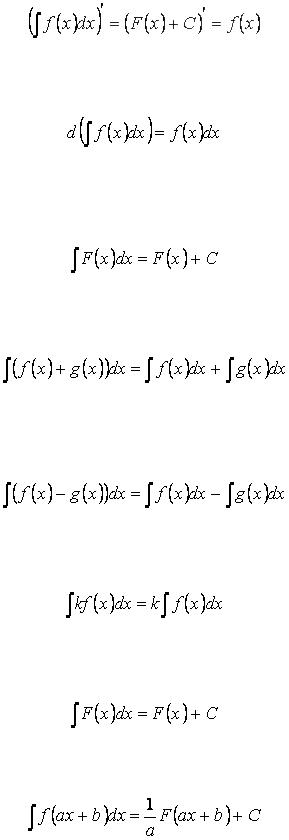
Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если , то

Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению

Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сум ме этой функции и произвольной константы

Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов

Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов

Свойство 6. Постоянный множитель можно выносить за знак интеграла

Свойство 7. Если

то