
discr_math
.pdf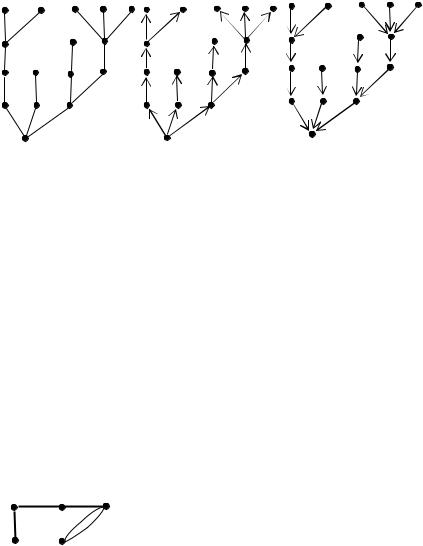
55
T1 |
T2 |
T3 |
|
v0 |
v0 |
v0 |
|
Рис 4. 38 |
|||
|
|
||
На рис. 4. 38 приведены примеры дерева с корнем T1 , его ориенти- |
|||
рованного дерева T2 |
и сети сборки T3 . |
||
Деревья графов |
|
|
|
Пусть дерево |
T является подграфом графа G . Ребра графа |
||
G , которые принадлежат дереву T , называются ветвями дерева T , |
|||
а ребра, не принадлежащие дереву T , хордами относительно де- |
|||
рева T . Если T есть суграф G , |
то есть вершины дерева T совпа- |
||
дают с вершинами графа G , то говорят, что дерево T покрывает |
|||
граф G . В этом случае дерево T |
называют остовом или каркасом |
||
графа G .
Существует простой способ определить количество различных
остовов мультиграфа G с n вершинами. Для этого нужно записать
1 |
2 |
|
|
3 |
матрицу A размера n n, по главной диаго- |
|
|
нали которой выписаны степени вершин, а |
|||
|
|
|
|
||
|
|
|
|
|
|
5 |
|
|
4 |
|
элементы aij aji равны взятому со знаком |
|
|
|
|||
Рис. 4.39 |
|
|
|
||
минус числу ребер, связывающих вершины

56
i и j , i j 23. Вычислив минор любого элемента главной диагонали
матрицы A, получим искомое число возможных остовов графа24.
Например, для графа на рис. 4.39 имеем:
|
2 |
1 |
0 |
0 |
1 |
|
|
|
|
2 |
0 |
0 |
1 |
|
||
|
|
|
4 1 |
1 |
|
|
|
|
|
|
|
|||||
|
1 |
1 |
|
|
|
|
0 |
3 |
2 |
0 |
|
|||||
A |
|
0 |
1 |
3 |
2 |
0 |
|
; |
М |
|
|
50. |
||||
|
0 |
2 |
4 |
1 |
||||||||||||
|
|
|
1 |
2 |
4 |
|
|
|
|
22 |
|
|
||||
|
0 |
1 |
|
|
|
|
1 |
0 |
1 |
3 |
|
|||||
|
|
1 |
1 |
0 |
1 |
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, существует 50 различных деревьев, покры-
вающих этот граф. Один из 50 остовов мультиграфа G изображен на рис. 4.39 жирными линиями.
Экстремальные графы
Класс практических задач, достаточно успешно решаемых методами теории графов, требует связать n пунктов наиболее экономичным образом. Например, необходимо построить автомобильные дороги, связывающие n дачных поселков, так, чтобы их суммарная длина была наименьшей. Любые два поселка должны быть связаны дорогой либо непосредственно, либо дорогами, проходящими через другие поселки. Похожие задачи возникают при прокладке водопроводов, газопроводов, линий связи и т. п.
На языке теории графов задачи такого рода формулируются следующим образом. Каждому ребру ui полного графа с n вершинами при-
писывается вес i , выражающий численно расстояние, стоимость или
иную величину, характеризующую взаимосвязь между каждой парой вершин графа. Требуется выявить такой остов этого графа, чтобы суммарный
23Такая матрица называется матрицей Кирхгофа мультиграфа G .
24Следствие теоремы Кирхгофа.
57
n
вес ветвей остова i был минимальным (или максимальным). Та-
i 1
кой остов графа называют его экстремальным деревом.
Поскольку полный граф Kn покрывает nn 2 различных основных деревьев, то решение этой задачи полным перебором вариантов потребовало бы чрезвычайно больших вычислений даже при относительно малых n. Уже при n 9 таких вариантов больше миллиона.
Для решения задач такого рода разработаны достаточно эффективные алгоритмы. Далее мы воспользуемся одним из них алгоритмом Дж. Краскала. Его суть состоит в следующем. На первом шаге выбирается первая ветвь искомого остова это ребро графа с наименьшим (наибольшим) весом. Затем на каждом следующем шаге рассматривается минимальное (максимальное) по весу ребро и, если оно не образует цикла с ранее выбранными ветвями, вводится в остов. Построение заканчивается после отбора для остова n 1 ребер.
Теорема 4.13. Алгоритм Краскала позволяет построить экстремальный граф любого связного графа.
Пример 4.3. Необходимо построить автомобильные дороги, связывающие девять поселков так, чтобы их суммарная длина была наименьшей. Любые два поселка должны быть связаны дорогой либо непосредственно, либо дорогами, проходящими через другие поселки. Известно расстояние между поселками (в км):
|
П2 |
П3 |
П4 |
П5 |
П6 |
П7 |
П8 |
П9 |
П1 |
25 |
13 |
32 |
34 |
35 |
49 |
19 |
14 |
П2 |
|
12 |
31 |
59 |
60 |
73 |
34 |
40 |
П3 |
|
|
19 |
47 |
48 |
61 |
32 |
27 |
П4 |
|
|
|
65 |
66 |
80 |
51 |
46 |
П5 |
|
|
|
|
26 |
15 |
28 |
48 |
П6 |
|
|
|
|
|
19 |
54 |
35 |
П7 |
|
|
|
|
|
|
42 |
61 |
П8 |
|
|
|
|
|
|
|
33 |
На первом шаге выбираем самый короткий участок искомой сети дорог, связывающей поселки. Это дорога длиною 12 км между поселками П1 и П2. Затем добавляем к ней дороги между П1 и П3 (13 км), П1 и П9 (14 км), П5 и П7 (15 км), П3 и П4 (18 км). Следующее минимальное расстояние между поселками равно 19 км. Таково расстояние между П1 и П8 и между

58
П6 и П7. Так как обе эти дороги не образуют цикла с уже отобранными дорогами, то обе они добавляются в список. Следующие по длине (25 км и 26 км) дороги между П1, П2 и П5, П6 нельзя добавлять в наш список иначе появятся циклы: П1, П2, П3, П2 или П5, П6, П7, П5. Восьмая и последняя дорога искомого минимального остова имеет длину 28 км, она проходит между П5 и П8. Минимальный остов, связывающий девять поселков, изображен на рис. 4.40. Минимальная длина дорог, связывающих поселки, равна 138 км.
П4 |
П9 |
П6 |
П1
П3 
П7
П2

 П5 П8
П5 П8
Рис.4.40
Экстремальное дерево может быть построено для произвольного графа, а не только для полного графа. Например, связи между некоторыми вершинами могут быть нежелательными или недопустимыми.

1
Раздел 5
Расчетно-графические задания
Задание 1. Операции над множествами
Универсальное множество состоит из 26 строчных букв латинского алфавита. Заданы множества A, B, C и D (табл.5.1). Вычислить мощность множеств X и Y.
Пример выполнения задания
Условие. Даны множества A={a,e,f,j,k}, B={ f,i,j,l,y}, C={ j,k,l,y}, D={i,j,s,t,u,y,z}. Вычислить мощность множеств
X (A C) (B C) и Y (A B) (D\C).
Решение.
1. Определим элементы множества X (A C) (B C).
Для этого найдем сначала пересечение множеств A C . Элементы j и k одновременно принадлежат множеству A и C. Следовательно, A C {j,k}. Аналогично, B C {j,l, y}. Таким образом, объ-
единение A C и B C состоит из четырех элементов {j,k,l, y}.
Мощность множества X (A C) (B C) равна 4.
2. Определим элементы множества Y (A B) (D\C).
Найдем дополнение B . Универсальное множество по условию за-
дания состоит их 26 букв {a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x, y,z}. Если отсюда исключить 5 элементов множества B, то получим
множество B из 21 элемента {a,b,c,d,e,g,h,k,m,n,o,p,q,r,s,t,u,v,w,x,z}.
Пересечение множеств A B состоит из элементов {a,e,k}, т.е. всех элементов множества A , которые не принадлежат B1.
1 A\ B

2
Для нахождения разности множеств D \C вычеркнем из множества D={i,j,s,t,u,y,z} элементы {j,y}, принадлежащие
C={ j,k,l,y}. Получим D \C ={i,s,t,u,z}. В итоге
Y (A B) (D\C)={a,e,k,i,s,t,u,z} .
Мощность множества Y |
равна 8. В данном случае множест- |
||||
ва D \C и A |
|
не пересекаются и мощность объединения равна |
|||
B |
|||||
сумме мощностей слагаемых |
|
||||
Card Y Card(A |
|
) Card(D\C)=3+5. |
|||
B |
|||||
Табл.5.1 |
Задание 1 |
||||
1A={ a,e,f,k,t}, B={ f,i,j,p,y}, C={ j,k,l,y}, D={i,j,s,t,u,y,z}
X (A B) (D C), Y (A B) (C \ D).
2A={ b,h,m,o,r}, B={j,k,o,u,y}, C={g,h,j}, D={g,j,q}
X (A C) (D B), Y (A B) (C \ D).
3A={ c,m,n,o,q}, B={c,d,m,w}, C={m,n,q}, D={c,m,p},
X (A B) C, Y (A B) (C \ D).
4A={ b,d,l,p}, B={b,d,e,l,p,x}, C={k,l,p,t}, D={d,k,o,p,q,u,v},
X (A\ B) (C D),Y (A B) (C \ D).
5A={ c,e,h,n}, B={e,f,k,n,x}, C={b,c,h,p,r,s}, D={b,e,g},
X (A\ B) (C D),Y (A B) (C \ D).
6A={a,b,f,g,i}, B={c,f,g,i,s,v}, C={a,g,h,i}, D={f,w,x},
X (A B) C, Y (A B) (C \ D).
7A={b,f,g,m,o}, B={b,g,h,l,u}, C={e,f,m}, D={e,g,l,p,q,u,v},
X (A C) B, Y (A B) (C \ D).
8A={b,c,h,i,j}, B={e,h,i,s,w}, C={a,b,j,k,l,m}, D={a,h,i,w,x},
X (A\C) B, Y (A B) (C \ D).
9A={a,e,f,i}, B={a,b,k,n}, C={e,f,n,o,w,x}, D={a,d,e,o,p,t,u},
X (A B) D, Y (A B)\(C D) .
10A={a,b,h,j,l}, B={b,c,h,l,r,v}, C={j,k,n,t,z}, D={b,i,k,v,w},

3
Табл.5.1 |
Задание 1 |
||||
|
|
|
|
|
|
X (A D) C, Y ( |
|
|
|
)\(C D) . |
|
A |
B |
|
|||
11A={a,h,k}, B={c,d,h,p,r}, C={h,i,s}, D={c,g,j,v,w},
X (A B) C, Y (A B)\(C D) .
12A={a,d,k,l,o,s}, B={d,e,k,s,u,x}, C={o,p,w}, D={d,n,r,y,z},
X (A\ B) (C D),Y (A B)\(C D) .
13A={a,b,g,k,m,p}, B={b,e,f,l,r}, C={k,l,w,x}, D={e,j,o,p,q,u,v},
X (A\ B) (C D),Y (A B)\(C D) .
14A={a,f,i,n,o}, B={f,g,o,p,z}, C={i,j,u,w}, D={f,h,n,t,u,y,z},
X (A B) C, Y (A B)\(C D) .
15A={a,b,h,k,o,r}, B={b,g,h,l,s}, C={k,l,z}, D={g,j,p,q,u,v},
X (A C) B, Y (A B)\(C D) .
16A={a,e,g,o,p}, B={e,h,i,o,u}, C={g,h,p,s,t,w}, D={f,h,n,s,t,x,y},
X (A\C) B, Y (A B)\(C D) .
17A={b,k,n,o,q}, B={a,b,k,u}, C={o,p}, D={a,m,n,y,z},
X (A B) D, Y (A D) (C \ B).
18A={a,b,c,d,e,r}, B={b,c,d,f,n,y},C={b,c,h,k,l,s}, D={a,b,r,s,w,x},
X (A D) C, Y (A D) (C \ B).
19A={b,e,g,h,k,s}, B={c,g,p,q}, C={f,g,s,x,y,z}, D={a,c,d,g,u,v,z},
X (A B) C, Y (A D) (C \ B).
20A={a,b,c,e,t}, B={b,c,d,e,m,u}, C={b,c,f,g,h,u}, D={a,d,q,r,v,w},
X (A\ B) (C D),Y (A D) (C \ B).
21A={b,d,f,g,l,u}, B={d,e,f,m,n,z}, C={h,i,r,x,y}, D={a,e,f,k,r,s,x},
X (A\ B) (C D),Y (A D) (C \ B).
22A={b,d,j,n,t,v}, B={f,g,j,r,t,x}, C={o,p,x}, D={a,f,m,s,x,y},
X (A B) C, Y (A D) (C \ B).
23A={b,c,g,i,w}, B={e,g,h,q,w}, C={c,d,k,l,y}, D={a,g,h,u,v,z},
X (A C) B, Y (A D) (C \ B).
24A={a,b,d,l,x}, B={d,e,h,i,n,u}, C={e,f,m,n}, D={a,c,h,k,r,s,w,x},

4
Табл.5.1 |
|
|
Задание 1 |
||
|
|
|
|
|
|
X (A\C) |
|
, |
Y ( |
|
D) (C \ B). |
B |
A |
||||
25A={c,g,h,k,y}, B={a,b,k,n,u}, C={i,j,o,y,z}, D={a,b,f,g,y,z},
X (A B) D, Y (A\ D) (C \ B).
26A={c,d,k,l,m,z}, B={b,c,d,n,w}, C={m,n,y}, D={b,j,l,r,s,w,x},
X (A D) C, Y (A\ D) (C \ B).
27A={c,g,h,i,j}, B={c,d,i,o,s}, C={i,j,r,z}, D={b,c,f,i,w,x},
X (A B) C, Y (A\ D) (C \ B).
28A={c,f,h,l,o}, B={d,e,f,p,w}, C={j,k}, D={b,d,g,k,t,u,y,z}
X (A\ B) (C D),Y (A\ D) (C \ B).
29A={c,f,g,k}, B={e,f,g,m,q}, C={h,i,r,w,x}, D={b,e,j,u,v,z},
X (A\ B) (C D),Y (A\ D) (C \ B).
30A={b,c,h,o}, B={d,f,g,o,v,y}, C={d,e,j,k}, D={a,b,f,g},
X (A B) C, Y (A\ D) (C \ B).
Задание 2. Транзитивное замыкание отношения
Отношение задано матрицей (табл. 5.2). Исследовать отношение на симметрию, антисимметрию, асимметрию, рефлексивность, антирефлексивность. Найти транзитивное замыкание отношения. Построить граф отношения и его транзитивного замыкания.
Пример выполнения задания
Условие. Матрица M отношения имеет следующий вид:
1 |
0 |
0 |
1 |
|
|
|
|
M 1 |
0 |
0 |
0 . |
0 |
0 |
0 |
0 |
|
0 |
1 |
|
0 |
1 |

5
Табл. 5.2

6
Табл. 5.2
Исследовать свойства отношения и построить его транзитивное замыкание.
Решение
1.Данное отношение не является симметричным, так как матрица несимметрична. Например, пара (2,1) принадлежит , а пара (1,2) ему не принадлежит.
2.Отношение антисимметрично, так как нет ни одной пары
mij mji 1, |
i j. |
3.Отношение антисимметрично, но не асимметрично, так как на диагонали матрицы имеются элементы равные 1. .
4.Все диагональные элементы матрицы рефлексивного отношения равны 1. Данное отношение не является рефлексивным.
5.Отношение не обладает свойством антирефлексивности, так как диагональ матрицы ненулевая.
