1.3. Двойственная задача линейного программирования

_{С каждой задачей линейного программирования можно некоторым образом сопоставить другую задачу ЛП, называемую двойственной по отношению к исходной (прямой).}

_{Под двойственной задачей понимается вспомогательная задача линейного программирования, формулируемая с помощью определённых правил непосредственно из условий прямой задачи. Заинтересованность в определении оптимального решения прямой задачи путём решения двойственной к ней задачи обусловлена тем, что вычисления при решении ДЗ могут оказаться менее сложными. Трудоёмкость вычислений при решении ЗЛП в большей степени зависит от числа ограничений, а не от количества переменных.}

_{Дадим определение двойственной задачи по отношению к прямой задаче линейного программирования, состоящей, в нахождении максимального значения функции}

_{функции}

f =c₁x₁ + c₂x₂ +…+ c_nx_n→max (1.4)

при условиях:

a₁₁x₁ + a₁₂x₂ +…+ a_1nx_n ≤ b₁

a₂₁x₁ + a₂₂x₂ +…+ a_2nx_n ≤ b₂

… (1.5)

a_m1x₁ + a_m2x₂ +…+ a_mnx_n ≤ b_m

x_j ≥ 0 (j = 1, 2,…m, m ≤ n).

Задача, состоящая в нахождении минимального значения функции

f*=b₁y₁ + b₂y₂ +…+ b_my_m→min (1.6)

при условиях:

a₁₁y₁ + a₁₂y₂ +…+ a_m1y_m ≥ c₁

a₁₂y₁ + a₂₂y₂ +…+ a_m2y_m ≤ c₂

… (1.7)

a_1ny₁ + a_2ny₂ +…+ a_mny_m ≤ c_m

y_i ≥ 0 (i = 1, 2, … k ≤ m)

_{называется двойственной по отношению к задаче (1.4) – (1.5). Задачи (1.4) – (1.5) и (1.6) – (1.7) образуют пару задач, называемую в линейном программировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача составляется согласно следующим правилам:}

_{Целевая функция исходной задачи задается на максимум, а целевая функция двойственной– на минимум.}

1. _{Матрица}

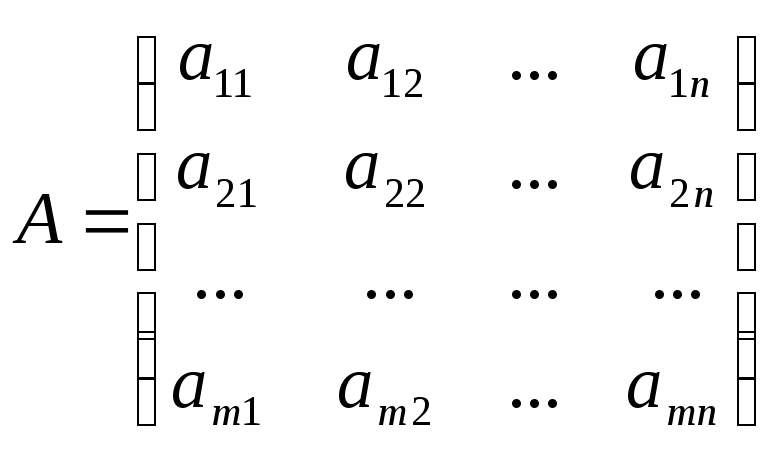_(1.8)

2. _{составленная из коэффициентов при неизвестных в системе ограничений (1.5) исходной задачи, и аналогичная матрица}

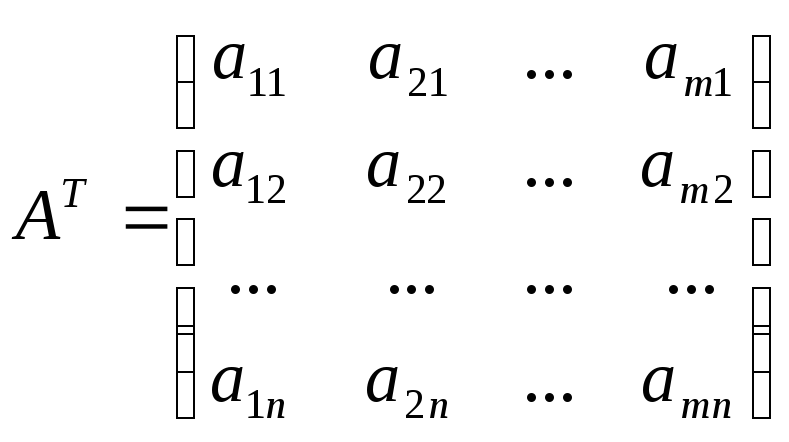_(1.9)

_{в двойственной задаче получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов – строками).}

3. _{Число переменных в двойственной задаче равно числу ограничений в системе (1.5) исходной задачи, а число ограничений в системе (1.7) двойственной задачи – числу переменных в исходной задаче.}

4. _{Коэффициентами при неизвестных в целевой функции (1.6) двойственной задачи являются свободные члены в системе (1.5) исходной задачи, а правыми частями в соотношениях системы (1.7) двойственной задачи – коэффициенты при неизвестных в целевой функции (1.4) исходной задачи.}

5. _{Если i–е соотношение в системе (1.5) исходной задачи является неравенством, то j–я переменная двойственной задачи yj ≥ 0. В противном случае переменная уj может принимать как положительные, так и отрицательные значения.}

_{Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (1.5) прямой задачи и соотношения (1.7) двойственной задачи являются неравенствами вида “ ”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.}

_{Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (1.5) прямой задачи и соотношения (1.7) двойственной задачи являются неравенствами вида “ ”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.}

_{Если одна из задач двойственной пары (1.4) – (1.5) или (1.6) – (1.7) имеет оптимальный план, то и другая имеет оптимальный план, и значения целевых функций задач при их оптимальных планах равны между собой, т. е. f max = f*min.}

_{Если же целевая функция одной задачи из двойственной пары неограниченна (для исходной – сверху, для двойственной – снизу), то другая задача вообще не имеет планов.}