
- •1. Абсолютная и относительная погрешности числа(определения, предельные погрешности, примеры)
- •2.Десятичная запись приближенного числа. Значащая цифра. Верные знаки числа(определение верных и значащих цифр, примеры; теория о связи относительной погрешности и числа верных знаков).
- •3.Погрешность суммы и разности(вывод абсолютной и относительной погрешности из общих формул решения основной задачи теории погрешности).
- •4. Погрешности произведения и частного(вывод относительной и абсолютной погрешности из общих формул решения основной задачи теории погрешности).
- •5. Метод Гаусса(прямой и обратный ход), условия применимости метода.
- •Описание метода
- •Условие совместности
- •7.Метод Ньютона (метод касательных прямых) для уточнения изолированного корня алгебраического или трансцендентного уравнения.
- •Алгоритм
- •Метод простых итераций для численного решения алгебраических или трансцендентных уравнений. (Суть метода и геометрическая интерпретация).
- •Достаточные условия сходимости метода простой итерации (теоремы, оценки погрешностей).
- •Конечные разности различных порядков. Таблицы разностей.
- •Постановка задач аппроксимации функции, общей задачи интерполирования, простейшей задачи интерполирования.
- •Первая интерполяционная формула Ньютона (общая формула и формулы для линейного и квадратичного интерполирования).
- •Интерполяционный многочлен Лагранжа (вывод, доказательство единственности).
- •15. Постановка задачи численного интегрирования.
- •16. Вывод квадратурных формул Ньютона - Котеса.
- •17. Формула трапеции и ее остаточный член(вывод основной и общей формулы, запись остаточного члена, оценка шага интегрирования)
- •18. Формула Симпсона и ее остаточный член (вывод основной и обобщенной формул, запись остаточного члена, оценка шага интегрирования)
- •19. Постановка задачи численного решения обыкновенных дифференциальных уравнений.
- •20.Метод Эйлера для решения скалярной задачи Коши (вывод расчетной формулы, геометрический смысл) и его недостатки.
- •21.Метод Эйлера для систем дифференциальных уравнений.
- •Усовершенствованный метод Эйлера.
- •Модифицированный метод Эйлера Коши.
7.Метод Ньютона (метод касательных прямых) для уточнения изолированного корня алгебраического или трансцендентного уравнения.
f(x)=0 (1)
пусть
![]() является корнем решения (1) этот корень
отделен на отрезке
является корнем решения (1) этот корень
отделен на отрезке![]() причем
причем не прерывна и сохраняет опред. знаки на
отрезке [a,b]
найдем какой-либо способ
не прерывна и сохраняет опред. знаки на
отрезке [a,b]
найдем какой-либо способ
![]() (n-е
приближение) к корню.
(n-е
приближение) к корню.
Тогда точное
решение уравнение (1) можно записать как
существование некоторого приближения
![]() уточним
уточним![]() так как функцияf(x)
не прерывна на отрезке [a,b],
то с учетом равенства (2) можно записать
так как функцияf(x)
не прерывна на отрезке [a,b],
то с учетом равенства (2) можно записать
![]() к данному равенству применим формулу
Тейлора:
к данному равенству применим формулу
Тейлора:
![]()
Тогда с учетом
равенства (3)+(2) следует:
![]()
Геометрически это означает замену небольшой дуги кривой касательной проведенный к некоторой точке кривой по этому метод ньютона называют метод касательных.

![]()
Иллюстрация метода
Ньютона (синим изображена функция
![]() ,
нуль которой необходимо найти, красным —
касательная в точке очередного приближения
,
нуль которой необходимо найти, красным —
касательная в точке очередного приближения![]() ).
Здесь мы можем увидеть, что последующее
приближение
).
Здесь мы можем увидеть, что последующее
приближение![]() лучше
предыдущего
лучше
предыдущего![]() .
.
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть
![]() —
определённая на отрезке
—
определённая на отрезке![]() и
дифференцируемая. Тогда формула
итеративного исчисления приближений
может быть выведена следующим образом:
и
дифференцируемая. Тогда формула
итеративного исчисления приближений
может быть выведена следующим образом:
![]()
где
![]() —
угол наклона касательной в точке
—
угол наклона касательной в точке![]() .
.
Следовательно
искомое выражение для
![]() имеет
вид:
имеет
вид:
![]()
Если За
![]() взять 0, то точка будет лежать вне отрезка
[a,b]
за начальное приближение берется та
точка значение функции в которой
совпадает со значением второй производной
этой функции в любой точки отрезка
[a,b].
взять 0, то точка будет лежать вне отрезка
[a,b]
за начальное приближение берется та
точка значение функции в которой
совпадает со значением второй производной
этой функции в любой точки отрезка
[a,b].
Алгоритм
Задается начальное приближение
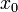 .
.Пока не выполнено условие остановки, в качестве которого можно взять
 или
или (то
есть погрешность в нужных пределах),
вычисляют новое приближение:
(то
есть погрешность в нужных пределах),
вычисляют новое приближение: .
.
Метод простых итераций для численного решения алгебраических или трансцендентных уравнений. (Суть метода и геометрическая интерпретация).
Суть метода:
f(х)=0
(1) непрерывная функция заменим
эквивалентным уравнением
![]() (2).
(2).
Выберем каким либо способом грубое приближение корня и обозначим его х0.
Подставим х0
в правую часть уравнения (2), получим х1=
![]() ,
х2=
,
х2=
![]() …..
хn=
…..
хn=
![]() (3)
(3)
Если последовательность
окажется сходящейся то
![]()
Переходя к пределу
в равенстве (3), получим
![]() Стало быть
Стало быть![]() является
корнем уравнения (2)
является
корнем уравнения (2)![]() и
уравнения (1).
и
уравнения (1).
![]()
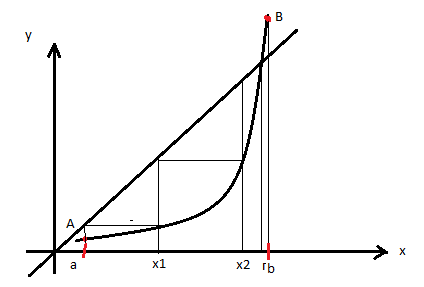
![]()

Достаточные условия сходимости метода простой итерации (теоремы, оценки погрешностей).
Теорема сходимости:
Пусть существует
функция
![]() определена и дифференцируема на отрезке
[a,b].
Причем все значения функции
определена и дифференцируема на отрезке
[a,b].
Причем все значения функции
![]() принадлежат
отрезку [a,b],
тогда если существует правильная дробь
0<q<1
такая что
принадлежат
отрезку [a,b],
тогда если существует правильная дробь
0<q<1
такая что
![]() для
для![]() гдеn=0,1,2…
сходятся независимо от начального
приближения
гдеn=0,1,2…
сходятся независимо от начального
приближения
![]() ,
причем предельное значение
,
причем предельное значение![]() и этот корень единственный.
и этот корень единственный.
Доказательство:
![]() приводя
к эквивалентному виду
приводя
к эквивалентному виду
![]()
![]()
![]()
Обозначим за q=sup![]()

Последовательность приближений хn есть частичные суммы Sn+1 ряда 4
S2=x1
S3=x2……
Sn+1=xn
Члены ряда 4 по абсолютной величине начиная с 3, меньше членов арифметической прогрессии со значениями 0<q<1, q;q2;q3;…;qn.
Геометрическая
прогрессия является сходящейся, значит
существует
![]()
В силу непрерывности
![]() можно
записать
можно
записать![]() ,
значит этот корень уравнения (2).
,
значит этот корень уравнения (2).
Докажем единственность:
Пусть существует
![]() которая
является корнем (2)
которая
является корнем (2)
![]() ,
найдем
,
найдем
![]()
с- внутренняя точка
отрезка [a,b].
![]()
![]()
Замечание 1:
Константа q – носит название константы Липшиця.
Наша теорема справедлива, если функция
 будет
определена и дифференцируема на
интервале (-
будет
определена и дифференцируема на
интервале (- ,
+
,
+ ),
но лишь в том случае, когда константа
Липшиця
),
но лишь в том случае, когда константа
Липшиця .
.В условиях теоремы метод итерации сходится для любого х0
 [a,b]
благодаря чему он является
самоисправляющийся, т.е. отдельные
ошибки в вычислениях не влияют на
результат.
[a,b]
благодаря чему он является
самоисправляющийся, т.е. отдельные
ошибки в вычислениях не влияют на
результат.
Оценка приближений
Рассмотрим модуль
разности
![]() известно,
что модуль суммы
известно,
что модуль суммы Процесс
итерации сходится тем быстрее чем меньшеq.
Процесс
итерации сходится тем быстрее чем меньшеq.
При желании можно
вывести
![]()
Замечание: Если
q=1\2,
то
![]()
Процесс итерации
следует продолжать до тех пор пока 2
последующих приближений не будет
удовлетворять условию
![]()
Докажем, что каждое из приближений xn располагается ближе к корню.
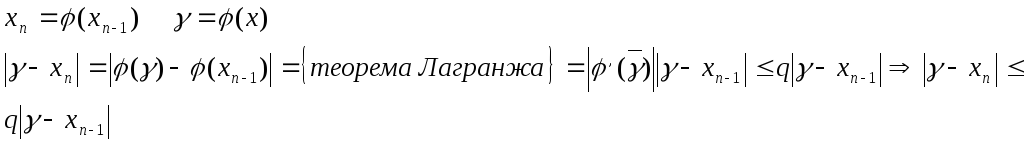
т.е. последовательность
приближений изменяется монотонно и
каждое последующее приближение
n![]() располагается
ближе к корню
располагается
ближе к корню
![]() .
.
Теорема сходимости 2:
Пусть
![]() определена
и дифференцируема на некотором отрезке
[a,b],
причем х=
определена
и дифференцируема на некотором отрезке
[a,b],
причем х=![]() имеет корень
имеет корень![]() лежащий
в более узком отрезке
лежащий
в более узком отрезке![]() ,
где
,
где![]() тогда
если:
тогда
если:

 ,
то все последующие приближения будут
принадлежать интервалу [a,b],
и процесс итерации будет сходится к
единственному корню уравнения х=
,
то все последующие приближения будут
принадлежать интервалу [a,b],
и процесс итерации будет сходится к
единственному корню уравнения х= ,
причем будет выполняться оценка (5).
,
причем будет выполняться оценка (5).
