
АГ ПЗ 1-35 (полный вариант)
.pdf
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 14, с.20
то x |
5 |
1 (x 1)(x |
2 |
|
2cos |
2 |
2 |
|
2cos |
|
||
|
|
|
5 |
x 1)(x |
|
|
5 |
x 1) . |
||||
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: x |
5 |
1 (x 1)(x |
2 |
2 |
|
2 |
2 |
2 |
|
|
||
|
|
cos |
5 |
x 1)(x |
|
cos |
5 |
x 1) . |
||||
|
|
|
|
|
|
|
|
|
|
|
||
Пример 6. Найти все корни 3-й степени из 1, изобразить их на комплексной плоскости, и построить для них таблицу умножения. Решение. Обозначим для простоты
1 cos 23 sin 23 12 i 23 . Тогда 3 1 {1, , 2 }, где 3 1.
Изобразим все корни третьей степени из 1 на комплексной плоскости. Т.к. их модуль равен 1, то все они лежат на тригонометрической (т.е. единичной) окружности:
у
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
o 1 |
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
|
|||
Здесь, |
arg 2 |
, |
arg 2 |
|
4 . Заполняем таблицу Кэли (таблицу ум- |
|||||||||
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
ножения): |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
||
|
|
|
|
|
|
2 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|||||||
Здесь, |
2 2 4 |
3 1 . |
|
|
|
|
|
|||||||
Ответ: |
3 1 {1, |
1 |
i |
3 |
} , рисунок 4 и таблица 1. |
|||||||||
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
13 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 14, с.20
Пример 7. Найти значение функции Эйлера (n) для чисел: а) n 15 ;
б) n 7 ; в) n 18 .
Решение. а) 15 3 5 – разложение числа в произведение простых множителей. Применяя формулу вычисления функции Эйлера, получаем
(15) |
15 |
|
|
1 |
|
|
1 |
|
2 4 8 . |
1 |
3 |
1 |
5 |
|
|||||
|
|
|
|
|
|
|
|
б) Если число n p – простое число, то (p) p 1 . Отсюда следует,
что (7) 6 .
в) Функция Эйлера обладает свойством мультипликативности, т.е. ес-
ли числа n и m взаимно простые, то
(n m) (n) (m) .
Отсюда следует, что (18) (2) (9) (2 1) (9) (9) .
Воспользуемся формулой
(p2 ) p2 p ,
где р – простое число. Получаем (9) (32 ) 32 3 6 .
Ответ: (15) 8, (7) 6, (18) 6 .
Пример 8. Найти все первообразные корни 12-й степени из 1 и записать круговой многочлен Ф12 (x) .
Решение. Во-первых, число первообразных корней 12-й степени из 1 равно
(12) (22 ) (3) (22 2)(3 1) 4 .
Во-вторых, выпишем все корни 12-й степени из 1: { k },
где k {0,1,...,11},
cos |
2 |
isin |
2 |
cos |
|
isin |
|
|
3 |
i |
1 . |
|||||||||||||||||
12 |
12 |
|
6 |
6 |
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
Первообразными |
|
корнями |
являются |
корни |
k , |
|
для которых |
|||||||||||||||||||||
н.о.д.(k,12) 1, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
i |
|
|
|
|
3 |
|
|
i |
|
|
|
|
5 |
|
|
7 |
|
|
5 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
, |
|
, |
|
|
|
|
|
, |
|
или |
|
|
|
|
|
, |
|
|
|
|
|
, |
||||||
|
|
|
|
|
2 |
2 |
|
2 |
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 14, с.20
где 5 cos 56 isin 56 23 i 12 . Вычисляем круговой многочлен Ф12 (x) (x )(x )(x 5 )(x 5 )
(x2 ( )x )(x2 ( 5 5 )x 5 5 )
|
(x2 |
|
3x 1)(x2 |
|
3x 1) (x2 1)2 ( |
3x)2 |
|||||
|
|
|
|
|
|
x4 x2 1. |
|
||||
|
3 |
|
|
|
|
|
4 |
|
2 |
|
|
|
|
i |
|
|
|
|
|
||||
Ответ: |
|
|
|
|
, |
Ф12 (x) x |
|
x |
|
1. |
|
2 |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Пример 9. Найти значение функции Мёбиуса (n) для чисел: а)
n 15 ; б) n 7 ; в) n 18 .
Решение. Ответ следует из определения функции Мёбиуса.
Ответ: (15) ( 1)2 1, (7) 1, (18) 0 .
Пример 10. Разложить степенной двучлен x12 1 на неприводимые множители над полем рациональных чисел.
Решение. 1-й способ. Воспользуемся формулой xn 1 Фd1 (x)Фd2 (x)...Фd (x) ,
где d1 , d2 ,...,d – все делители (положительные) числа n. Делители
числа 12 суть числа: 1, 2, 3, 4, 6, 12, следовательно,
x12 1 Ф1 (x)Ф2 (x)Ф3 (x)Ф4 (x)Ф6 (x)Ф12 (x) .
По этой же формуле, имеем
x1 Ф1 (x) ,
x2 1 Ф1 (x)Ф2 (x) (x 1)Ф2 (x) ,
откуда находим Ф2 (x) x 1. Далее,
x3 1 Ф1 (x)Ф3 (x) (x 1)Ф3 (x) ,
откуда
Ф3 (x) x3 1 x2 x 1 .
x1
Далее,
x4 1 Ф1 (x)Ф2 (x)Ф4 (x) (x 1)(x 1)Ф4 (x) ,
15
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 14, с.20
Ф |
4 |
(x) |
|
x4 1 |
|
(x2 1)(x2 1) x2 1. |
||||||||||||
(x 1)(x 1) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
|
||||||
И, наконец, |
|
|
|
x6 1 Ф (x)Ф |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
(x)Ф |
3 |
(x)Ф |
6 |
(x) |
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
(x 1)(x 1)(x2 x 1)Ф6 (x) (x 1)(x3 1)Ф6 (x) , |
||||||||||||||||||
|
Ф |
6 |
(x) |
|
x6 1 |
|
|
|
|
x3 1 |
x2 x 1. |
|||||||
|
(x3 1)(x 1) |
|
||||||||||||||||
|
|
|
|
|
|
|
x 1 |
|
|
|||||||||
Многочлен Ф (x) x4 |
x2 1 найден в примере 8. В результате по- |
|||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лучаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x12 1 (x 1)(x 1)(x2 x 1)(x2 |
1)(x2 |
x 1)(x4 x2 1) . |
||||||||||||||||
2-й способ. Воспользуемся формулой
|
|
|
n |
|
|
|
n |
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
d |
d |
|
d |
d |
|
|
d |
|
|||||||
Фn (x) (x 1 |
1) |
1 |
(x |
2 |
1) 2 |
...(x |
|
1) , |
||||||||
где d1 , d2 ,...,d – все делители числа n. Получаем: |
|
|
|
|
|
|||||||||||
Ф (x) (x 1) (1) x 1, |
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1) x 1, |
|||||
|
|
|
|
|
|
|
||||||||||
Ф2 (x) (x 1) |
1 (x2 |
1) |
2 |
(x 1) 1 (x2 |
|
|||||||||||
Ф3 (x) (x 1) (3) (x3 1) (1) |
(x 1) 1 (x3 |
1) x2 |
x 1, |
|||||||||||||
Ф4 (x) (x 1) (4) (x2 1) (2) (x4 |
1) (1) |
(x 1)0 (x2 |
1) 1 (x4 1) x2 1 |
|||||||||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
Ф6 (x) (x 1) (6) (x2 1) (3) (x3 1) (2) (x6 1) (1)
(x 1)(x2 1) 1 (x3 1) 1 (x6 1) x2 x 1.
Ф12 (x) (x 1) (12) (x2 1) (6) (x3 1) (4) (x4 1) (3)(x6 1) (2) (x12 1) (1) (x 1)0 (x2 1)(x3 1)0
(x4 1) 1 (x6 1) 1 (x12 1) |
(x2 1)(x12 1) |
|
x6 |
1 |
|
|
|
(x4 1)(x6 1) |
x2 |
1 |
|||||
|
|
|
|||||
(x2 )3 1 x4 x2 1.
x2 1
Ответ: x12 1 (x 1)(x 1)(x2 x 1)(x2 1)(x2 x 1)(x4 x2 1) .
16
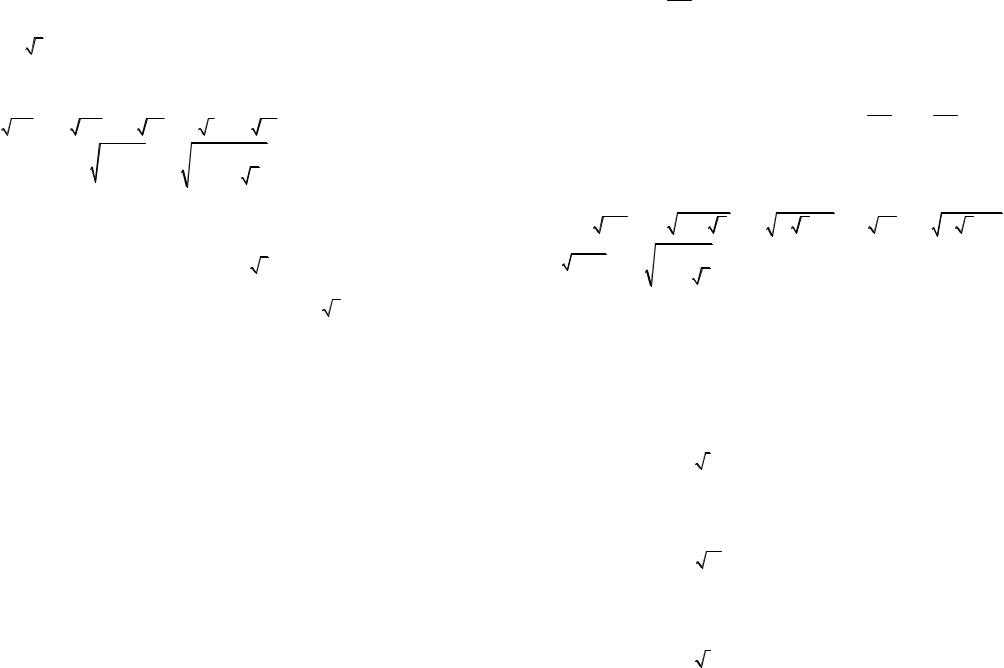
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 14, с.20
п.4. Задачи Задачи для аудиторного решения 14
1.Выпишите формулу корней n-й степени из комплексного числа.
2.Дано: n z . а) Найдите | z | и arg z ; б) Подставьте вычисленные дан-
ные в формулу корней n-й степени из комплексного числа z и запишите по отдельности каждый корень в тригонометрической форме; в) изобразите все найденные корни на комплексной плоскости.
а) 3 8i ; б) |
3 27i ; в) 3 27 ; |
г) |
6 1 ; |
д) |
6 1 . |
||||
3. Вычислить: |
а) |
3 8 24i |
; б) |
4 |
|
|
32 |
|
. |
|
i |
3) |
|||||||
|
|
3 i |
|
|
9(1 |
|
|||
4.Разложить на линейные множители многочлен: а) x6 1; б) x8 1 .
5.Разложите данные многочлены на неприводимые над R: а) x6 1;
б) x8 1 .
6. Найдите сумму таких чисел z, что z4 |
3 i . Укажите одно из этих |
чисел. |
|
7. Найдите произведение таких чисел z, что z4 1 i 3 . Укажите одно из этих чисел.
Задачи повышенного уровня сложности 14
8.Составьте таблицу умножения для группы корней 5-й степени из 1.
9.Разложить на линейные множители многочлен x6 64 .
10.Разложите многочлен x8 256 на неприводимые над R множители.
11.Разложите многочлен x4 4 на два квадратных трехчлена с действительными коэффициентами.
12.Разложить многочлен x4 x3 x2 x 1 на два квадратных трехчлена с действительными коэффициентами.
13.Вычислите значение функции Эйлера (720) .
14.Вычислите значение функции Мёбиуса (840) .
15.Найдите степень кругового многочлена Ф16800 (x) .
16.Найдите круговой многочлен Ф9 (x) .
17.Разложите многочлен x9 1 на неприводимые над Q.
18.Не вычисляя корней уравнения x2 x 1 0 , докажите, что его корни являются корнями 3-й степени из 1.
17
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 14, с.20
19.Вычислите z142 z1421 , если z 1z 1.
20.Докажите что сумма всех корней n-й степени из 1 равна нулю.
21.Найдите сумму всех первообразных корней р-й степени из 1, если
р– простое число.
22.Найдите сумму 100 членов геометрической прогрессии, первый
член которой равен 1, а знаменатель равен cos100 isin 100 . Ответ дайте в тригонометрической форме.
Домашнее задание 14. Корни из комплексных чисел
1. Найдите все данные корни и изобразите их на комплексной плоско-
сти: а) 4 1 i ; |
б) |
6 1 3i ; в) 3 4( |
3 i) ; |
г) 4 4 ; д) 4 8( |
3i 1) ; |
|
е) 3 1 i ; ж) |
4 |
18 |
. |
|
|
|
1 i 3 |
|
|
|
|||
2.Разложить на линейные множители многочлен: а) x3 1; б) x4 16 .
3.Разложите многочлен x10 1 на неприводимые над R.
4*. Найдите круговой многочлен Ф10 (x) и разложите многочлен x10 1 на неприводимые над Q.
Самостоятельная работа 14
Вариант1.
1.Определение корня n-й степени из комплексного числа.
2.Вычислить все корни 3 i , записать их в тригонометрической форме
иотметить на комплексной плоскости.
3.Разложите многочлен x3 1 на линейные множители.
Вариант2.
1.Определение первообразного корня n-й степени из 1.
2.Вычислить все корни 3 i , записать их в тригонометрической форме и отметить на комплексной плоскости.
3.Разложите многочлен x3 1 на линейные множители.
Вариант3.
1.Определение функции Эйлера.
2.Вычислить все корни 4 i , записать их в тригонометрической форме
иотметить на комплексной плоскости.
18

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 14, с.20
3. Разложите многочлен x4 16 на линейные множители. Вариант4.
1.Определение кругового многочлена Фn (x) .
2.Вычислить все корни 4 i , записать их в тригонометрической форме и отметить на комплексной плоскости.
3.Разложите многочлен x4 1 на линейные множители.
п.5. Вопросы и задачи для самоконтроля 14 Обозначения
1.Обозначение корней n-й степени из комплексного числа.
2.Обозначение корней n-й степени из 1.
3.Обозначение функции Эйлера.
4.Обозначение функции Мёбиуса.
5.Обозначение числа положительных делителей натурального числа.
6.Обозначение кругового многочлена.
Определения
1.Определение корня n-й степени из комплексного числа.
2.Определение разложимого и неприводимого (неразложимого) над полем многочлена.
3.Определение первообразного корня n-й степени из 1.
4.Определение кругового многочлена.
5.Определение функции Эйлера.
6.Определение функции Мёбиуса.
Теоремы
1.Формула корней n-й степени из комплексного числа.
2.Формула корней n-й степени из 1.
3.Теорема о разложении степенного двучлена на линейные множители.
4.Разложение степенного двучлена на линейные и квадратичные множители над полем действительных чисел.
5.Основная теорема алгебры и её следствие о количестве корней многочлена.
6.Неприводимые многочлены над полем комплексных чисел и над полем действительных чисел.
7.Необходимый и достаточный признак первообразного корня из 1.
8.Свойства кругового многочлена.
19
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 14, с.20
9.Разложение степенного двучлена на неприводимые множители над полем рациональных чисел.
10.Вычисление кругового многочлена.
Тест 14
1.Найдите все корни 3 i , запишите их в тригонометрической форме, и изобразите на комплексной плоскости, указав их модули и аргументы.
2.Найдите все корни 4 16 , запишите их в тригонометрической форме, и изобразите на комплексной плоскости, указав их модули и аргументы.
3. Найдите все корни 3 1 , запишите их в тригонометрической форме, и изобразите на комплексной плоскости, указав их модули и аргументы.
4.Разложите на линейные множители многочлен x3 1 .
5.Разложите степенной двучлен x4 1 на линейные множители.
6.Разложите степенной двучлен x4 1 на неприводимые множители над полем действительных чисел.
7.Найдите все первообразные корни 4-й степени из 1 и составьте для них таблицу умножения.
8.Найдите число первообразных корней 5-й степени из 1.
9.Разложите степенной двучлен x5 1 на неприводимые множители над полем рациональных чисел.
10.Найдите круговой многочлен Ф10 (x) .
20

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
Практическое занятие 15 Скалярное произведение векторов
Краткое содержание: определение и простейшие свойства скалярного произведения, свойство линейности скалярного произведения, скалярное произведение векторов в координатной форме, вычисление модуля вектора и угла между векторами, физический смысл скалярного произведения.
п.1. Теория п.1.1. Определение и свойства скалярного произведения
Определение. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними, и обозначается
a b | a | | b | cos(a ^ b) .
Определение. Скалярное произведение вектора на себя называется его скалярным квадратом, и обозначается
a2 a a .
Теорема. (Простейшие свойства скалярного произведения.)
1) Скалярное произведение подчиняется закону коммутативности:
|
|
|
|
|
|
|
|
|
|
|
|
. |
a, b VS |
a |
b |
b |
a |
||||||||
2) Скалярное произведение двух векторов равно нулю тогда и только тогда, когда хотя бы один из векторов нулевой или векторы ортогональны:
a b 0 (a 0) (b 0) (a b) .
3). Скалярный квадрат вектора равен квадрату его модуля: a2 | a |2 .
4). Скалярное произведение двух векторов равно произведению модуля одного из векторов на проекцию на него другого вектора:
a b | b | прb a | a | прa b .
Теорема. (Свойство линейности скалярного произведения.)
1) Скалярное произведение дистрибутивно относительно сложения векторов (свойство аддитивности по каждому из двух аргументов):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, b, c VS |
(a |
b) c a c b c , a (b c) a b a c . |
|||||||||||||||||||||||||||||||||
2) Скалярный множитель можно выносить за знак скалярного произ-
1
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
ведения (свойство однородности по каждому из двух аргументов):
a, b VS , R ( a) b a ( b) (a b) .
п.1.2. Скалярное произведение векторов в координатной форме Теорема. (Скалярное произведение векторов в координатной форме.) Скалярное произведение векторов равно сумме произведений соответствующих координат, т.е. если
a x1 i y1 j z1 k (x1 , y1 , z1 ) , b x2 i y2 j z2 k (x2 , y2 , z2 ) ,
то
a b x1x2 y1y2 z1z2 .
Следствие 1. Модуль вектора равен корню квадратному из суммы квадратов его координат, т.е. если a (x, y,z) , то
| a | x2 y2 z2 .
Следствие 2. Если векторы заданы в координатной форме,
a (x1 , y1 ,z1 ), b (x2 , y2 ,z2 ) ,
то угол между ними можно вычислить по формуле:
|
|
|
|
|
|
|
a |
|
b |
|
|
|
x1x2 y1y2 z1z2 |
||||
(a ^ b) arccos |
arccos |
||||||||||||||||
|
|
|
|
|
|
. |
|||||||||||
| |
|
|
| | |
|
|
| |
x12 y12 z12 x22 y22 z22 |
||||||||||
a |
b |
||||||||||||||||
Следствие 3. Если векторы заданы в координатной форме
a (x1 , y1 ,z1 ), b (x2 , y2 ,z2 ) , то проекцию вектора на вектор можно вычислить по формуле:
пр |
|
|
|
|
a |
|
b |
|
|
x1y1 x2 y2 z1z2 |
. |
|
|
|
a |
||||||||||
|
|
|
|
|
|
|
||||||
b |
||||||||||||
|
|
|
| b | |
|
x22 y22 z22 |
|||||||
|
|
|
|
|
|
|||||||
Физический смысл скалярного произведения
Работа А, производимая вектором силы F при перемещении матери-
альной точки вдоль вектора перемещения s равна их скалярному произведению:
A F s .
2

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
п.2. Список задач Список №1
1.Вычислить скалярное произведение двух векторов, если известны их модули и угол между ними.
2.Найти скалярный квадрат вектора, если известен его модуль.
3.Найти модуль вектора, если известен его скалярный квадрат.
4.Найти скалярный квадрат и модуль суммы двух векторов, если известны модули слагаемых и угол между ними.
5.Зная координаты двух векторов, вычислить их скалярное произведение.
6.Найти скалярный квадрат вектора и его модуль, если известны его координаты.
7.Зная координаты двух векторов, вычислить проекцию одного вектора на другой.
8.Зная координаты двух векторов, вычислить угол между ними.
9.Проверить ортогональность векторов.
10.Вычислить работу, совершаемую вектором силы вдоль вектора перемещения материальной точки.
Список № 2
1.Задачи планиметрии и стереометрии, решаемые с помощью метода координат, и с применением скалярного произведения.
п.3. Примеры
Пример 1. Найти скалярное произведение векторов a и b , если
| a | 2, | b | 5, (a ^ b) 5 . |
|
|
6 |
|
|
Решение. По определению скалярного произведения |
||
a b | a | | b | cos(a ^ b) 2 5 cos |
5 |
5 3 . |
|
6 |
|
Ответ: 5 3 .
Пример 2. Найти скалярный квадрат вектора a , если его модуль равен 3.
Решение. Воспользуемся свойством скалярного произведения, что скалярный квадрат вектора равен квадрату его модуля:
a2 | a |2 32 9 . Ответ: 9.
3
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
Пример 3. Найти модуль вектора, если его скалярный квадрат равен
18.
Решение. Воспользуемся свойством скалярного произведения, что
скалярный квадрат вектора равен квадрату его модуля: a2 | a |2 18 . Отсюда находим модуль вектора.
Ответ: 3 2 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 . |
Пример 4. Найти (a |
b)2 |
и | a b | , если | a | 2, | b | |
2 , (a ^ b) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
Решение. Воспользуемся свойством линейности скалярного произведения, и найдем скалярный квадрат суммы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
(a b) |
|
a |
2a b |
b |
| a | |
2 | a | | b | cos |
| b | |
2 . |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
||||||||||||||||||||||||||||||||||||||||
Отсюда, |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a |
b |
(a |
b)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2, | |
|
|
|
| |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Ответ: (a |
b)2 |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Пример |
5. |
|
|
|
Найти |
|
|
скалярное |
|
произведение |
|
векторов |
||||||||||||||||||||||||||||||||||||
|
|
( 2;5; 3), |
|
(1;2;3) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Решение. Воспользуемся формулой вычисления скалярного произведения векторов, заданных в координатной форме:
a b x1x2 y1y2 z1z2 2 10 9 1 .
Ответ: –1.
Пример 6. Найти скалярный квадрат вектора a ( 2;6; 3) , и его мо-
дуль.
Решение. Вычисляем скалярный квадрат данного вектора, используя формулу скалярного произведения векторов, заданных в координатной форме:
a2 a a x1x1 y1y1 z1z1 x12 y12 z12 4 36 9 49 .
По свойству скалярного произведения, модуль вектора равен квадратному корню из его скалярного квадрата:
| a | a2 49 7 .
Ответ: 7.
4
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
Пример 7. Найти проекцию вектора a (1;2;4) на вектор
b ( 2;6; 3) .
Решение. Воспользуемся формулой вычисления проекции вектора на вектор, если векторы заданы в координатной форме:
|
пр |
|
|
|
|
a |
|
b |
|
|
x1y1 x2 y2 z1z2 |
2 12 12 2 . |
|||||
|
|
|
a |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
b |
||||||||||||||||
|
|
|
|
| b | |
|
x22 y22 z22 |
|
|
4 36 9 |
7 |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
Ответ: |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 8. Найти угол между векторами |
|
( 3;0;4) |
и |
|
( 2;6; 3) . |
||||||||||||
a |
b |
||||||||||||||||
Решение. Вычисляем скалярное произведение данных векторов и их модули:
a b 6 0 12 6, | a | 5, | b | 7 .
По формуле угла между векторами, находим
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
6 |
|
||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
(a ^ b) arccos |
|
|
|
|
|
|
|
|
|
arccos |
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
35 |
||||||||
|
|
|
|
|
|
|
|
| a | | b | |
|
|
|
|||||||||
Ответ: |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
arccos |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 9. Выяснить, ортогональны ли векторы a ( 2;6;4) и
b (1; 3;5) .
Решение. Два ненулевых вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю. Вычисляем скалярное произведение данных векторов:
a b 2 18 20 0 .
Ответ: данные векторы ортогональные.
Пример 10. Вычислить, какую работу производит сила f (3; 5; 2) , когда ее точка приложения перемещается из начала в конец вектора s (2; 5; 7) .
Решение. Работа равна скалярному произведению вектора силы на
вектор перемещения: A f s 6 25 14 17 . Ответ: 17.
5
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
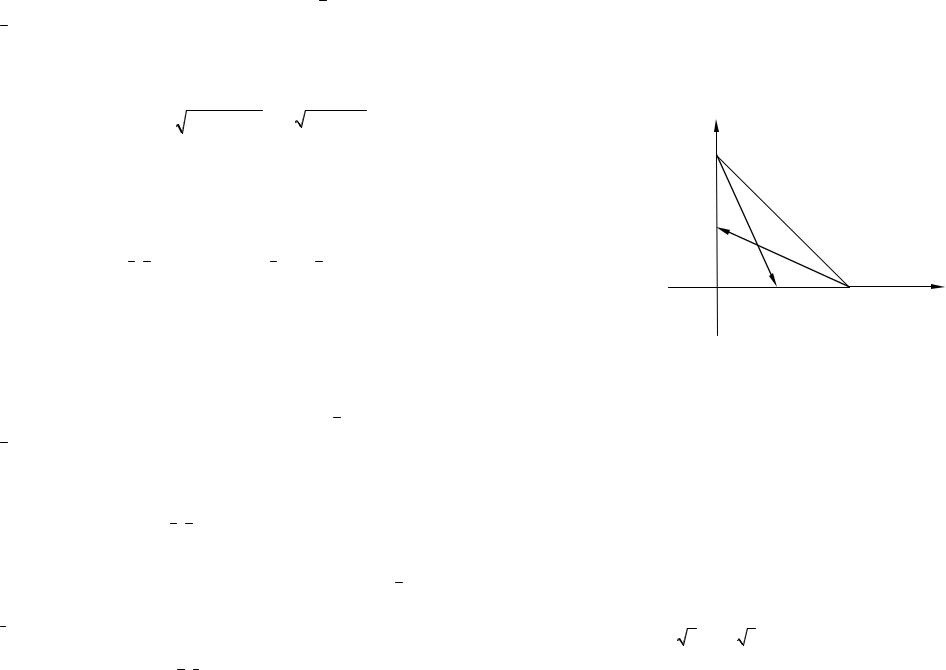
Пример 11. Вычислить тупой угол, образованный медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника.
Решение. Обозначим длины катетов данного равнобедренного прямоугольного треугольника через а, и введем систему координат как на рисунке 1.
у
В(а)
a |
|
|
|
M |
|
|
|
2 |
|
|
|
|
|
|
х |
О |
a |
|
А(а) |
|
N |
|
|
|
2 |
|
|
Рис. 1
Искомый угол равен углу между векторами
|
|
a; |
a |
|
1; |
1 |
|
|
a |
|
1 |
|
||||
|
|
|||||||||||||||
AM |
2 |
|
a |
2 |
|
и BN |
2 |
; a |
a |
2 |
; 1 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
По формуле угла между векторами, получаем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AM |
|
BN |
|
|
|
a2 |
|
4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
cos(AM ^ BN) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
| AM | | BN | |
a |
2 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: arccos |
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
п.4. Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задачи для аудиторного решения 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
1. Зная, что | |
|
|
| |
2, | |
|
| 3 , вычислить скалярное произведение век- |
|||||||||||||||||||||||||||||
a |
b |
||||||||||||||||||||||||||||||||||
торов |
|
и |
|
, если угол между ними равен: |
|
а) |
2 |
; б) |
3 |
; |
в) |
|
; |
||||||||||||||||||||||
a |
b |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
г) 2 ; д) 56 ; е) 3 ; ё) 4 .
2.Найти скалярный квадрат вектора a , если его модуль равен 3 4 .
3.Найти модуль вектора, если известно, что его скалярный квадрат равен 3 4 .
4. |
Дано: | |
|
| 2, | |
|
| |
|
|
|
|
|
|
. Найти: а) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
a |
b |
2, (a |
^ b) |
(a |
b)2 ; |
б) | a b | ; |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
в) (3a |
2b)(a 2b) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
5. |
Даны векторы |
|
(4; 2; 4), |
|
(6; 3; 2) . Вычислить их скаляр- |
||||||||||||||||||||||||||||
a |
b |
||||||||||||||||||||||||||||||||
|
ное произведение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
6.Вычислить скалярный квадрат вектора a (4; 2; 4) и его модуль.
7.Вычислить проекцию вектора a (5; 2; 5) на вектор b (2; 1; 2) .
8. Вычислить косинус угла, образованного векторами a (2; 4; 4) и
b( 3; 2; 6) .
9.Дано, что | a | 3, | b | 5 . Определить, при каком значении векторы a b, a b будут ортогональны.
10.Найти работу производимую силой f (3; 2; 5) , когда её точка
приложения, двигаясь прямолинейно, перемещается из точки А(2; – 3; 5) в точку В(3; –2; –1).
11. Даны вершины треугольника А(3; 2; –3), В(5; 1; –1) и С(1; –2; 1).
Найти его внешний угол при вершине А.
12. |
Даны три вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a |
3i 6j |
k, b i 4j 5k и |
c 3i 4j 12k . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вычислить прс (a |
b) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Задачи повышенного уровня сложности 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
13. |
Векторы |
|
и |
|
образуют угол . Зная, |
что | |
|
| |
|
3 , | |
|
| 1, вы- |
|||||||||||||||||||
a |
b |
a |
|
b |
|||||||||||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
числить угол между векторами p a b и q a b .
14. Даны две точки А(3; –4; –2), В(2; 5; –2). Найти проекцию вектора AB на ось, составляющую с координатными осями углы
60o , 120o , а угол – тупой.
15.Найти проекцию вектора a (4; 3; 2) на ось, если она составляет
7
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
скоординатными осями равные острые углы.
16.Вектор x коллинеарный вектору a (6; 8; 7,5) образует острый
угол с осью Oz. Зная, что | x | 50 , найти его координаты.
17.Найти угол между медианой и биссектрисой, проведенными из вершины прямого угла треугольника, если его катеты относятся друг к другу как m : n.
18.Пусть АBCD – правильный тетраэдр с ребром равным 1, О – центр описанной около него сферы. Введите, удобным для вас образом,
ПДСК Охуz и найдите: а) координаты вектора OA , его модуль и направляющие косинусы; б) косинус угла между ребром АВ и радиусом ОА.
Домашнее задание 15. Скалярное произведение векторов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Векторы a и b ортогональны, вектор c образует с ними углы, рав- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ные . Зная, |
что | |
|
|
| 3, | |
|
|
|
| 5, | |
|
|
| 8 , вычислить: а) |
|
|
|
; б) |
|
|
|
; |
|||||||||||||||||||||||||||||||||
|
a |
b |
c |
a |
b |
b |
c |
||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
2 ; |
|
|
|
|
2 ; е) |
|
2 ; ё) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
в) |
|
|
|
; г) |
|
|
д) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
a |
c |
a |
b |
c |
(a |
2b |
3c)2 . |
|||||||||||||||||||||||||||||||||||||||||||||
2. |
Векторы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
a, b, c , попарно образуют друг с другом углы, каждый из |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
которых равен 60o . Зная, что |
|
|
|
| |
|
| 4, | |
|
| 2 , | |
|
| 6 , определить |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
b |
c |
|||||||||||||||||||||||||||||||||||||||||||||||
|
модуль вектора |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
p |
a |
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
3.Даны вершины треугольника А(–1; –2; 4), В(–4; –2; 0) и С(3; –2; 1).
Найдите его внутренний угол при вершине В и расстояние от вершины В до основания высоты, опущенной из вершины А на сторо-
ну ВС. (Указание: найдите | прBC BA | .)
4. Даны два вектора a (3; 1; 5) и b (1; 2; 3) . Найдите вектор c при условии, что он перпендикулярен к оси Oz и удовлетворяет условиям: c a 9, c b 4 . (Указание: положите c (x, y,z) и решите систему уравнений: c a 9, c b 4, c k 0 , где k – орт оси Oz.
Самостоятельная работа 15
Вариант 1.
1. Определение скалярного произведения двух векторов. 2. Вычислить скалярный квадрат вектора a , если | a | 3 .
8

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
3. |
Найти модуль суммы векторов |
|
и |
|
|
|
, если | |
|
| | |
|
|
| |
3 |
|
, а угол ме- |
|||||||||||||||
a |
b |
a |
b |
|||||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||||||
|
жду ними равен 30o . |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
Вариант 2. |
|
|
|
|
|
|||||||||||||||||||||||||
1. Определение скалярного квадрата вектора. |
|
|
|
|
|
|||||||||||||||||||||||||
2. |
Вычислить скалярное произведение |
|
|
|
|
, если | |
|
|
| |
3 , модуль век- |
||||||||||||||||||||
a |
b |
a |
||||||||||||||||||||||||||||
|
тора |
|
в 2 раза больше и угол между ними равен 150o . |
|
|
|||||||||||||||||||||||||
|
b |
2 |
|
|||||||||||||||||||||||||||
3. |
Найти модуль разности векторов |
|
и |
|
, если | |
|
| | |
|
| |
, а угол |
||||||||||||||||||||
a |
b |
a |
b |
|||||||||||||||||||||||||||
3 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
между ними равен 150o . Вариант 3.
1.Формула угла между векторами, заданными в координатной форме.
2.Вычислить модуль вектора a , если скалярный квадрат вектора
|
1 |
|
|
равен |
3 4 . |
|
|
|
|
|
|
|
|
|
|
||||||
a |
|
|
|
|
|
|
|||||||||||||||
3 |
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. Найти | |
|
|
3 |
|
| , если | |
|
| | |
|
| |
3 |
|
|
|
|
|
||||||
a |
b |
a |
b |
, (a |
^ b) 120o . |
||||||||||||||||
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вариант 4.
1.Формула проекции вектора на вектор, если векторы заданы в координатной форме.
2. Вычислить скалярное произведение векторов |
a |
и |
b |
, если | |
a |
| 3 , |
||||||||||||||||||
модуль вектора |
|
на 3 больше и угол между ними равен 150o . |
||||||||||||||||||||||
b |
||||||||||||||||||||||||
3. Найти | |
|
|
3 |
|
| , если | |
|
| | |
|
| |
2 |
|
|
|
|
|
|||||||||
a |
b |
a |
b |
, (a |
^ b) 135o . |
|||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
п.5. Вопросы и задачи для самоконтроля 15 Обозначения
1.Обозначение скалярного произведения.
2.Обозначение скалярного квадрата вектора.
Определения
1.Определение скалярного произведения.
2.Определение скалярного квадрата вектора.
9
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 15, с.10
Теоремы
1.Простейшие свойства скалярного произведения.
2.Свойство линейности скалярного произведения.
3.Формула скалярного произведения векторов в координатной форме.
4.Формула скалярного квадрата вектора.
5.Формула модуля вектора.
6.Формула угла между векторами.
Тест 15 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
, | |
|
| 2, | |
|
| 3. Вычислить: а) |
|
|
|
; б) |
|
2 ; в) |
|
1. Дано: (a |
^ b) |
a |
b |
a |
b |
a |
||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
(a b)2 ; г) | a b | .
2. Вычислите скалярное произведение двух векторов единичной длины, если угол между ними равен 150o .
3.Дан правильный треугольник АВС со стороной 1. Вычислите прCA AB .
4.Пусть BD – высота правильного треугольника АВС со стороной 1.
Найдите скалярное произведение вектора AB на вектор BD .
5.Пусть i и j – орты координатных осей ПДСК Оху. Не пользуясь координатной формой записи, вычислите прi j j . Постройте чертеж.
6. Вычислите скалярное произведение векторов a и b , если a (1; 2; 2), b (2; 2;1) .
7. Даны векторы |
|
(2; 3; 1), |
|
(1; 3; 2) . Вычислить: а) |
|
|
|
|
|
||||
a |
b |
(a |
b)2 ; |
||||||||||
б) | |
|
|
|
| . |
|
|
|
|
|
||||
a |
b |
|
|
|
|
|
|||||||
8. Вычислить косинус угла между векторами a (2; 4; 4) и
|
b |
( 3; 2; 6) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9. |
|
|
|
Вычислите |
проекцию |
вектора |
|
|
|
на вектор |
|
, если |
|||||||||||||||
|
|
|
a |
b |
|||||||||||||||||||||||
|
|
|
(1; 2; 2), |
|
(6; 7; 6) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
10. |
|
|
|
Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
прс (a |
b) , |
если |
a 3i 6j k , |
b i 4j 5k , |
||||||||||||||||||||
c3i 4j 12k .
11.Вычислите проекцию вектора a (1; 2; 2) на противоположный ему вектор.
10

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
Практическое занятие 16 Векторное произведение
Краткое содержание: определение и простейшие свойства векторного произведения векторов, свойства линейности, вычисление векторного произведения векторов, заданных в координатной форме, применения векторного произведения.
п.1. Теория п.1.1. Определение и свойства векторного произведения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. Векторным произведением вектора a |
на вектор b на- |
|||||||||||||||||
зывается третий вектор, который обозначается |
a |
|
b |
и удовлетворяет |
||||||||||||||
следующим трем условиям: |
|
|
|
|||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|||
a |
b |
a, |
a |
b |
b |
|
|
|
||||||||||
2)тройка векторов {a, b, a b} является правоориентированной;
3)| a b | | a | | b | sin (a ^ b) .
a b
b
S | a | | b | sin
a
b a a b
Рис.1.
Из определения следует, что, если векторы a , b и a b отложить от одной точки, то:
1) вектор a b перпендикулярен плоскости, в которой лежат векторы a и b ;
2)кратчайший поворот вектора a к вектору b происходит против часовой стрелки, если смотреть "сверху", т.е. со стороны вектора a b ;
3)длина вектора a b численно равна площади параллелограмма, построенного на векторах a и b , как на его сторонах.
1
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
Теорема. (Свойства векторного произведения.) 1). Антикоммутативность:
a,b VS , a b b a . 2). Условие коллинеарности векторов:
a || b a b 0 .
3). Модуль векторного произведения численно равен площади парал-
лелограмма, построенного на векторах a и b , как на его сторонах.
Из второго свойства следует, что векторное произведение вектора на самого себя есть нулевой вектор и поэтому не имеет смысла говорить о векторном квадрате вектора. В силу этого свойства, квадрат вектора всегда понимается как скалярный квадрат вектора:
(a)2 a 2 | a |2 .
Теорема. (Свойство линейности векторного произведения.)
Для любых векторов и действительных чисел справедливы следующие равенства:
1)(a1 a2 ) b a1 b a2 b ;
2)( a) b (a b) ;
3)a (b1 b2 ) a b1 a b2 ;
4)a ( b) (a b) .
Замечание. Свойство 1) и 3) этой теоремы можно рассматривать как свойство дистрибутивности векторного произведения векторов относительно их сложения.
Свойство антикоммутативности векторного произведения не позволяет нам пользоваться формулами сокращенного умножения. Например,
(a b) (a b) a a a b b a b b 2(a b) .
Из последнего равенства мы видим, что формула сокращенного умножения, а именно разность квадратов здесь не выполняется. Аналогично не выполняются и другие формулы сокращенного умножения. Так, например,
(a b) (a b) 0 , так как (a b) || (a b) .
2
