Билет 12 Непараметрические методы. Поиск критерия, адекватного задаче исследования.
непараметрические методы в математической статистике, методы непосредственной оценки теоретического распределения вероятностей и тех или иных его общих свойств (симметрии и т.п.) по результатам наблюдений. Название Н. м. подчёркивает их отличие от классических (параметрических) методов, в которых предполагается, что неизвестное теоретическое распределение принадлежит какому-либо семейству, зависящему от конечного числа параметров (например, семейству нормальных распределений, и которые позволяют по результатам наблюдений оценивать неизвестные значения этих параметров и проверять те или иные гипотезы относительно их значений. Разработка Н. м. является в значительной степени заслугой советских учёных.
В качестве примера Н. м. можно привести найденный А. Н. Колмогоровым способ проверки согласованности теоретических и эмпирических распределений (так называемый критерий Колмогорова). Пусть результаты n независимых наблюдений некоторой величины имеют функцию распределения F (x) и пусть Fn (x) обозначает эмпирическую функцию распределения, построенную по этим n наблюдениям, a Dn —наибольшее по абсолютной величине значение разности Fn (x) — F (x). Случайная величина
имеет в случае непрерывности F (x) функцию распределения Kn (λ), не зависящую от F(x) и стремящуюся при безграничном возрастании n к пределу
Отсюда при достаточно больших n, для вероятности pn,λ. Неравенства
получается приближённое выражение
pn,λ ≈ 1 - К (λ). (*)
Функция К (λ) табулирована. Её значения для некоторых А приведены в табл.
Таблица функции К (λ)
----------------------------------------------------------------------------------------------------------------------------------------------------
| λ | 0,57 | 0,71 | 0,83 | 1,02 | 1,36 | 1,63 |
|--------------------------------------------------------------------------------------------------------------------------------------------------|
| К (λ) | 0,10 | 0,30 | 0,50 | 0,75 | 0,95 | 0,99 |
----------------------------------------------------------------------------------------------------------------------------------------------------
Равенство (*) следующим образом используется для проверки гипотезы о том, что наблюдаемая случайная величина имеет функцию распределения F (x): сначала по результатам наблюдений находят значение величины Dn, а затем по формуле (*) вычисляют вероятность получения отклонения Fn от F, большего или равного наблюдённому. Если указанная вероятность достаточно мала, то в соответствии с общими принципами проверки статистических гипотез (см. Статистическая проверка гипотез) проверяемую гипотезу отвергают. В противном случае считают, что результаты опыта не противоречат проверяемой гипотезе. Аналогично проверяется гипотеза о том, получены ли две независимые выборки, объёма n1 и n2 соответственно, из одной и той же генеральной совокупности с непрерывным законом распределения. При этом вместо формулы (*) пользуются тем, что вероятность неравенства
как это было установлено Н. В. Смирновым, имеет пределом К (λ), здесь Dn1, n2 есть наибольшее по абсолютной величине значение разности Fn1 (х) — Fn2 (х).
Другим примером Н. м. могут служить методы проверки гипотезы о том, что теоретическое распределение принадлежит к семейству нормальных распределений. Отметим здесь лишь один из этих методов — так называемый метод выпрямленной диаграммы. Этот метод основывается на следующем замечании. Если случайная величина Х имеет нормальное распределение с параметрами α и σ, то
где Ф-1 — функция, обратная нормальной:
Т. о., график функции у = Ф-1[F (x)] будет в этом случае прямой линией, а график функции у = Ф-1[Fn (x)] — ломаной линией, близкой к этой прямой (см. рис.). Степень близости и служит критерием для проверки гипотезы нормальности распределения F (x).
.
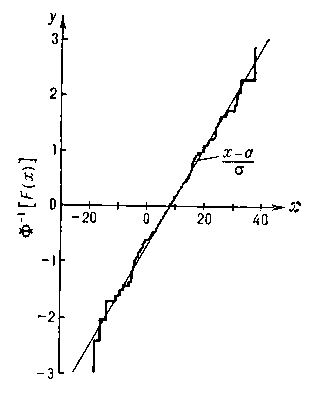Поиск критерия, адекватного задаче исследования.
Параметрические критерии могут оказаться несколько более мощными, чем непараметрические, но только в том случае, если признак измерен по интервальной шкале и нормально распределен. С интервальной шкалой есть определенные проблемы . Лишь с некоторой натяжкой мы можем считать данные, представленные не в стандартизованных оценках, как интервальные. Кроме того, проверка распределения "на нормальность" требует достаточно сложных расчетов, результат которых заранее неизвестен . Может оказаться, что распределение признака отличается от нормального, и нам так или иначе все равно придется обратиться к непараметрическим критериям.
Непараметрические критерии лишены всех этих ограничений и не требуют таких длительных и сложных расчетов. По сравнению с параметрическими критериями они ограничены лишь в одном - с их помощью невозможно оценить взаимодействие двух или более условий или факторов, влияющих на изменение признака. Эту задачу может решить только дисперсионный двухфакторный анализ.
