Номинальная+и+эффективная+ставки+процентов

Номинальная и эффективная ставки процентов

Номинальная процентная ставка наращения

Год – это стандартный промежуток времени начисления процентов. Однако зачастую в финансовых операциях в качестве промежутка наращения процентов используется не год, а, например, месяц, квартал или другой период. В этом случае проценты начисляются m раз в году. В договорах обычно фиксируется не ставка за период, а годовая процентная, которая в этом случае называется номинальной. Сложная процентная ставка наращения является ч а с т н ы м с л у ч а е м номинальной при начислении процентов один раз в году.

Пусть j – номинальная ставка процентов. Проценты за один период начисляются по ставке j / m , а количество начислений равно m n. Наращённая сумма при использовании номинальной процентной ставки наращения определяется по формуле:

Задача 1. Какой величины достигнет долг, равный 20 000 р. через 5.7 года при росте по сложной ставке 14% годовых при начислении процентов раз в году и помесячно?

Решение. По условию i=0.14, P = 20 000, t=5.7. Тогда при начислении процентов раз в году получим S = 20 000(1+0.14)5.7 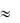42207 р. 31 коп. При начислении процентов помесячно имеем

Дисконтный множитель имеет вид 1/(1+j/m)mn.

Задача 2. Сумма 30 000 р. выплачивается через 2.5 года. Номинальная ставка процентов 16% годовых. Определить современную стоимость при ежеквартальном начислении процентов.

Решение. В условии задачи применен термин «современная стоимость». Этот термин означает денежную сумму, которая эквивалентна размеру платежа, который должен быть получен в будущем. В данном случае требуется найти дисконтированную сумму для S =30 000: фактически ставится вопрос о стоимости этой суммы S, которая должна быть выплачена через 2.5 года, в настоящее время. Используя формулу (2) при j%=16%, m=4, n=2.5, получаем

P = 30 000 (1+0.16/4)–2.5 4 = 30 000 / (1+0.04)10 20266 р. 93 коп.

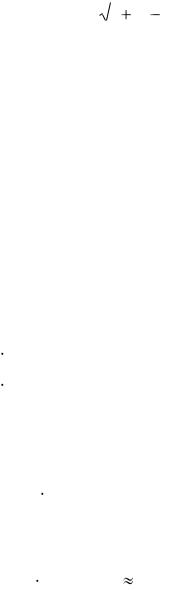
Эффективная процентная ставка наращения

Пусть номинальная годовая ставка процентов равна j и срок ссуды составляет один год. В этом случае при начислении процентов m раз в году по ставке j/m получаем множитель наращения (1+ j/m)m. Пусть теперь проценты начисляются лишь один раз в конце года по некоторой ставке a; множитель наращения имеет вид 1+a. Процентная ставка a является эффективной, если справедливо равенство

Иначе говоря, эффективная ставка процентов – это годовая ставка процентов при начислении раз в году, которая даёт такой же результат, что m-разовое начисление процентов по ставке j/m. Из (3) вытекают равенства, связывающие номинальную и эффективную процентные ставки и наоборот:

(1+a)n = (1+ j/m)m n ,

которое можно истолковать следующим образом: замена в договоре сроком на n лет номинальной ставки j при m-разовом начислении процентов на эффективную ставку a не изменит финансовых обязательств участников, т.е. обе ставки эквивалентны в финансовом отношении.

Задача 3. Номинальная ставка процента при начислении раз в полугодие равна 10%. Определить эффективную ставку.

Решение. Здесь j=0.1, m=2. Тогда a = (1+ j/m)m – 1 = (1+0.1/2)2 – 1 = 0.1025.

Пусть срок ссуды составляет n единичных промежутков. Рассмотрим соотношение эквивалентности между простой процентной ставкой наращения iпр и сложной процентной ставкой iсл. Это соотношение запишем с учетом условия, что начальная и наращённая суммы при применении рассматриваемых ставок одинаковы. Приравняем множители наращения друг к другу:

1+ n iпр = (1 + iсл)n,

откуда iпр = [(1 + iсл)n – 1] / n, iсл = (1 + n iпр)1/n – 1.

Задача 4. Простая процентная ставка депозита равна 10% годовых. Определить доходность в виде сложной годовой процентной ставки в случае: а) срок депозита составляет 0.5 года, б) срок депозита составляет 1.5 года.

Решение.

а) Имеем n=0.5, iпр = 0.1. Тогда iсл = (1 + 0.5 0.1)1/0.5 – 1= 0.1025 > iпр. Тот факт, что получилось iсл > iпр вполне согласуется с тем, что наращение сложных процентов идет медленнее, чем простых процентов, когда длина периода наращения меньше единичного периода.

б) Имеем n=1.5, iпр = 0.1. Тогда iсл = (1 + 1.5 0.1)1/1.5 – 1 0.09765 < iпр. Тот факт, что получилось iсл < iпр вполне согласуется с тем, что наращение сложных процентов идет быстрее, чем простых процентов, когда длина периода наращения больше единичного периода.

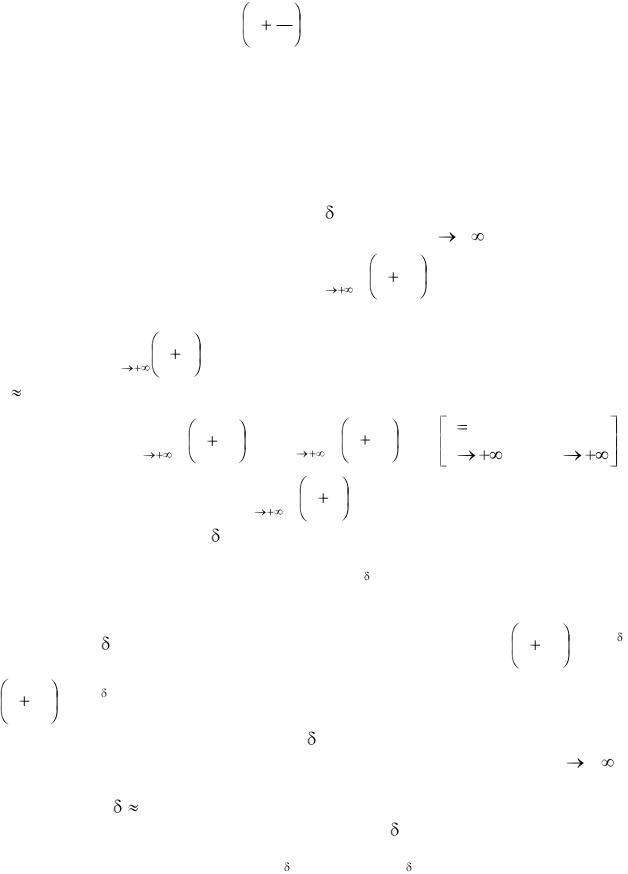
Непрерывные проценты наращения. Сила роста

j m n

Если в формуле S = P 1 , определяющей наращённую сумму при m

использовании номинальной процентной ставки наращения j, длительность периодов начисления процентов постоянно уменьшать, то количество m этих периодов в году будет увеличиваться. В пределе при стремлении длительности периодов к нулю их число стремится к бесконечности. Такое начисление процентов называется непрерывным, а процентная ставка при непрерывном начислении называется силой роста. Непрерывное наращение используется на практике при анализе характеристик ценных бумаг.

Из курса высшей математики известен так называемый второй замечательный

большом числе периодов начисления процентов m (несколько десятков, сотен и

Задача 5. На сумму 20 000 р. начисляются проценты по сложной годовой ставке i% = 12% в течение 4-х лет. Определить силу роста и наращённую сумму.

Решение. Здесь i=0.12, m=1. Тогда = ln(1 + 0.12) 0.1133. Тогда наращённая сумма, вычисленная через силу роста

S = 20 000e0.1133 4 31470 р. 39 коп.

Естественно, тот же самый результат получается при начислении сложных процентов в течение 4-х лет:

S = 20 000(1+0.12)4 31470 р. 39 коп.

Номинальная и эффективная учетные процентные ставки при дисконтировании

Если дисконтирование применяют m раз в году, используют номинальную учетную ставку f. Тогда в каждом периоде, равном 1/m части года, дисконтирование осуществляется по сложной учетной ставке f/m. Ранее рассматривалось дисконтирование в случае m=1, учетная ставка обозначалась d и имела место формула P = S(1– d)n, где n – количество единичных промежутков (лет). В общем случае процесс дисконтирования по сложной учетной ставке f/m

описывается формулой

P = S(1 – f/m)n m .

Под эффективной учетной ставкой понимают сложную годовую учетную ставку dсл, эквивалентную по финансовым результатам номинальной, применяемой

при m операций дисконтирования в году. Величина dсл находится из равенства

дисконтных множителей (1– dсл)n = (1 – f/m)n m . Имеем dсл = 1– (1 – f/m)m .

Задача 6. Вексель на сумму 20 000 р., срок платежа по которому наступает через 1.5 года, учтен по сложной процентной ставке 18% годовых. Найти эффективную учетную ставку dсл. Также определить сумму P, полученную владельцем векселя при учете.

Решение. Здесь f=0.18, m=4, n=1.5. Тогда

dсл = 1– (1 – 0.18/4)4 = 0.168210399375.

Указанную сумму можно вычислить двумя способами:

P=20 000(1– dсл)1.5 15 172 р. 26 коп., P=20 000(1– 0.18/4)1.5 4 15 172 р. 26 коп.