Лекция№8-тпр (1) 2.1014

Лекция №8.

Распределительная задача.

КТЗ обобщается в различных направлениях. Одним из наиболее часто встречающихся обобщений является так называемая распределительная задача. Далее будут рассмотрены некоторые практические задачи, приводящие к распределительной задаче или ее модификациям.

1. Распределение заказов по предприятиям.

Пусть имеется m видов заказов, причем заказ i-того вида необходимо выполнить в количестве единиц (). Эти заказы могут быть размещены на n предприятиях. Стоимость выполнения единицы i-того вида заказа на j-том предприятии равна . Для производства единицы продукции i-того вида на j-том предприятии расходуется некоторый ресурс в количестве (например, сырье, трудовые ресурсы и т.п.), причем для каждого предприятия ресурс ограничен величиной .

Необходимо распределить заказы по предприятиям так, чтобы выполнить все заказы имеющимися ресурсами предприятий и при этом суммарная стоимость выполнения заказов была бы минимальной.

Построение ММ.

Пусть - количество заказов вида i, выполняемых на j-том предприятии. Тогда ММ задачи будет иметь вид:

(1)

(2)

(3)

(4)

Здесь целевая функция (1) отображает суммарную стоимость выполнения заказов. Ограничения (2) требуют, чтобы расходуемые ресурсы на предприятиях не превышали заданной величины запасов. Ограничения (3) требуют выполнения всех заказов в необходимых объемах. Ограничения (4) очевидны. Задача (1) –(4) относится к классу ЗЛП . Она отличается от КТЗ (открытой) тем, что коэффициент .

К модели вида (1)-(4) сводится также известная задача о распределении самолетов по авиалиниям.

2. Распределение самолетов по авиалиниям.

Пусть имеются n типов самолетов, которые должны быть использованы для перевозки пассажиров по m авиалиниям. Число самолетов j-того типа равно . Исходя из данных о себестоимости пассажирокилометра и коммерческой загрузки каждого типа самолетов на каждой авиалинии, устанавливаются:

• месячные объемы перевозок пассажиров одним самолетом j-того типа по i-той линии.

• месячные затраты 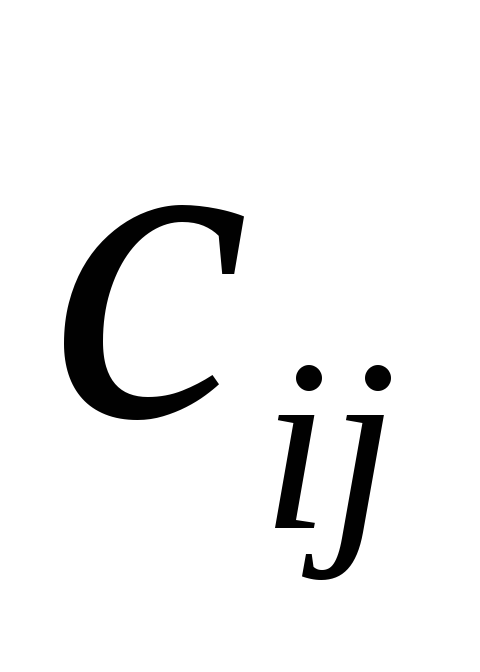на эксплуатацию одного самолета j-того вида на i-той линии.

Предполагается также известным число пассажиров , подлежащих перевозке в течение месяца по i-той линии.

Необходимо распределить самолеты по авиалиниям для перевозки заданного количества пассажиров при минимальных затратах.

Построение ММ.

Обозначим через число самолетов j-того типа на i-той авиалинии. Тогда ММ задачи запишется:

(1)

(2)

(3)

, целые (4)

По физическому смыслу параметры этой задачи, как и в предыдущей, должны быть целыми числами. В отличие от КТЗ в распределительной задаче целочисленность решения не гарантируется, если это условие не включено в систему ограничений. Нарушение условия целочисленности в задачах подобного рода , когда не равные нулю принимают, вообще говоря, немалые значения, приводит как правило к несущественным отклонениям от оптимума. При дробных в качестве компонент решения задачи следует принимать ближайшие к ним целые числа. Требование целочисленности оказывается существенным, если значения ограничены малыми числами.

3. Планирование парка вагонов.

Одно из важнейших условий экономичной эксплуатации железных дорог заключается в рациональном планировании использования парка вагонов не только в пределах дороги, но и в пределах станции или узла. Под регулированием парка вагонов понимают распределение вагонов различных типов (крытых, полувагонов, платформ с разным числом осей и т.д.) под различные грузы.

Пусть имеются n видов вагонов , в которые могут быть погружены грузы m видов . Количество вагонов j-того вида составляет штук. Норма загрузки вагона j-того вида грузом i-того вида составляет . Количество грузов i-того вида, которое необходимо погрузить, определяется величиной . Эксплуатационные расходы на погрузку i-того вида груза в один вагон j-того типа составляет . Требуется определить такое распределение вагонов, при котором все грузы были бы погружены в имеющиеся вагоны, а суммарная стоимость погрузки всех грузов была бы минимальной.

Построение ММ.

Пусть - число вагонов j-того типа, выделенных под погрузку грузом i-того вида. Тогда ММ задачи запишется:

(1)

(2)

(3)

, (4)

Целевая функция (1) отражает суммарную стоимость погрузки всех грузов, ограничение (2) требует, чтобы грузы каждого вида были погружены полностью, ограничение (3) требует, чтобы грузы были погружены в имеющееся количество вагонов.

К задаче вида (1)-(4) сводятся также задачи планирования работы речного флота. Так при анализе практических проблем Волжского речного пароходства к распределительной задаче сведены задачи распределения однородного грузового флота по грузовым линиям, пассажирского флота по линиям, задачи распределения по объектам перегрузочных машин, дноуглубительных снарядов и т.д.

Задачи дискретного программирования.

Многие задачи ИСО, такие, как распределение ресурсов, сетевого планирования и управления, календарного планирования, описываются математическими моделями ДП.

Рассмотрим задачу вида:

(1)

(2)

(3)

Здесь , G- некоторое множество n-мерного пространства . Если множество G является конечным или счетным, то условие (3) – это условие дискретности. В таком случае данная задача является задачей дискретного программирования (ЗДП).

Если вводится ограничение - целые числа, то приходят к задаче целочисленного программирования, которая является частным случаем ЗДП.

Если условие целочисленности накладывается только на часть компонент вектора Х, то задача (1)-(3) будет задачей частично-целочисленного программирования.

Если компоненты вектора Х могут принимать только 2 значения-0 или 1, то (1)-(3) – задача булевского программирования.

В задачах ДП область допустимых решений является невыпуклой и несвязной. Поэтому отыскание решения таких задач сопряжено со многими трудностями. В частности, практически невозможно применение стандартных приемов, используемых при замене дискретной задачи ее непрерывным аналогом, состоящих в дальнейшем округлении найденного решения до ближайшего целочисленного. Например, рассматривается ЗЦЛП:

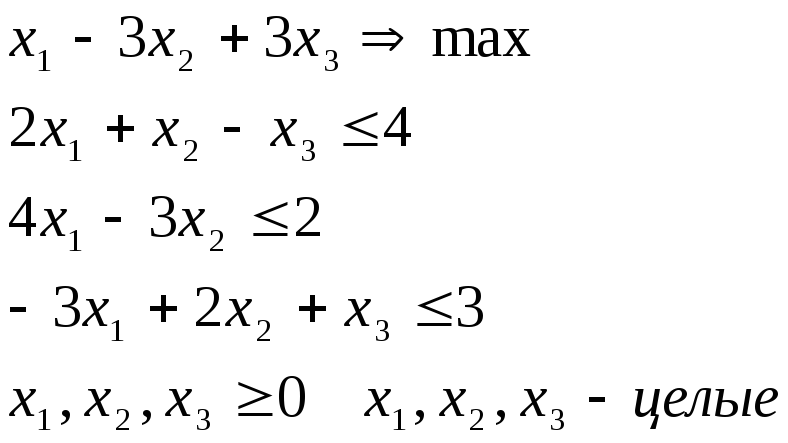
Решение соответствующей ЗЛП без требования целочисленности Х*=(0,5; 0; 4,5), а искомое целочисленное решение Х*=(2; 2; 5).

Если множество G конечно, то наиболее простой метод решения задачи (1)-(3) состоит в прямом переборе. Суть метода: в любом порядке перебираются множества возможных значений Х и для каждого значения вычисляется значение целевой функции f(Х). Далее находится наибольшее (наименьшее) значение f(Х*), которое будет соответствовать оптимальному решению Х*G. Однако в реальных задачах хотя G и конечно, но его размерность бывает очень большой, и такой перебор становится практически невозможным.

Поэтому для решения ЗДП разрабатываются специальные методы, основанные на принципе целенаправленного перебора, которые позволяют сократить полный перебор. Методы решения ЗДП по принципу подхода к проблеме делятся на 3 группы:

1. Методы отсечения, или отсекающих плоскостей

2. Метод ветвей и границ

3. Методы случайного поиска и эвристические методы