
PraktykumLA+AG
.pdf
|
|
|
|
|
|
|
|
Розділ 1. ЛІНІЙНА АЛГЕБРА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
Досліджують систему на сумісність |
Якщо хоча б один з вільних членів |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
(теорема Кронекера — Капеллі). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
i,i r 1,m, відмінний від нуля, то |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
система несумісна. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Якщо |
|
|
ж |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
0,i r 1,m, |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
система сумісна. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
разі |
сумісності, |
перетворюють |
|
|
... |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1 ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
східчасту |
матрицю |
до |
зведеного |
|
|
|
0 |
|
|
1 |
|
|
|
... |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||
|
0 ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
... |
|
|
|
|
|
|
... |
|
|
|
||||||||||||
|
східчастого вигляду. |
|
|
... ... ... ... |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
0 ... |
|
|
0 |
|
|
0 |
|
|
|
... |
|
0 |
|
|
|
|
1 |
|
|
... |
|
... |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
Знаходять розв’язки одержаної системи. Можливі 2 випадки: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1) кількість змінних дорівнює рангові |
|
|
|
|
x1 |
|
1, |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
матриці системи (n r); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
2, |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.......... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
r |
|
|
r |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2) кількість змінних n більше |
|
|
|
|
|
|
|
|
|
|
|
|
C ... |
C |
|
|
, |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1,r 1 1 |
|
|
|
|
|
|
1,n n r |
|
|
|
||||||||||||||
|
кількості рівнянь r |
(n r). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
... |
|
C |
|
|
|
, |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
2 |
2 |
|
|
|
|
|
|
|
r |
|
|||||||||||||||||||||||||
|
Змінні, які відповідають лідерам |
|
|
|
|
|
|
|
|
|
|
|
|
2,r 1 1 |
|
|
|
|
|
|
|
2,n n |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
* |
................................................ |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
рядків називають базисними |
, а решту |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
... |
|
C |
|
|
|
, |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
r |
r |
|
r |
|
|
|
|
|
r |
|
|||||||||||||||||||||||||
|
змінних — вільними. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,r 1 1 |
|
|
|
|
|
|
r,n n |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
, j 1,n r. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Надають вільним змінним довільних |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
r j |
|
|
|
|
|
|
j |
|
|
|
|
n r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
значень C |
,...,C |
|
і виражають через |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1,r j |
j |
|
|
|
|
|
|
|
|
|
|||||||||
|
них базисні змінні. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Нехай |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
y1,y2,...,yr |
— базисні змінні; |
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,r j |
j |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
,y |
|
,...,y — вільні змінні |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
r 1 |
r 2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* Кожне рівняння містить лише одну базисну змінну.

22 Розділ 1. ЛІНІЙНА АЛГЕБРА
1.17. Однорідні і неоднорідні СЛАР
Однорідні й неоднорідні СЛАР. |
Однорідна СЛАР завжди сумісна, бо в |
|||||||||||
СЛАР називають однорідною, якщо |
неї існує тривіальний розв’язок |
|||||||||||
вільні члени всіх рівнянь нульові, і |
|
|
|
|
|
|
|
|
|
|
||
x 0. Будь-яка лінійна комбінація |
||||||||||||
неоднорідною, якщо хоч один з них |
розв’язків однорідної СЛАР є |
|
|
|||||||||
відмінний від нуля. |
розв’язком цієї системи. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Дослідження однорідної СЛАР. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rang A r |
|
|
|
|
||||
Якщо ранг матриці Am n однорідної |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СЛАР дорівнює r, то система має |
|
|
|
СЛАР Ax |
|
0 |
|
|
|
|||
n r лінійно незалежних розв’язків |
|
|
|
r n |
r n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e1,e2,...,en r , які утворюють |
|
|
|
|
|
|
|
|
|
|
|
|
|
безліч розв'язків |
|
|
єдиний розв'язок |
|
|||||||
фундаментальну систему розв’язків |
|
|
|
|
|
|
|
|||||
|
з (n r) сталими |
|
|
|
x |
0 |
|
|||||
(ФСР). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кожний розв’язок однорідної СЛАР |
|
|
|
|
|
|
|
|
|
|
|
|
лінійно виражається через сукупність |
|
|
|
|
|
|
|
|
|
|
|
|
розв’язків, які утворюють ФСР цієї |
|
|
|
|
|
|
|
|
|
|
|
|
системи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Структура загального розв’язку |
|
|
|
|
|
|
|
|
|
|
|
|
однорідної СЛАР. Якщо {e1,...,en r } |
|
|
|
xзаг. одн. |
|
|||||||
— ФСР однорідної СЛАР, то |
|
|
|
|
|
|
|
|||||
загальний розв’язок системи є |
|
C1e1 C2e2 |
... Cn ren r |
|||||||||
лінійною комбінацією розв’язків |
|
|
|
|
|
|
|
|
|
|
|
|
e1,...,en r . |
|
|
|
|
|
|
|
|
|
|
|
|
Структура загального розв’язку |
|
|
|
|
|
|
|
|
|
|
|
|
неоднорідної СЛАР. Загальний |
|
|
|
|
|
|
|
|
|
|
|
|
розв’язок неоднорідної СЛАР |
|
xзаг. неодн. |
|
xзаг. одн. xчаст. неодн. |
||||||||
дорівнює сумі загального розв’язку |
|
|
||||||||||
відповідної однорідної СЛАР* і |
|
|
|
|
|
|
|
|
|
|
|
|
деякого частинного розв’язку |
|
|
|
|
|
|
|
|
|
|
|
|
неоднорідної СЛАР. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Однорідна СЛАР із квадратною матрицею A
|
detA 0 |
система має єдиний |
Однорідна СЛАР має ненульовий |
||
|
|
|
|
|
розв’язок тоді й лише тоді, коли |
|
розв’язок x 0; |
||||
|
detA 0 |
система має безліч |
detA 0. |
||
|
|
||||
|
розв’язків |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
||
|
|
Неоднорідній СЛАРAx b відповідає однорідна СЛАР Ax 0. |
|||
Розділ 1. ЛІНІЙНА АЛГЕБРА |
23 |
1.18. Розв’язання матричних рівнянь
Метод оберненої матриці |
A |
X |
n l |
B |
n l |
X A 1B; |
|
n n |
|
|
|
||
(для невироджених матриць A) |
Xm nAn n Bm n X BA 1 |
|||||
|
|
|
|
|||
Метод Ґауса — Йордана |
An nXn l |
Bn l : |
|
|||
(для невироджених матриць A) |
|
|
елементарні перетворення |
|||
(A | B) |
||||||
|
|
|
рядків розширеної матриці |
|||
|
(En | X) |
|
|
|
|
|
|
|
|
|
|
|
|

Розділ 2. ВЕКТОРНА АЛГЕБРА
2.1. Вектори
|
Геометричний вектор. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Геометричним вектором називають |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
||||||||||||||||
|
напрямлений відрізок. Першу точку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
напрямленого відрізка називають |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||||||||||||||||||||||
|
початком вектора, а другу — кінцем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектора. Довжиною вектора |
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
називають довжину відрізка AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
і позначають як |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Колінеарність векторів. Вектори |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
називають колінеарними (позначають |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
), якщо вони лежать на одній прямій |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|||||||||||||||||||||
|
або на паралельних прямих. |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
b |
|||||||||||||||||||||||||||||
|
|
|
|
|
a |
(a |
|||||||||||||||||||||||||||||||||||||||
|
Колінеарні вектори можуть бути: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
||||||||||||||||||||||||||
|
1) однаково-напрямлені (позначають ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2) протилежно напрямлені |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
b |
) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
a |
|||||||||||||||||||||||||||||||||||||
|
(позначають ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Компланарність векторів. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
a |
||||||||||||||||||||||||||||||||||||||||||||
|
Вектори називають компланарними, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
якщо вони лежать в одній або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
паралельних площинах . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
||||||||||||||||||
|
P |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Нульовий вектор. Якщо початок і |
Одиничний вектор. Вектор, |
|||||||||||||||||||||||||||||||||||||||||||
|
кінець вектора збігаються, то вектор |
довжина якого дорівнює одиниці, |
|||||||||||||||||||||||||||||||||||||||||||
|
називають нульовим і позначають |
|
|
називають одиничним. |
|||||||||||||||||||||||||||||||||||||||||
0. |
|||||||||||||||||||||||||||||||||||||||||||||
|
Нульовий вектор вважають |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
колінеарним будь-якому векторові. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Протилежні вектори. Вектори, які |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||||||||||||||||||||||||||
мають однакову довжину і протилежно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|||||||||||||||||||||||||
напрямлені, називають протилежними. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Колінеарність розглядають для двох і більше векторів.
Компланарність розглядають для трьох і більше векторів.

|
|
Розділ 2. ВЕКТОРНА АЛГЕБРА |
|
25 |
|||||
2.2. Дії над векторами |
|
|
|
|
|
|
|||
Рівність векторів. Два вектори |
|
a |
|
|
|||||
називають рівними, якщо вони |
|
|
b |
|
|||||
|
|
|
|
||||||
колінеарні, однаково напрямлені і |
|
|
|
|
|||||
мають ту саму довжину. |
|
|
|
a b |
|
|
|||
Відкладання вектора від точки. |
|
|
B |
|
|||||
Від будь-якої точки можна відкласти |
|
a |
|
||||||
|
|
|
|||||||
вектор, рівний заданому. |
|
|
|
A |
a AB |
|
|||
|
|
|
|
|
|
|
|
||
Додавання (віднімання) векторів |
|
|
|
|
|||||
правило |
правило |
|
правило замикача |
різниця векторів |
|||||
трикутника |
паралелограма |
||||||||
|
|
|
|
||||||
|
A |
|
|
B |
A2 |
|
A |
|
|
|
|
|
a2 |
|
|
|
|||
a |
b |
A |
|
|
A1 |
an |
a |
C |
|
|
|
a1 |
An |
|
|||||
|
|
a |
|
|
b |
|
|||
|
|
|
C |
O a1 a2 |
|
||||
O |
|
|
... an |
O |
|
||||
a b |
B |
b |
|
|
|
|
|
||
|
|
O |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Множення вектора на число |
|
1 |
|
2a |
|
||||
a — вектор: |
|
|
|
2 a |
|
|
|||
|
|
|
|
|
|
|
|||
1) a |
a ; |
|
|
|
a |
|
|
||
a a, якщо 0, |
|
|
|
|
|
|
|||
2) a a, якщо 0 |
|
|
|
|
|
|
|||
Властивості лінійних дій над векторами |
|
|
|
||||||
a b b a; |
|
|
1 a a, ( a ) ( 1) a; |
|
|||||
(a b ) c a (b c ); |
|
|
( a ) ( ) a; |
|
|||||
0 a a; |
|
|
|
(a b ) a b ; |
|
||||
a ( a ) 0 |
|
|
( ) a a a |
|
|||||
Орт. Ортом вектора a називають |
|
a 0 |
1 a |
|
|||||
одиничний вектор a 0, який однаково |
|
|
|||||||
|
|
a |
|
||||||
напрямлений з вектором a. |
|
|
|
a a a 0 |
|
||||
|
|
|
|
|
|
|
|||

26 |
Розділ 2. ВЕКТОРНА АЛГЕБРА |
2.3. Лінійна залежність (незалежність) векторів
Лінійна комбінація векторів. Лінійною комбінацією векторів a1,a2,...,an з
коефіцієнтами |
, |
,..., |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
. |
||||||||||||||
|
|
|
|
називають вектор b |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
n |
a |
a |
2 |
a |
||||||||||||||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
1 1 |
2 |
|
|
|
|
|
n n |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Лінійна незалежність (залежність) системи векторів |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Система векторів |
|
|
|
|
|
|
|
|
|
лінійно Система векторів |
|
|
|
|
|
|
|
|
|
|
лінійно |
|||||||||||||||||||
a1,a2,...,an |
a1,a2,...,an |
|||||||||||||||||||||||||||||||||||||||
незалежна, якщо з рівності |
|
|
|
|
залежна, якщо існують такі числа |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, 2,..., n, не рівні одночасно |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1a1 2a2 ... nan |
|
0 |
||||||||||||||||||||||||||||||||||||||
нулеві, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
випливає, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1a1 2a2 ... nan |
0. |
|||||||||||||||||||||||||||
1 2 ... n |
0. |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Геометричний зміст лінійної залежності (незалежності) векторів
Один вектор лінійно залежний (незалежний) тоді й лише тоді, коли він нульовий (ненульовий).
Система із двох векторів лінійно залежна (незалежна) тоді й лише тоді, коли вектори колінеарні (неколінеарні).
Система із трьох векторів лінійно залежна (незалежна) тоді й лише тоді, коли вони компланарні (некомпланарні).
На прямій, на площині й у просторі існують лінійно незалежні системи відповідно з одного, двох та трьох векторів.
На прямій, на площині й у просторі будь-які системи відповідно із двох, трьох та чотирьох (і більше) векторів лінійно залежні.
2.4. Базис
|
Векторний геометричний |
Базис і вимірність векторного |
|||||||||||||||||
|
простір. Множину геометричних |
простору. Базисом векторного |
|||||||||||||||||
|
векторів з означеними лінійними діями |
простору називають будь-яку |
|||||||||||||||||
|
над векторами називають векторним |
лінійно незалежну систему з |
|||||||||||||||||
|
(геометричним) простором. |
найбільшою можливою кількістю |
|||||||||||||||||
|
|
|
|
|
|
|
|
векторів. Кількість векторів базису |
|||||||||||
|
|
|
|
|
|
|
|
простору називають його вимірністю. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Базис на прямій утворює будь-який |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
OM |
|
|||||||||
|
ненульовий вектор |
|
. Будь-який |
|
|
|
|
|
|
|
a |
|
|||||||
|
|
|
e |
|
|
|
|
||||||||||||
e |
|
|
|||||||||||||||||
|
вектор a |
прямої єдиним чином |
O |
|
|
E |
|
|
|
|
M |
1 |
|||||||
лінійно виражається через вектор |
|
. |
|
|
|
|
|
|
|
|
|||||||||
e |
|
|
|
|
ae |
||||||||||||||
|
|
|
|
a |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вектор b лінійно виражається через вектори a1,a2,...,an.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розділ 2. ВЕКТОРНА АЛГЕБРА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Базис на площині утворює будь-яка |
|
|
|
|
|
|
|
|
E2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
впорядкована пара неколінеарних |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
векторів |
|
|
та |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
e1 |
e2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Будь-який вектор площини єдиним |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
чином лінійно виражається через |
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
e1 E M |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
вектори базису { |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
||||||||||||||||||||
|
e1,e2}. |
|
|
|
|
|
|
a1 |
e1 a2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
e2 |
|
|
|
|
|||||||||||||||||||
|
Базис у просторі утворює будь-яка |
|
|
|
|
|
|
|
|
|
|
|
M3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
впорядкована трійка некомпланарних |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
векторів |
|
, |
|
|
та |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E3 |
|
|
|
|
|
|
|
|
||||||||||||
|
e |
e |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
||||||||
|
Будь-який вектор простору єдиним |
|
|
|
|
|
|
e3 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||
|
|
e1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
чином лінійно виражається через |
|
|
|
|
|
|
|
|
|
e2 |
M2 E2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
вектори базису {e1,e2,e3}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
e1 a2 |
e2 a3 |
e3 |
|
|
||||||||||||||||||||||||
2.5. Координати вектора
Розкладення вектора за базисом. |
Вибраний базис встановлює |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Співвідношення |
взаємно однозначну відповідність між |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x1 |
e1 x2 |
e2 x3 |
|
|
|
|
|
|
векторами і їхніми координатними |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
e3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
називають розкладом вектора |
|
|
|
|
стовпцями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
за базисом {e1,e2,e3}. Числа x1, x2, x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
||||||||
називають координатами вектора x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
x x{e |
,e |
,e |
} |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
у базисі {e ,e ,e }. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1 2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
{ |
e |
, |
e |
, |
e |
} |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
3 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де x{ |
|
, |
|
|
|
, |
|
|
} |
— координатний стовпець |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
e |
e |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектора |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Рівність векторів. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рівним векторам відповідають рівні |
x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||
координати. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
{ |
|
, |
|
, |
|
|
} |
|
|
|
|
|
|
3 |
{ |
|
, |
|
, |
|
} |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
e |
e |
|
|
|
|
|
e |
e |
e |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Додавання (віднімання) векторів. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Додаванню (відніманню) векторів |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
відповідає додавання (віднімання) їх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
{ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1,e2,e3 } |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
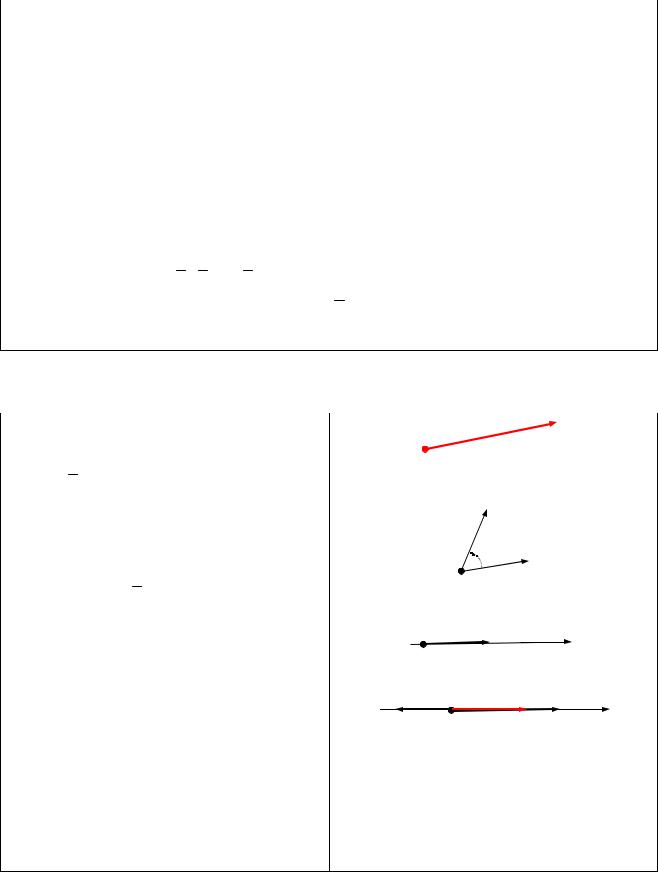
|
28 |
|
|
|
|
|
|
|
Розділ 2. ВЕКТОРНА АЛГЕБРА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Множення вектора на число. |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Множенню вектора на число |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
відповідає множення всіх його |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
координат на це число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
{ |
|
, |
|
, |
|
} |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
e |
e |
e |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Умова колінеарності векторів. |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Вектори x 0 та y |
колінеарні тоді й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
y y2 |
|
|
|||||||||||||||||||||
|
лише тоді, коли існує таке число , що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
||||||||
|
y x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Координати колінеарних векторів у |
|
|
|
x1 |
|
|
x2 |
|
|
x3 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
фіксованому базисі пропорційні. |
|
|
|
|
|
|
y1 |
|
|
|
y2 |
|
|
y3 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система векторів a1,a2,...,an лінійно незалежна тоді й лише тоді, коли система їхніх координатних стовпців a1,a2,...,an у вибраному базисі лінійно незалежна.
2.6. Декартова система координат
Радіус-вектор. Радіусом-вектором |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
rM |
M |
|||||||||||||||||||||
точки M (щодо точки O) називають |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
O |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектор |
rM OM . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Кут між векторами. Кутом між |
|
|
|
|
|
A |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
векторами |
|
|
OA та b OB |
|
|
|
|
|
|
|
|
||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
вважають величину кута AOB і |
|
|
|
|
|
|
|
|
|
|
|
B |
|||||||||||||||
позначають ( |
|
|
|
|
O |
|
|
|
|
b |
|||||||||||||||||
|
|
||||||||||||||||||||||||||
|
,b ). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Система координат на прямій. |
O |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
i |
|
|
|
|
|
|
x |
||||||||||||||||||||
Сукупність {O; |
|
} точки O (початку |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
координат) і базису з одиничного |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
вектора |
|
називають декартовою |
M2 |
O |
|
|
|
|
|
|
M1 |
||||||||||||||||
|
i |
||||||||||||||||||||||||||
i |
|||||||||||||||||||||||||||
системою координат на прямій. |
x2 0 |
0 |
|
|
|
|
|
|
|
|
1 x1 0 x |
||||||||||||||||
Пряму, на якій запроваджено систему
координат, називають координатною віссю Ox.

Розділ 2. ВЕКТОРНА АЛГЕБРА |
|
|
|
|
|
|
29 |
|||||
ПДСК на площині. Сукупність |
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
My |
|
|
M(x;y) |
|
|||
{O; i , j } точки O (початку координат) |
|
|
|
|
|
yj |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
і базису з одиничних |
j |
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
rM xi yj |
|
|||||
перпендикулярних векторів i та j |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
називають прямокутною декартовою |
O |
|
i |
|
x |
|
|
xi |
|
i |
|
|
системою координат (ПДСК) на |
|
вісь абсцис |
O |
|
Mx |
|
x |
|
||||
площині. |
|
|
|
|
|
|
|
|
|
|
|
|
Осі координат: |
|
|
|
|
|
|
|
|
|
|
|
|
1) вісь абсцис Ox i ; |
|
|
|
|
|
|
|
|
|
|
|
|
2) вісь ординат Oy j . |
|
|
|
|
|
x — абсциса; |
|
|
||||
|
r |
|
x |
|
|
|
|
|
|
|
|
|
Площину, на якій запроваджено |
|
|
|
y — ордината. |
|
|||||||
M |
|
|
|
|
|
|||||||
|
|
|
y |
|
|
|
|
|
|
|
||
систему координат, називають |
|
|
|
|
{i ,j } |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координатною площиною Oxy. |
|
|
|
|
|
|
|
|
|
|
|
|
Координати точки M(x;y) — це |
|
|
|
|
|
|
|
|
|
|
|
|
координати її радіуса-вектора |
|
|
|
|
|
|
|
|
|
|
|
|
ПДСК у просторі. Сукупність |
|
|
|
|
z |
|
|
|
|
|
|
|
{O;i , j ,k } точки O (початку |
|
|
Mz |
|
|
|
|
|
|
|
||
|
|
|
|
|
M |
|
|
|
|
|
|
|
координат) і базису з одиничних |
|
|
|
|
zk |
|
|
|
|
|
|
|
попарно перпендикулярних векторів |
|
|
|
|
|
|
|
|
|
|
|
|
i , j та k називають прямокутною |
|
|
|
|
k |
rM xi |
yj |
zk |
|
|||
декартовою системою координат |
|
|
|
|
|
|
||||||
|
|
|
|
|
j |
yj |
|
|
|
|
|
|
(ПДСК) у просторі. |
|
|
|
|
O |
My |
|
y |
|
|
||
Осі координат: |
Mx |
|
|
|
|
|
|
|
|
|||
xi |
|
|
|
|
|
|
|
|||||
1) вісь абсцис Ox i ; |
|
|
|
|
|
|
|
|
|
|||
x |
i |
|
|
|
|
|
|
|
|
|
|
|
2) вісь ординат Oy j ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) вісь аплікат Oz k . |
|
|
|
|
|
|
|
|
|
|
|
|
Координатні площини: Oxy,Oyz,Oxz. |
|
|
|
|
x — абсциса; |
|
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
Координати точки M(x;y;z) — це |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
y — ордината; |
|
|||||||
|
y |
|
|
|||||||||
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
координати її радіуса-вектора |
|
|
|
|
z — апліката |
|
|
|||||
|
|
z |
|
|
|
|||||||
|
|
|
|
{i ,j ,k } |
|
|
|
|
|
|
|
|
Координати вектора з початком |
|
|
|
|
A |
|
|
|
|
xA |
|
|
|
|
|
|
|
|
|
xB |
|
||||
|
|
rA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A(xA;yA;zA) і кінцем B(xB ;yB ;zB ) |
|
|
|
|
|
|
|
|
|
yA |
|
|
|
|
|
|
|
AB yB |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
rB |
|
|
|
|
|
z |
|
|
|
|
|
B |
|
|
z |
B |
A |
|
||||
AB rB rA. |
|
|
|
|
|
|
|
|
|
|||
|
y |
|
|
|
|
|
|
|
|
|
|
|
O x |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||

30 |
|
Розділ 2. ВЕКТОРНА АЛГЕБРА |
|
|
|
|
|
|
|
|
|
|
|||
Координати точки поділу відрізка |
A |
z |
M |
B |
x |
|
x |
A |
x |
B |
; |
||||
AB з кінцями |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
||||||||
A(xA;yA;zA),B(xB ;yB ;zB ). |
|
|
y |
|
|
|
|
|
|
|
|
||||
O |
x |
|
|
|
y y |
B |
|
||||||||
|
|
|
|
|
|
y |
|
|
|
A |
|
; |
|||
Кажуть, що точка M поділяє відрізок |
|
|
|
|
|
|
|
1 |
|
||||||
AB у відношенні 1, якщо |
|
|
|
|
z |
zA |
zB |
, |
|||||||
виконано співвідношення |
|
|
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
AM MB. |
|
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Координати середини відрізка AB |
|
x xA xB , y yA yB , |
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
z zA zB |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2.7. Проекція вектора на вісь |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Векторна проекція. Пряму L, на |
|
s |
|
|
|
|
B |
|
|
|
|
|
|||
якій вибрано додатний напрям |
|
|
|
L |
|
a |
|
|
|
|
|
L |
|||
(орієнтацію), називають віссю. |
Додатний напрям |
A |
|
|
|
|
|
B |
|||||||
Векторною проекцією вектора |
|
|
|
|
|
|
|
||||||||
осі позначають |
|
|
|
|
|
aL s |
|
|
|||||||
a AB на вісь L s |
називають |
стрілкою. |
|
|
|
A |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
вектор aL |
A B . |
|
Вектор s — напрямний вектор осі. |
|
|
||||||||||
Скалярна проекція. Проекцією |
таке, що |
|
|
|
|
|
|
|
|
|
|
||||
вектора a AB на вісь L з |
|
|
A B s 0,s 0 |
|
s . |
|
|
||||||||
напрямним вектором s |
називають |
|
|
|
|
||||||||||
число |
|
|
|
|
|
|
|
|
|
s |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
prL a prs a, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обчислення проекції вектора на |
prL a a |
|
|
|
|
|
|
|
|
|
|||||
вісь. Проекція вектора a на вісь L(s ) |
cos(a,L) a |
|
cos(a,s ) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дорівнює добутку довжини вектора a на |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
косинус кута між вектором a та віссю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Властивості проекції вектора на напрям |
|
|
|
|
|
|
|
|
|
|
|
||||
a b pr a pr b ; |
prs |
a 0, |
якщо s |
|
|
|
|
|
|
|
|
||||
|
L |
L |
|
|
|
|
|
|
|||||||
|
A B |
|
|
|
|
||||||||||
prL(a b ) prL a prL b ; |
prs |
a 0, якщо s |
a |
|
|
|
|
|
|
|
|||||
pr ( a) pr a |
|
prs |
a 0, |
якщо s |
|
|
|
|
|
|
|
|
|||
L |
L |
|
A B |
|
|
|
|
||||||||
