Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

MetodMechanics (1)

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

957.22 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

значення до значення ω2. Яку середню потужність розвивають сили, що діють на циліндр?

Відповідь: =

( − )/4 .

№ 4.11. Однорідна куля масою = 5,0 кг зкочується без ковзання по похилій площині, яка утворює кут = 30 з горизонтом. Знайти кінетичну енергію кулі через = 1,6 с після початку руху.

Відповідь:

sin = 0,11

кДж.

№ 4.12.

Дзиґа=

до

масою

= 0,50

кг, вісь якої похилена під кутом

= 30

вертикалі, процесіює під2

дією сили тяжіння. Момент інерції дзиґи відносно її

осі симетрії

= 2,0

г·м , кутова швидкість обертання навколо цієї осі

рад/с,

= 10

відстань від точки опори до центру мас дзиґи

см. Знайти:

350а) кутову швидкість прецесії дзиґи;

б) модуль та напрям горизонтальної складової сили реакції, що діє на дзиґу в точці опори.

Відповідь: a)		= g /	= 0,7	рад/с,
б)					мН. Ця сила напрямлена в сторону,
протилежну		=	sin = 10
	нахилу дзиґи.

5. Гармонічні коливання. Осцилятор

Рівняння гармонічних коливань і його розв’язок:

x + ω02x = 0, x = Acos(ω0t + α ),

де ω0 − власна частота коливань

Рівняння згасаючих коливань і його розв’язок:

x + 2β x + ω02x = 0, x = A0e−β t cos(ωt + α ),

де β − коефіцієнт згасання, ω − частота згасаючих коливань:

ω =	ω02 − β 2
Логарифмічний декремент згасання λ та добротність Q :
λ = βT ,	Q = π λ ,

де T = 2π ω − період згасаючих коливань.

Рівняння вимушених коливань і його усталений розв’язок:

− ϕ ),

де

+ 2β x + ω0 x = f0 cosωt, x = Acos(ωt

2βω

A =

tgϕ =

f0 =

ω02 − ω 2

− ω

)

2 2

(ω0

+ 4β ω

* * *

Приклад 5.1.

Обчислити період малих коливань ареометра (див. рис.), якому надали невеликого поштовху в вертикальному напрямі. Маса ареометра m = 50г, радіус його трубки

r = 3,2мм, густина рідини ρ = 1,00г/см3 . Опір рідини нехтовно малий.

Розв’язання.

До поштовху була рівновага, тобто

mg = ρ gπ r2 h ,

де h − початкова глибина занурення ареометра.

Після занурення на невеличку глибину x на ареометр діяла сила вгору:

F = ρ gπ r2 (h + x).

Різниця

F − mg = ρ gπ r2 x .

F − mg дорівнює виштовхувальній (додатковій) силі −mx. Отже,

	+ ρ gπ r		2	x =0					+	ρ gπ r2	x =0 ,
										m
x								x		m
звідки								2π 2
		ρ gπ r2				2		2π 2
					=ω 0		=
		m			=ω 0		=	T
		m						T

T = ρ4πgrm2 = 2,5c.

При клад 5.2.

Однор дний стрижень поклали на два блоки, які ш видко обертаються, як показано на рисун у. Відстань між осями блока l =20см. Коефіцієнт тертя

між стрижнем і блоками k = 0,18. Показати, що стрижень буде виконувати гар монічні коливання. Знайти їх період.

Розв’язання.	(1)
+ = g.

Для моментів с л відносно осі O маємо:

	=					(2)
З (2) о римуємо	=		.
Підставляємо це в (1):						+

а оскільки l1 +l2 =l , то g =	1+	=					,

звідки	g =			,

Анало ічно,	=	g			.	(3)

6 2

(4)

Для сил тертя маємо:

ТР

=	=	g	,	(5)

=	=	g	.	(6)

Сили тертя напрямлені протилежно одна одній. Тому сумарна сила

тертя

ТР −

ТР

( − ).

(7)

Але (див. рисунок)

= ⁄2 + ,

= ⁄2 −

, тому

−

= 2 . Отже, (7) переходить в

2 .

Отже,

2 g

= 1,5 .

Приклад 5.3.

Є потік частинок маси

m , які рухаються з однаковою швидкістю υ

паралельно деякій осі OO′ . За площиною P,

перпендикулярною до цієї осі:

F = −xr , x − відома стала. Знайти найменшу відстань l від площини P до точки на осі OO′ , яку будуть перетинати всі частинки.

Розв’язання.

Сила F = −xr – гармонічна сила. Період коливань проекції зміщення будь-якої частинки на площину P є

T = 2π	m .
	x

Найменший час, потрібний для зустрічі частинки з віссю OO′ дорівнює

чверті періоду, тобто	π	m	. За цей час частинка пройде відстань уздовж
осі OO′ :	2	x
осі OO′ :
			l = υ	π	m
				2	x

Приклад 5.4.

Невеличкий брусок починає ковзати по похилій площині, що утворює кут α з горизонтом. Коефіцієнт тертя залежить від пройденого шляху s за законом k =as , де a − стала. Знайти час руху бруска до зупинки.

Розв’язання.

На брусок діють дві сили: 1) скочуюча mg sinα , 2) тертя kmg cosα або, за умовою задачі, asmg cosα .

Рівняння руху бруска в лабораторній (інерціальній) системі відліку:	( )
mω = mg sinα − asmg cosα	1
Коли б не було тертя, то брусок скачувався б з прискоренням
ω0 = g sinα .
Тепер перепишемо (1) так:
mω = mω0 − asmg cosα ,
або	(2)
m(ω − ω0 ) = −asmg cosα .	(2)

Очевидно, що ω − ω0 = ωвідн − прискорення бруска в системі відліку,

яка рухалась разом з бруском у відсутності сили тертя. В цій системі єдиною силою залишається тепер сила тертя. А оскільки вона пропорціональна −s , то в такій системі брусок буде гармонічно коливатися з частотою

ωвідн =	ag cosα ,
або з періодом	2π

T =		.
	ag cosα

Час від початку руху до зупинки дорівнюватиме найменшому проміжкові часу між двома станами спокою, тобто половині періоду:

	π
t =		.
	ag cosα

Приклад 5.5.

Уявімо собі шахту, що пронизує Землю вздовж її осі обертання. Вважаючи Землю однорідною кулею та нехтуючи опором повітря, знайти:

а) рівняння руху тіла, що впало в шахту; б) час, потрібний для того, щоб тіло досягло протилежного кінця шахти; в) швидкість тіла в центрі Землі.

	Розв’язання.
а)	Нехай x − координата тіла відносно центра Землі, m − маса тіла,
R − радіус Землі. На тіло діє сила з боку тієї частини Землі (кулі), радіус
якої дорівнює x . Маса цієї кулі M (x) = ρ										4 π x3 , де ρ − густина Землі.
				M з						3
Якщо M з − маса Землі, то ρ =				M з						, а тому
Якщо M з − маса Землі, то ρ =			(4 3)π R3							, а тому
			(4 3)π R3
	M (x) = M						x3	.		1
	M (x) = M							.		1
					з Rз3					( )
За другим законом Ньютона,					з Rз3
За другим законом Ньютона,				γ M (x)m
				γ M (x)m					,	(2),

	mx = −			x		2
де знак мінус означає, що сила		γ M (x)m напрямлена до центру Землі.
				x3

Узявши до уваги (1), останнє рівняння перепишемо так:

x + γ M3зx = 0 .

Rз

Оскільки нормальне прискорення вільного падіння

g = γ M з , Rз2

то рівняння руху тіла набере вигляду


			g			(3)
			R x = 0.
		x +
				з
б)	Одержано диференційне		рівняння гармонічного			коливання,
частота коливань якого ω0 =		g Rз , а період				(4)
	T = 2π Rз g .
Тому час проходження між двома крайніми точками шахти буде
	t = T	=π		Rз	= 42 хв.

	2			g

в) Запишемо для тіла рівняння гармонійного коливання в звичайній формі:

x = Rcos 2Tπ t

(амплітуда зміщення дорівнює радіусу Землі Rз ). Величину швидкості знайдемо, взявши похідну:

υ = −				2π R	sin 2π t .
				T
					T
Оскільки час руху тіла до центра дорівнює T 4 , то з останньої рівності
дістанемо			2π Rз			2π T
υ =	x	=

					sin
				T		T 4
і, згідно з (4),

υ = gRз = 7,9км/год.
Приклад 5.6.
Однорідний стержень маси m і завдовжки l							здійснює малі коливання

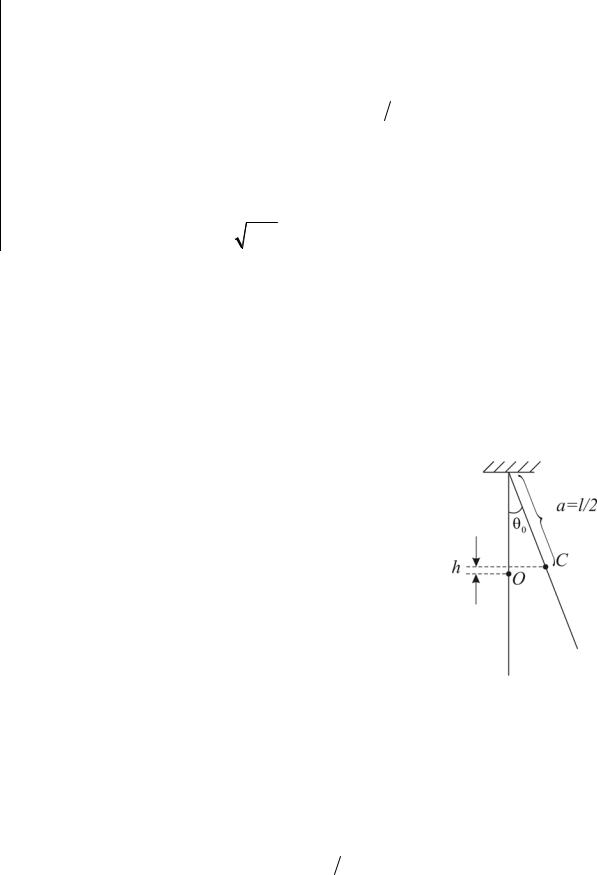
навколо горизонтальної осі, що проходить через його верхній кінець. Знайти середню за період коливання кінетичну енергію стержня, якщо в початковий

момент його відхилили від вертикалі на кут θ0								і надали йому		кутову
швидкість θ 0 .
		Розв’язання.
	Оскільки з умовою коливання малі, то вони є
	Оскільки з умовою коливання малі, то вони є
	гармонічними. А для гармонічних коливань середня
	за період кінетична (як і потенціальна) енергія
	дорівнює половині повній енергії коливання. Повна
	енергія складається з потенціальної в момент
	початкового відхилення та кінетичної, наданої
	стержневі	в цей момент. Потенціальна			енергія
	En = mgh ,	де h − висота підйому		центра				мас
	маятника (стержня) над точкою рівноваги				O (див.
	рис.).
	З рисунка видно, що					θ
		h = a(1 − cosθ0 ) = 2asin				θ
		h = a(1 − cosθ0 ) = 2asin			2		0	,
						2
	а оскільки коливання за умовою малі, то (при малих кутах відхилення)
	можна синус змінити даним кутом. Так що
		h = 2a	θ 2	aθ 2
		h = 2a	0 =	0 .
			4	2					mglθ 2
	Оскільки стержень однорідний, то a = l 2 , тому							E = mgh =	mglθ 2
	Оскільки стержень однорідний, то a = l 2 , тому							E = mgh =		0 .
								n	4
									4

Iθ 2

Початкова кінетична енергія Ek = 20 . Момент інерції стержня

відносно його кінця			I =		1	ml		2	, тому кінетична енергія E	=	1	2	2		, а
відносно його кінця			I =			ml			, тому кінетична енергія E	=		ml θ		0	, а
					3				k		6			0
	mglθ02				3						6
повна – E =	mglθ02	+	1		2		2
повна – E =	4	+	6	ml θ0 .
	4		6

Середня ж кінетична енергія за період коливання:

	mglθ02		1	2		2
E =		+		ml θ	0		.
k	8		12		0
	8		12

Приклад 5.7.

Два кубики з масами m1 і m2 з’єднали невагомою пружиною з

жорсткістю x і покласти на гладеньку горизонтальну площину. Потім кубики трохи зблизили і одночасно відпустили. Знайти власну частоту системи.

Розв’язання.

За третім законом Ньютона:

(1)

F2 = − F1

За другим законом Ньютона:

(2)

F1 = m1r1,

F2 = m2r1,

Згідно з (1),

Далі,

m2r2

= −m1r1 .

r2 − r1 = r

(див. рисунок)

− r1 = r , або (згідно з (2) і (1))

r = r2 − r1 =

−

= F2

Але F2 = − xr , тому

= − xr m

+ m

Позначимо

1	1
	+		.
m		m
2	1

(3)

μ називається зведеною масою двох взаємодіючих частинок. Тепер (3) запишемо у вигляді:

		x	(4)
	+	μ r = 0.
r

Остання формула є рівнянням гармонічного осцилятора. З (4) видно, що

x	= ω 2	або	ω	0	=	x	.

μ	0					μ

Приклад 5.8.

Точка здійснює згасаючі гармонічні коливання з частотою ω = 25c-1 . Знайти коефіцієнт згасання β , якщо в початковий момент швидкість точки дорівнює нулю, а її зміщення з положення рівноваги в η = 1,020 рази менше від амплітуди?

Розв’язання.

Запишемо рівняння згасаючого коливання: x(t) = A0e−β t cos(ωt + α ).

За початковою умовою,

x(0) = A0 η = A0 cosα .

Диференціюємо (1) по t . Дістаємо швидкість частинки: v(t) = −β x(t) − ω A0e− β t sin(ωt + α ).

За умовою v(0) = 0 , отже з (3) виходить:

0 = −β x(0) − ω A0 sinα ,

звідки, оскільки β > 0 ,

β = ω A0 sinα x(0)

або, враховуючи (2),

β = ω η 2 − 1 = 5c-1 .

(1)

(2)

(3)

Приклад 5.9.

Математичний маятник здійснює коливання в середовищі, для якого логарифмічний декремент згасання λ0 = 1,50. Яким буде значення λ , якщо

опір середовища збільшити в n = 2,00 рази? У скільки разів слід збільшити опір середовища, щоб коливання стали неможливими?

Розв’язання.

Як відомо з теорії згасаючих коливань, логарифмічний декремент може

бути виражений формулою:					(1)
		λ = β T ,			(1)
де β − коефіцієнт згасання, T − період коливання,					який визначається
формулою β =	r	, де r − опір середовища. Отже можемо записати:
формулою β =	2m	, де r − опір середовища. Отже можемо записати:
	2m		r
		λ =	r	T .
		λ =	2m	T .
			2m

Відношення декрементів згасання того самого маятника в двох середовищах 2 і 1 таке:

	λ2	=	r2		T2	.	(2)
	λ		r
					T
1		1		1
Позначивши r2 r1 = n , запишемо:		= n T2 .
	λ2						(3)
	λ			T
1				1

З теорії згасаючого маятника відомо, що залежність його циклічної частоти ω від β виражається формулою:

ω 2 = ω 2	− β 2,	(4)
0

де ω0 − частота незгасаючих вільних коливань (власна частота). Узявши до уваги (1), останню рівність перепишемо так:

ω 2 = ω02 −	λ 2	, або, оскільки ω =			2π	,	4π 2	= ω02 −	λ 2	, нарешті,
	T 2				T		T 2		T 2
			1	(4π 2			+ λ 2 )= ω02.			(5)
			2	(4π 2			+ λ 2 )= ω02.			(5)
			T

Таким чином, ми бачимо, що вираз T12 (4π 2 + λ 2 ) є інваріантною

величиною, тобто такою, що не залежить від середовища. Тепер можемо записати:

(4π 2 + λ12 )=

(4π 2 + λ22 ),

T 2

звідки

2 + λ 2

4π

T 2

2 + λ 2

або, зважаючи на (2),

4π 2 + λ 2

1 λ

2 ,

4π 2 + λ 2

n2 λ

звідки неважко дістати:

а) λ2 =

nλ1

= 3,3 .

1 − λ12

(n2 − 1) 4π 2

б) Коливання стануть неможливими при

λ2 = ∞ , або коли знаменник

рівний нулю:

1 − λ12 (n2 − 1)

4π 2 = 0 ,

звідки можна знайти

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.05.20151.34 Mб194Metodichni_vkazivki_elektronika_2012.docx
#
12.05.20151.93 Mб15Metodichni_vkazivki_Informatika.doc
#
12.05.2015246.78 Кб10Metodichni_vkazivki_kursova.doc
#
12.05.2015629.56 Кб14metodIII.pdf
#
12.05.20155.58 Mб10metoditnew.pdf
#
12.05.2015957.22 Кб83MetodMechanics (1).pdf
#
25.11.2019587.26 Кб1MetodRekomKKP-Zakharchenko(2)_Paltsun(1)_Brukva...doc
#
12.05.20153.67 Mб22Metodychka_OS_labs_2012.doc
#
12.05.20151.78 Mб13metodychka_os_labs_2012.pdf
#
12.05.20151.7 Mб8metod_1.pdf
#
12.05.20152.85 Mб7metod_2.pdf