§ 3. Асимптотические оценки (два примера) 23

при этом из v(n) = о(п²) не следует, что v(n) = 0(п), что доказывается примером v(n) = n^3/2.

Слова «(п) имеет асимптотику g(n)» означают, что /(n)~g(n); например, 7} (п) имеет асимптотику п², а 7} (п) имеет асимптоти­ку ¹₂п².

Сложности многих алгоритмов трудно или невозможно предста­вить элементарного вида функциями от размера входа. Помимо это­го, точное значение сложности алгоритма для каждого конкретно­го значения размера входа часто не представляет особого интереса, актуальным же является исследование роста сложности при возрас­тании размера входа. Поэтому асимптотическое оценивание широко используется в теории сложности.

§ 3. Асимптотические оценки (два примера)

Если мы изначально имеем эскизное описание алгоритма, не содер­жащее мелких деталей, но полностью отражающее его идею, то уже этого эскиза может быть достаточно для получения некоторой инфор­мативной асимптотической оценки сложности; проработка деталей алгоритма будет влиять на скрытые за символами О, Г2, в значения констант.

Пример 3.1. Займемся задачей построения выпуклой оболочки ко­нечного множества М точек координатной плоскости, т. е. выпуклого многоугольника Я, содержащего все множество М (рис. 1). Множест-

а) б)

Рис. 1. a) Конечное множество М точек плоскости; б) выпуклая оболочка множества М.

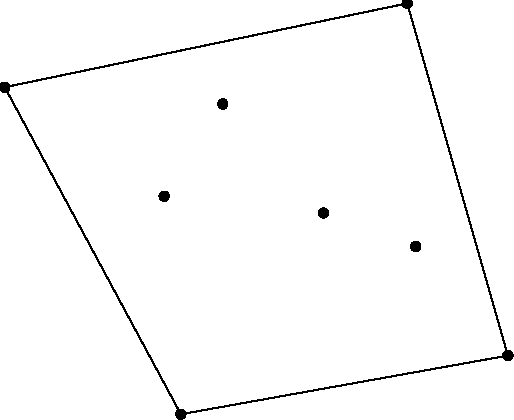
во М задается массивом координат принадлежащих ему точек; тре­буется построить массив координат вершин многоугольника Я при обходе этого многоугольника, начиная с какой-нибудь его вершины,

24 Глава 1. Сложности алгоритмов как функции числовых аргументов

против часовой стрелки (считаем, что это направление совпадает с направлением обхода точек (0,0), (1,0), (0,1), (0,0)).

Пусть n—число элементов множества M, будем считать это чис­ло размером входа. Алгоритм, основанный на переборе всех под­множеств множества M с проверкой для каждого из них, являет­ся ли оно множеством вершин искомого многоугольника H, имеет очень высокую сложность Ω(2n). Обсудим идею значительно более экономного алгоритма Р.Л.Грэхема (этот алгоритм мы обозначим буквой G).

Можно довольно быстро найти среди точек множества M такую, которая обязательно будет одной из вершин многоугольника H: до­статочно выбрать в M точку P с наименьшей ординатой, а если таких точек несколько, то из этих нескольких взять ту, которая имеет наи­меньшую абсциссу. Дополнительно найдем точку O, которая принад­лежит многоугольнику H, но не совпадает ни с одной из точек мно­жества M: возьмем для этого какие-нибудь две точки из M и найдем середину соединяющего их отрезка (если впоследствии вдруг окажет­ся, что эта точка принадлежит M, то можно будет удалить ее из M, так как она заведомо не является вершиной H).

Используя какую-нибудь сортировку с помощью сравнений, все точки множества M можно упорядочить по возрастанию углов между отрезком OP и отрезками, соединяющими O с точками множества M, при этом мы считаем, что величина каждого угла принадлежит полу­интервалу [0, 2тг). Если вдруг обнаружится, что два каких-то угла рав­ны, то упорядочим соответствующие точки по удаленности от O, но для краткости будем говорить просто о сортировке по величине угла. Соединив точки в этом порядке (будем обозначать их P_ъ P₂,..., P_n, при этом P_г = P), и соединив дополнительно P_n c P_г, мы получим замкну­тую несамопересекающуюся ломаную, но ограниченный этой лома­ной многоугольник может не быть выпуклым (см. рис. 2а). Тогда сре­ди вершин P₂,P₃, ...,P_n найдется хотя бы одна, скажем P_k , вдавленная, которая принадлежит треугольнику P_k-_гOP_k+1 при k < n и треуголь­нику P_n-₁OP₁ при k = n (рис. 2б). Вдавленную вершину можно исклю­чить из дальнейшего рассмотрения, соединив напрямую P_k-_г с P_k+1, или, соответственно, P_г с P_n-_г. Удалив все вдавленные вершины, мы получим требуемый многоугольник. Такова общая идея алгоритма. Задержимся на удалении вдавленных вершин.

¹ «Наглядно можно представлять себе дело так: в точках M вбиты гвозди, на кото­рые натянута резинка, охватывающая их все, — эта резинка и будет выпуклой оболоч­кой множества гвоздей» [21]. Но в нашем понимании построение выпуклой оболочки предполагает еще перечисление вершин в порядке их обхода.