
labor-ts
.pdfПопытаемся при определении суммарных баллов каждого участника принять во внимание результаты других участников.
Вычислим новый вектор a2 следующим образом: к баллам каждого участника прибавим баллы тех, с кем он сыграл вничью, и удвоенное число баллов тех, кого он победил:
|
|
|
|
3 + 0 + 2 7 |
|
17 |
|
|
|
|
|
|
7 + 0 + 2 15 |
|
|
|
|
|
2 |
|
|
|
|
37 |
||
a |
= |
|
6 + 4 +16 |
|
= |
|
|
|
|
|
|
26 |
|||||
|
|
|
|
4 + 6 + 2 3 |
|
|
16 |
|
|
|
|
|
5 + 0 + 2 7 |
|
|
|
|
|
|
|
|
|
|
19 |
. |
|
Теперь последним оказался участник 4, а участник 1 оказался на четвертом месте. Продолжим эту процедуру:
|
|
|
|
|
17 + 2 37 |
|
|
91 |
|||
|
|
|
|
|
+ 2 (26 +16 |
+ |
|
|
|
|
|
|
3 |
|
37 |
19) |
|
159 |
|||||
a |
= |
|
26 |
+16 + 2 (17 |
+ |
|
= |
|
|
|
|
|
|
19) |
114 |
||||||||
|
|
|
|
|
16 + 26 + 2 |
17 |
|
|
76 |
|
|
|
|
|
|
|
|
|
|
|
|
85 |
|
|
|
|
|
|
19 + 2 (17 + 6) |
|
|
. |
|||
Теперь участник 1 оказался на третьем месте.
Для a4 получим: a4 = (409, 709, 542, 372, 419)T и порядок мест (4 1 2 5 3), т.е. участник 1
оказался снова на четвертом месте.
Для a5 = (1827, 3375, 2149, 1732, 1981)T получим порядок мест (4 1 2 5 3), т.е. тот же результат. Таким образом, распределение мест участников стабилизировалось.
Возьмем нормированные векторы:
a4 = (0,167; 0,289; 0,221; 0,152; 0,171)T , a5 = (0,164; 0,304; 0,198; 0,156; 0,178)T .
Дальнейшие итерации выполняются аналогично вплоть до того момента, когда вектор ai перестанет изменяться. Окончательный вектор a принимается за вектор относительных весов альтернатив, а его компоненты, упорядоченные по убыванию значений, определяют итоговое ранжирование альтернатив по важности.
Какими же свойствами обладает найденный вектор a?
Рассмотренный рекуррентный процесс можно записать следующим образом: at = B at−1, a0 = (1, 1, 1, 1, 1)T .
С учетом нормировки, где n = 5 − число участников, получим:
at |
= |
1 |
B at−1 |
, где |
|
λt |
|||||
|
|
|
|
||
|
|
n |
n |
|
|
λt |
= ∑∑bi j atj−1 – сумма компонент вектора B at−1 . |
||||
|
|
i=1 j=1 |
|
||
|
n |
|
|
|
|
Поэтому |
∑atj =1, |
t > 0 . |
|||
j=1
21
Из линейной алгебры хорошо известно, что данный процесс сходится к собственному вектору, соответствующему максимальному собственному числу линейного преобразования В. Известно, что квадратная матрица В ранга n имеет n различных собственных чисел, вообще говоря, комплексных. Данная матрица содержит только неотрицательные элементы, поэтому ее максимальное собственное число λmax всегда положительно.
Условием сходимости данного процесса к собственному вектору, соответствующему максимальному собственному числу, является неразложимость квадратной матрицы В. Квадратная матрица В называется разложимой, если множество индексов I = {1,…, n} можно
разбить на два подмножества I1 и I2 так, что bi j = 0 для всех пар (i, j), где i I1 , j I2 .
Другими словами, столбцы и строки матрицы В можно одновременно переупорядочить так, что мы получим матрицу со структурой следующего вида:
1 … n
|
I1 |
B11 |
0 |
1 |
|
B = |
|
||||
I2 |
B21 |
B22 |
n |
||
|
|||||
|
|
I1 |
I2 |
||
|
|
|
Разложимость матрицы В означает, что в данном случае все альтернативы из I2 предпочтительнее всех альтернатив из I1.
Отметим, что при проведении экспертизы часто возникает проблема оценивания компетентности экспертов. В этом случае «задача о лидере» рассматривается как задача оценки компетентности экспертов на основе взаимооценок, когда каждый из экспертов оценивает других. В частности, разложимость матрицы взаимооценок В означает, что все эксперты из I2 считают некомпетентными всех экспертов из I1. Это свидетельствует о серьезных разногласиях среди экспертов, т.е. их общее мнение не является согласованным.
В этом случае необходимо либо сформировать другую группу экспертов, либо применить процедуру взаимооценки отдельно в каждой подгруппе.
Содержание отчета
Отчет должен содержать:
-цель выполнения работы,
-описание всех необходимых этапов выполнения работы и все необходимые расчеты,
-выводы.
Контрольные вопросы
1.Что такое турнирная таблица?
2.Как получить турнирную таблицу из матрицы попарных сравнений альтернатив по важности?
3.Что такое собственный вектор и собственное число линейного преобразования?
4.Какая матрица B является разложимой?
5.Что означает разложимость матрицы B?
6.Как получить общее ранжирование альтернатив по важности?
22
Лабораторная работа № 6. Оценка компетентности экспертов по результатам экспертизы
Цель работы
Изучить метод получения ранжирования экспертов по компетентности на основе степени согласованности мнения каждого эксперта с мнением большинства.
Порядок выполнения работы
1.На основе сравнений по принципу Борда альтернатив по важности, полученных в лабораторной работе №1, оценить компетентность экспертов, рассматривая степень согласованности мнения каждого из них с мнением большинства.
2.Оценить компетентность экспертов итерационным методом.
3.Оценить компетентность экспертов как собственный вектор, соответствующий максимальному собственному числу специальной матрицы, построенной из таблицы сравнений альтернатив по важности по принципу Борда.
4.Сравнить полученные результаты.
5.Изучить литературу: [3]: стр.77-81; [11]: 159-165, 171-174.
Методические указания
Построенную по принципу Борда табл. 4 в лабораторной работе №1 представить в данной работе в виде табл.1 размером n × N, где N столбцов представляют мнения экспертов, а n строк представляют альтернативы в исходном порядке. В каждом столбце табл.1 элементы представляют номера альтернатив в ранжировке соответствующего эксперта: последней по предпочтению альтернативе присваивается 1, предпоследней – 2 и т.д.:
|
|
|
Таблица 1. |
|
|
|
|
||
Альтернативы |
Эксперты |
|
||
1 2 |
... j |
... N |
||
|
||||
a1 |
. . |
k |
. |
|
a2 |
. . |
n |
. |
|
. |
. . |
. |
. |
|
ai |
. . |
1 |
. |
|
. |
. . |
. |
. |
|
an |
. . |
n-1 |
. |
|
Например, в j-ом столбце альтернатива ai является последней в ранжировке j-го эксперта, поэтому ей присвоено наименьшее число 1 вместо 0, по сравнению с принципом Борда в лабораторной работе №1. Это сделано для того, чтобы не получить строку, состоящую полностью из нулей, если, например, все эксперты признают альтернативу ai наименее предпочтительной среди всех остальных.
Обозначив табл.1 как матрицу X, вычислить матрицу X ТX и найти ее собственный вектор, соответствующий ее максимальному собственному числу. Поиск собственных чисел и
23

собственных векторов матрицы X ТX выполнить средствами подходящей программы
(MathCAD, MathLAB).
Теоретические сведения
В данном подходе реализуется идея о том, что компетентность эксперта определяется степенью согласованности его мнения с мнением большинства.
Пусть дана таблица Х мнений трех экспертов о распределении ресурсов (капитальных вложений) между двумя проектами:
|
эксперты |
|
сумма |
среднее |
|
||||
Проект 1 |
0,8 |
0,4 |
0,7 |
1,9 |
1,9 |
= 0,63 |
|
||
|
|
|
|
|
|
3 |
|
||
|
|
|
|
|
|
|
|
||
Проект 2 |
0,2 |
0,6 |
0,3 |
1,1 |
1,1 |
= 0,37 |
|
||
|
|
|
|
|
|
3 |
|
, |
|
|
|
|
|
|
|
|
|||
где N = 3 – число экспертов, n = 2 – число проектов.
Предположим, что эксперты одинаково компетентны и вычислим средние оценки проектов: x1 = (0,63; 0,37)T . Мы получим этот вектор в результате операции:
x1 = X a0 , где a0 = (1/ 3, 1/ 3, 1/ 3)T ,
где X – матрица экспертных оценок размером n × N , а – вектор оценок компетентности.
Пересчитаем компетентность экспертов с учетом средних оценок проектов x1. Для этого просуммируем оценки экспертов с весами, заданными оценками проектов x1:
|
|
a1 |
0,8 0,63 + 0,2 0,37 |
|
|
0,58 |
|
|||
a |
1 |
11 |
|
|
0,63 |
|
|
|
|
|
|
= a2 |
|
= 0,4 |
+ 0,6 0,37 |
= 0,47 |
|
||||
|
|
1 |
|
|
0,63 |
+ 0,3 0,37 |
|
|
|
, |
|
|
a3 |
|
0,7 |
|
|
0,55 |
|||
где сумма компонент вектора а1 составляет 1,6. Тем самым мы выполним операцию: a1 = X T x1 = X T X a0 .
Возьмем нормированный вектор:
a1 = 11,6 (0,58; 0,47; 0,55)T = (0,36; 0,3; 0,34)T ,
т.е. выполним операцию:
|
1 |
|
n |
N |
|
a1 = |
X T X a0 , где λ1 |
= ∑∑xij x1j . |
|||
1 |
|||||
|
λ |
|
i=1 |
j=1 |
|
Очевидно, что больший вес получит тот эксперт, который выше оценил проект, набравший наибольшее число баллов. С учетом новых весов экспертов получим новые оценки проектов:
x2 = X a1 = (0,65; 0,35)T
и т.д., до того момента, когда векторы а и х перестанут изменяться.
24
Данный итерационный процесс может быть представлен в следующем виде:
|
xt |
= X at−1 |
|
|
|
|
||||
(1) |
|
|
|
1 |
|
|
|
|
|
где |
|
t |
|
|
T |
|
t |
, |
|||
|
a |
= |
|
X |
x |
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
λt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t > 0, a0 = (1/ n, 1/ n, 1/ n)T , λt |
n |
N |
= ∑∑xij xtj |
||
|
i=1 |
j=1 |
Или, что то же самое:
|
|
t |
|
|
|
1 |
|
|
|
|
T |
|
t−1 |
|
|
|
x |
|
= |
|
|
|
|
XX |
|
x |
|
|
|||
|
|
λ |
t−1 |
|
|
|
|
||||||||
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
t |
|
|
|
|
|
T |
|
|
t−1 |
|
|||
|
a |
|
= |
|
|
|
X |
|
Xa |
|
|
. |
|||
|
|
|
λ |
t |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это означает, что вычисления (1) фактически соответствуют двум параллельным процессам (2). Аналогично тому, что было показано в лабораторной работе №5, в каждом из этих процессов имеется собственный вектор, соответствующий максимальному собственному числу матриц XX T и X TX .
Условием сходимости данных процессов также является неразложимость матриц XX T и X TX. Выясним, какова для этого должна быть прямоугольная матрица X.
Прямоугольная неотрицательная матрица Х разложима, если путем одновременных перестановок всех строк и столбцов ее можно привести к виду:
|
|
1 |
|
N |
|
1 |
X |
11 |
0 |
|
|
X = |
|
|
X 22 |
|
|
n |
|
0 |
. |
||
|
|
|
|
|
|
Это означает, что эксперты и проекты распадаются на две несвязанные группы, где каждая группа экспертов оценивает только «свою» группу проектов.
Можно показать, что матрицы XX T и X TX неразложимы, если неразложима матрица X.
Содержание отчета
Отчет должен содержать:
-цель выполнения работы,
-описание всех необходимых этапов выполнения работы и все необходимые расчеты,
-выводы.
Контрольные вопросы
1.В чем состоит идея оценки компетентности экспертов?
2.Как получить матрицу X по принципу Борда?
3.Как получить матрицу X по стандартизированным рангам?
4.Что такое собственный вектор и собственное число линейного преобразования?
5.Какая матрица X является разложимой, что это означает?
6.Как получить общее ранжирование альтернатив по важности?
25
Лабораторная работа № 7. Принятие решений на основе функции полезности
Цель работы
Ознакомиться с понятием функции полезности и простой лотереи. Рассмотреть принципы участия игрока в лотерее с точки зрения теории полезности и их применение в задаче страхования.
Порядок выполнения работы
1.Выбрать событие (вид страхового случая), от нежелательных последствий наступления которого страховая фирма предлагает застраховать клиента.
2.Определить размер страховки, которая выплачивается фирмой клиенту в случае наступления нежелательных последствий страхового случая, и определить вероятность наступления страхового случая.
3.Построить функцию полезности страховой компании.
4.Определить страховой взнос клиента, функцию полезности клиента и минимальное число договоров страхования, чтобы обеспечить выплату страховки при наступлении одного реального страхового случая.
5.Изучить литературу: [13]: стр.17-25; [14]: 92-106.
Методические указания
Необходимо выбрать вид страхового случая. Например:
-катастрофы: транспортные, техногенные, экологические и т.д;
-природные явления: землетрясения, смерчи, наводнения и т.д;
-экономические события: банкротство, падение курса валюты и другие форс-мажорные обстоятельства;
-маловероятные и фантастические события: наводнение в пустыне, столкновение с космическим телом, интервенция пришельцев, восстание компьютеров и т.д.
Члены бригады, выступая как страховая фирма, определяют характеристики ее деятельности, согласно порядку выполнения данной лабораторной работы. Члены другой бригады выступают как клиенты, которым предлагают заключить договор страхования.
Теоретические сведения
Теория выбора в соответствии с полезностью является одним из подходов к изучению проблемы выбора в целом и основана на субъективности принимаемых решений (именно это всегда имеет место в жизни). Основной характеристикой принимаемого решения считается его так называемая «полезность». В данном разделе теории выбора разрабатываются рекомендации по выбору, которые не противоречат здравому смыслу в простых случаях и на которые можно опереться в сложных случаях, когда здравый смысл, подсказывающий «полезность» решения, может подвести.
Обычно причины возникновения такой ситуации заключаются в том, что индивидуальному выбору и предпочтениям присуща внутренняя противоречивость, которая может и не
26
осознаваться экспертом (ЛПР – лицо, принимающее решение) и не проявляться в простых случаях. Но в сложных случаях эта противоречивость может сделать невозможным принятие хоть какого-нибудь разумного решения.
В качестве одной из основных задач в теории выбора в соответствии с полезностью рассматривается выявление противоречий в предпочтениях ЛПР для осознанной коррекции экспертом своих предпочтений с целью устранения таких противоречий в реальных исследованиях. Следуя рекомендациям теории, ЛПР должен всегда выбирать альтернативу с максимальной ожидаемой полезностью.
Предпочтения и их полезность. Относительно предпочтений предполагается, что любую пару альтернатив можно сравнить по степени их предпочтительности, и все такие сравнения транзитивны. Таким образом, транзитивно упорядоченное множество альтернатив образует цепочку и не содержит циклов, т.е. оно линейно упорядочено.
Предполагается, что степень предпочтительности альтернативы x можно оценить неотрицательным числом u(x). Таким образом, значения u(xi), i = 1,…, n на множестве транзитивно упорядоченных альтернатив образуют некоторую функцию. Функция u(x) называется функцией полезности для предпочтений на альтернативах xi, i = 1,…, n, если для каждой пары xi и xj, где xi x j , выполнено условие u(xi ) > u(x j ) .
Предполагается, что значения функции полезности измеряются в интервальных шкалах (как шкалы температур). Поэтому по отношению к функции полезности u(x) допустимы линейные преобразования вида v(x) =αu(x) + β , α > 0 . Эквивалентность функций полез-
ности u(x) и v(x) относительно такого преобразования означает, что решения, принятые на их основе, также эквивалентны.
Часто предполагается, что с каждой альтернативой x связана вероятность ее появления p(x). Таким образом, на множестве альтернатив оказывается заданным некоторое множество P вероятностных распределений
(p j (x ),..., p j (x |
n |
))= (p j ,..., p j ), j =1,..., K , |
|
1 |
1 |
n |
|
где K – некоторое число распределений.
Рассматривая альтернативу x и функцию полезности u(x) как случайные величины U и X, определим среднюю полезность как матожидание случайной полезности:
n
E(U | X ) = ∑p(xi )u(xi ) .
i=1
Следовательно, задавшись некоторым распределением вероятностей на множестве альтернатив, можно судить об их средней полезности, т.е. судить о полезности некоторого распределения вероятностей.
Средняя полезность дает возможность сделать выбор среди альтернативных распределений вероятностей, т.к. на практике часто приходится делать выбор в условиях неопределенности относительно возможности существования тех или иных альтернатив.
Простая лотерея. Рассмотрим две альтернативы x1 и x2 с вероятностями их наступления p и 1– p. Пусть на альтернативах задано предпочтение x1 x2 и функция полезности
u(x1 ) > u(x2 ) . Средняя полезность определяется как
E(U | X ) = pu1 + (1− p)u2 , где u1 = u(x1 ), u2 = u(x2 ) .
Выполним над функцией полезности u(x) допустимые преобразования вида αu + β , где α =1, β = −u2 . Получим эквивалентную функцию полезности, представленную двумя
27
значениями (u1 −u2 , 0), где u1 −u2 > 0 , так как u1 > u2 . Снова выполним преобразование αu + β , где α =1/(u1 −u2 ) , β = 0 . Окончательно получим эквивалентную функцию полезности (1, 0). Определим для нее среднюю полезность E(U | X ) = p 1+ (1− p) 0 = p .
Таким образом, ожидаемая полезность равна вероятности появления альтернативы с ненулевой полезностью.
Если альтернативу x1 рассматривать как выигрыш в лотерее некоторой суммы, а альтернативу x2 – как безрезультатный исход, то такая система альтернатив называется простой лотереей с вероятностью выигрыша p. Эта вероятность определяет так называемый порог безразличного отношения к лотерее. Очевидно, что чем больше величина p, тем менее безразличны окружающие к участию в такой лотерее. Возникает вопрос: когда некоторый индивидуум примет участие в лотерее?
Рассмотрим три альтернативы |
x1, |
x2 и x3, где x1 – выигрыш, x3 – безрезультатное уча- |
стие. Тогда очевидно, что x1 |
x2 |
x3 , так как альтернатива x2 является промежуточной |
(получение некоторого промежуточного дохода, частичный выигрыш). Очевидно, что их полезность оценивается индивидуумом как u1 > u2 > u3 . Полезность лотереи u(x) является
линейной функцией, т.к. u(x1 ) =1, u(x3 ) = 0 , u(x2 ) = pu(x1 ) + (1− p)u(x3 ) = p , 0 ≤ p ≤1.
Функция полезности самого индивидуума имеет вид 1 >α > 0 , где α – полезность альтернативы x2.
Если функция полезности индивидуума также линейна (α = p ), то он останется равно-
душным к лотерее. Если его оценка полезности промежуточного дохода ниже предлагаемой лотереей полезности (α < p ), то данная лотерея для него более предпочтительна, чем
другая, в которой его оценка полезности выше, чем ему предлагают (α > p ). Поэтому он
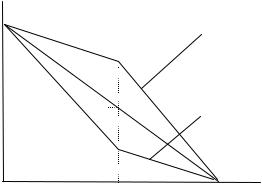
примет участие в первой лотерее и откажется участвовать во второй. Различные виды индивидуальных функций полезности показаны на рисунке. В первом случае (α < p ) функ-
ция полезности индивидуума является выпуклой и соответствует игроку, стремящемуся к риску. Во втором случае (α > p ) функция полезности индивидуума является вогнутой и
соответствует игроку, избегающему риска.
Опыт показывает, что функции полезности большинства людей, как правило, вогнуты.
u
Вогнутая функция полезности (игрок, избегающий риска)
α2 




















p


















α1 


















x1 |
x2 |
Выпуклая функция полезности (игрок, стремящийся к риску)
x
x3
28
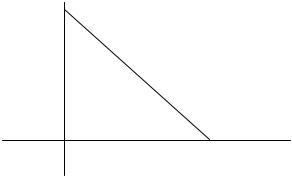
Задача страхования. Пусть, например, клиент полагает, что может в течение какого-то срока потерпеть убыток h =10000 руб. Клиент хочет возместить потери в случае реального наступления катастрофы. Это означает, что он не хочет принимать участие в простой лотерее вида:
полезность u(10000) =1
u(0) = 0
10000 |
0 |
h убытки |
(катастрофа) (норма)
Его отказ заключается в том, что он хочет гарантированно потерять некоторую сумму, например, x = 500 руб., для того, чтобы, возможно, не потерять 10000 руб. Как мы знаем, отказ от участия в такой лотерее означает, что функция полезности клиента вогнута, по сравнению с линейной функцией полезности данной лотереи. Степень вогнутости определяется суммой x = 500 руб. Отказ же от участия в лотерее означает заключение договора на страховку. В этом случае клиент предпочитает гарантированно потерять x = 500 руб. и возвратить h − x = 9500 руб. в случае катастрофы.
В отличие от клиента, страховая компания знает вероятность ε <<1 наступления катастрофы данного вида, т.е. вероятность страхового случая. Пусть, например, она составляет ε = 0,01 в течение страхового периода. Следовательно, компания определяет, что клиент
не хочет участвовать в лотерее со средним проигрышем ε h + (1 − ε) 0 =100 руб. Это
также выражается в том, что функция полезности клиента действительно оказывается вогнутой для x = 500 руб. Действительно, «полезность» проигрыша 500 руб. определяется из условия u h + (1 − u) 0 = 500 , т.е. u = 500 / h = 0,05 .
Если договор будет заключен, то компания получит чистый доход в течение страхового срока x −ε h = 500 −100 = 400 руб. Очевидно, что при выполнении обоих этих условий договор будет заключен.
Откуда же возьмутся 10000 руб. у компании в случае реального наступления страхового случая? Например, для этого ей надо заключить h / x =10000 / 500 = 20 договоров. Естественно, надо быть уверенным, что страховые случаи не наступят одновременно у некоторого максимально допустимого числа клиентов. В противном случае страховая фирма разорится. Например, это произойдет в случае глобальной катастрофы, или локальной, но затрагивающей интересы одновременно некоторой достаточно большой части клиентов страховой компании.
29
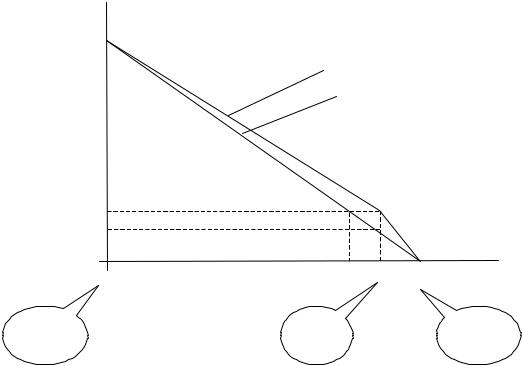
полезность
u(10000) =1
клиент
страховая компания
u(500) |
= 0.05 |
|
|
u(100) |
= 0.01 |
|
|
u(0) = 0 |
500 100 |
|
|
|
10000 |
0 убытки |
|
катастрофа с |
средний |
Норма с |
|
вероятностью |
ожтдаемый |
вероятностью |
|
ε << 1 |
|
проигрыш |
1-ε >> 0 |
Содержание отчета
Отчет должен содержать:
-цель выполнения работы,
-описание всех необходимых этапов выполнения работы и все необходимые расчеты,
-выводы.
Контрольные вопросы
1.Что такое функция полезности?
2.Что такое транзитивность предпочтений?
3.Что такое простая лотерея?
4.Что такое эквивалентное преобразование простой лотереи?
5.Что такое шкала?
6.Какие бывают шкалы?
7.Что такое средняя ожидаемая полезность?
8.Кто такой игрок, избегающий риска?
9.Кто такой игрок, стремящийся к риску?
10.Что такое задача страхования в теории полезности?
30
