
Конспект лекций Электродинамика и РРВ
.pdf
Фазовые скорости этих волн vф выше фазовой скорости v однородной волны в той же среде. Говорят, что это быстрые волны. Действительно, поскольку 0 < ϕ < 900, то при вещественном k = ω/v из (5) следует
Г < k, vф > v. |
(6) |
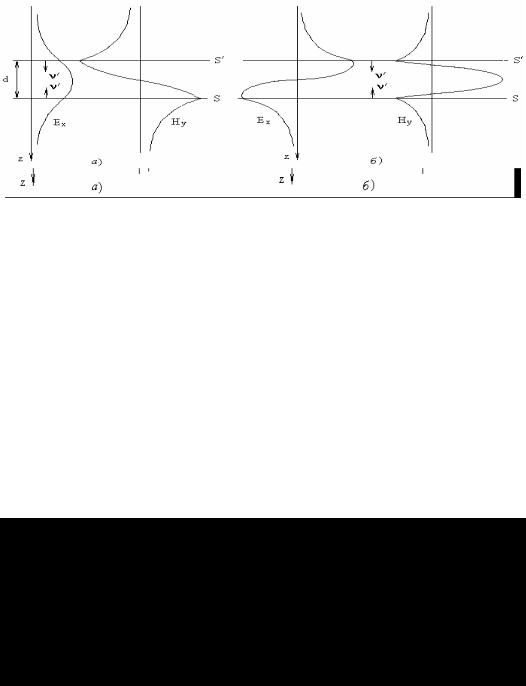
На рис.1а,б представлено распределение компонент векторов поля в плоскости фронта рассматриваемых неоднородных волн.
Рис.1. Распределение компонент полей
На расстояниях z = - nΛ /2 от границы раздела лежат плоскости, на которых выполняется условие Eτ = 0 и которые, следовательно, могли бы быть заменены идеально проводящими плоскостями без всякого нарушения структуры волн.
Если такую дополнительную идеально проводящую плоскость ввести, то между ней и первоначальной границей z = 0 образуется энергетически изолированный слой, внутри которого может существовать прежняя H– или E–
волна. Это простейший полый волновод.
Пусть расстояние между двумя рассматриваемыми плоскостями фиксировано и равно d. Наложим условие
χ = nπ d , n = (0),1,2,... |
(7) |
(n = 0 имеет смысл только в варианте параллельной поляризации). При подстановке nπ/d вместо величины χ = k*cosϕ в (2) и (5) на выделенной плоскости z = - d удовлетворяется граничное условие Еτ = 0.
Это значит, что для плоского волновода существует бесконечная последовательность значений χ, при которых в этой структуре могут распространяться H- и E–волны.
При этом волновой процесс в обычном смысле возможен лишь при достаточно высоких частотах. Действительно, исходя из (5), при подстановке значений χ в (7), получаем
Г = k 2 −(n π d )2 = k 1−(ωкр ω)2 , |
(8) |

где ωкр = (c εµ)(nπ d ) |
называется |
критической |
(круговой) частотой. При |
||||||||||||
вещественных ε, µ |
|
|
|
|
|
|
|
|
|
cos(ωt − Гy ),ω> ωкр; |
|||||
|
( |
−iГy |
) |
|
( |
iωt |
) |
|
|||||||
exp |
= |
|
(9) |
||||||||||||
Re exp |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
e |
|
Г |
|
y cosωt,ω< ω , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
кр |
||||
поскольку с понижением частоты при прохождении точки ω = ωкр постоянная распространения Г становится часто мнимой. Фазовое запаздывание, свойственное обычной волне, исчезает, и процесс экспоненциально затухает (в направлении y и – y).
На рис.2 показано распределение компоненты Ez(Ey) в плоскости фронта направляемой волны при перпендикулярной (параллельной) поляризации для разных n. Это, как говорят разные типы волн.
Рис.2. Распределение электрических компонент различных типов волн
Чем меньше n, тем ниже критическая частота; она обращается в нуль при n = 0. В этом единичном случае распространяется плоская однородная волна, лишенная продольной компоненты поля.
Вычислим фазовую скорость направляемой волны
vф = ω Г = ω k sin ϕ= v sin ϕ |
(10) |
и ее групповую скорость |
|
|
|
vгр = dω dГ = |
d |
(vГsin ϕ)= vsin ϕ, |
(11) |
|
dГ |
|
|
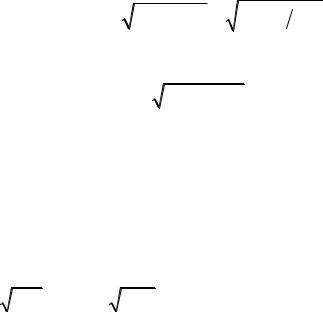
причем vфvгр = v, sin ϕ= 1−(ωкр 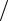 ω)2 .
ω)2 .
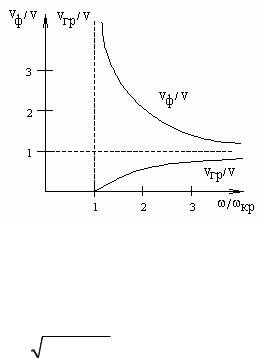
Рис. 3. Частотные зависимости фазовой и групповой скоростей волн
На рис.3 представлены частотные зависимости обеих скоростей.
При полном отражении от оптически менее плотной среды также формируется волна, направляемая границей раздела. При ϕ > ϕ* независимо от по-
ляризации sin ϑ >1, cosϑ = 1−sin2 ϑ величина мнимая. Это значит, что фор-
мулы Френеля для ρ|| и ρ принимают вид выражений (P - iQ)/(P + iQ), где P и Q при отсутствии поглощения вещественны. Поэтому модули ρ|| и ρ равны единице, и можно записать:
ρ |
|
= eiψ , |
ρ |
= eiψ| | . |
(12) |
|
|
| | |
|
|
Построим электромагнитное поле при полном отражении от границы раздела диэлектриков.
Перпендикулярная поляризация. В первой среде (z < 0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ |
|
|
|
|
|
ψ |
|
|
|
||||
Em = x0 A e |
−ikz cos ϕ |
+ e |
iψ |
e |
ikz cos ϕ |
e |
−iky sin ϕ |
= x0 2Acos kz cosϕ+ |
|
|
−i ky sin ϕ− |
|
|
, |
|
|
||||||||||||||||||||||||||||||||||||||||||
e |
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
A |
|
|
|
|
|
|
|
|
−ik1z cos ϕ |
|
iϕ |
|
|
ik1z cos ϕ |
|
|
|
|
|
|
|
|
−ik1z cos ϕ |
|
|
iψ |
|
|
ik 1 z cos ϕ |
|
|
−ik1y sin ϕ |
|
||||||||||||||||||||||
Hm = |
|
|
y0 cosϕ |
(e |
|
|
|
|
|
|
|
|
|
− e |
|
|
|
e |
|
|
|
|
|
|
)− z0 sin ϕ(e |
|
+ e |
|
|
e |
|
|
|
) e |
|
|
|
= (13) |
||||||||||||||||||||
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ |
|
|
|
|
|
|
|
ψ |
|
|||||
|
|
−y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−i k1 y sin ϕ− |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= 2 |
|
|
|
i cosϕsin |
|
k z cosϕ+ |
|
|
|
|
|
|
− z |
0 |
sin ϕcos |
|
k z cosϕ+ |
|
|
|
|
e |
|
|
|
2 |
. |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Во второй среде (z > 0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
E |
m |
= x |
|
τ |
|
Aexp −ik |
2 |
(ysin ϑ+ z cosϑ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(14) |
||||||
|
|
|
|
|
H |
|
= τ |
|
|
|
A |
|
( |
y |
|
|
cosϑ− z |
|
|
sin ϑ |
) |
exp |
−ik |
|
( |
ysin ϑ+ z cosϑ |
. |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
m |
|
|
|
|
0 |
0 |
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поле в первой среде, как показывают формулы (13), есть плоская неоднородная волна, распространяющаяся в направлении y. В плоскости фронта y = const распределение поля имеет вид стоячей волны, которая несколько смещена по оси z, так что при z = 0 уже не выполняется условие Eτ = 0.

Поле во второй среде есть продолжение неоднородной волны. Как видно из формул (13) и (14), продольные зависимости полей в обеих средах одинаковы:
Г = k1 sin ϕ = k2 sin ϑ. |
(15) |
Выясним, как распределено поле в плоскости фронта y=const во второй среде. Согласно (14) закон распределения имеет вид:
f (z)= exp(−ik2 z cosϑ)= e−iχ2 z ,
где введено поперечное волновое число для второй среды χ2, причем необходимо учесть, что cosϑ - мнимая величина ( поскольку sinϑ > 1). Запишем
|
|
2 |
|
|
|
|
|
|
|||
cosϑ = −i |
1− |
k1 |
sin ϕ |
|
|
= −i |
cosϑ |
, |
(16) |
||
|
|||||||||||
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. выберем при извлечении корня знак минус. Тогда |
|
||||||||||
f (z)= e−βz , |
β = k2 |
|
cosϑ |
|
. |
(17) |
|||||
|
|
||||||||||
Во второй среде (z > 0) поле экспоненциально убывает от границы раздела; говорят, что рассеиваемый процесс имеет здесь характер поверхностной волны. Очевидно, что выбор другого знака в (16) не был бы фактически оправдан.
Рис. 4. Распределение компонент поля неоднородной волны
На рис.4 показано распределение компонент векторов поля в плоскости фронта неоднородной волны в обеих средах: стоячая волна в первой среде переходит в поверхностную во второй.
Фазовая скорость рассматриваемой волны выше фазовой скорости однородной волны в первой среде v1 = c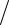 ε1µ1 , но ниже аналогичной величины
ε1µ1 , но ниже аналогичной величины
v2 = c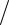 ε2µ2 для второй среды. В ней волна является, таким образом, медленной ( vф ≤ v2 ), будучи при этом поверхностной.
ε2µ2 для второй среды. В ней волна является, таким образом, медленной ( vф ≤ v2 ), будучи при этом поверхностной.

Аналогично рассматриваются поля в обоих средах в случае параллельной поляризации.
Поскольку cosϑ - мнимая величина, импеданс Z + или Z||+ для поверхностной волны – чисто мнимая величина. Введем понятие поверхностного импе-
данса ZS, который определяет соотношения Emτ, Hmτ на границе раздела сред
Emτ = ZS (Hmτ × ν′0 ). |
(18) |
Здесь ν0´ - орт внутренней нормали для первой среды: ν01 = -z01. Подставляя соответствующие выражения для полей, получим
|
|
|
x0 |
y0 |
z0 |
|
(−Hmy )+ y0 Hmx . |
−Hmτ ×z0 = − |
Hmx |
Hmy |
0 |
= x0 |
|||
|
|
|
0 |
0 |
1 |
|
|
−Z |
C |
cosϑ, |
H − волны |
|
|||
ZS = |
|
|
E − волны. |
|
|||
−ZL cosϑ, |
|
||||||
Поскольку cos ϑ = -i|cos ϑ|, можем утверждать, что ZS имеет емкостный характер для H–волн и индуктивный – для E–волн. Наличие такого поверхностного импеданса (поддерживаемого процессом в первой среде), можно рассматривать как условие существования поверхностной волны во второй среде.
Лекция № 13. Плоский диэлектрический волновод
Как и при полном отражении от идеально проводящей границы, в случае полностью отражающей границы диэлектриков тоже существуют плоскости, на которых Еτ = 0. Каждую такую плоскость можно заменить идеально проводящей границей, и в «отсеченном» диэлектрическом слое сохранится рассматриваемое поле. Поэтому ясно, что слой диэлектрика фиксированной толщины D, ограниченный с одной стороны идеально проводящей плоскостью, способен направлять различные волновые процессы. На рис.1 показано распределение компонент поля для двух таких волн а и б.
Рис. 1. Распределение компонент поля для слоя с экраном
Необходимые условие существования волн в этом слое, экранированном при z = -D, имеет вид:
Ех(-D) = 0, H–волны
Еу(-D) = 0, Е–волны (1)
В силу симметрии поля на выделенной в диэлектрике поверхности S’имеет место такое же соотношение тангенциальных компонент, как и на границе диэлектриков S. Поэтому ту часть структуры, которая лежит за этой плоскостью, можно отбросить, заменив полупространством с такими же свойствами, как и при z < 0. Тогда смогут существовать поля, показанные на рис.2. При этом внутри диэлектрического слоя на обеих его границах выполняются условия полного отражения для однородной волны.
Рис. 2. Распределение компонент поля для слоя без экрана
Каждая из этих границ является импедансной поверхностью, «поддерживающей» вне слоя поверхностную волну. Плоский диэлектрический слой выступает как волновод – структура, направляющая волновой процесс.
Поскольку критические частоты ω = ωкр(n) соответствуют условно ϕ = ϕ*,
при котором ϑ = 90о, то из формул Френеля следует ρ = ρ|| = 1, т.е. ψ = ψ|| = 0, При ϕ = ϕ* вне слоя в направлении y распространяется обычная волна, а следо-
вательно, на границе продольная компонента (Hy или Ey в зависимости от типа поляризации) утрачивается. Это будет, если
sin(k z cosϕ ) = 0, z = 0, z = −d . |
(2) |
1 |
|
При z = 0 это условие заведомо выполнено, а второе требование дает:
k1d cosϕ = nπ, n = 0,1,…, |
(3) |
||||
Учитывая, что |
|
|
|
|
|
cosϕ* = 1−sin2 ϕ* = |
1−(k2 k1 )2 , |
(4) |
|||
и ω = ωкр, получаем |
|
|
|
|
|
ω = nπ |
c |
|
. |
(5) |
|
|
|
||||
кр |
d |
ε1µ1 − ε2µ2 |
|
||
|
|
||||
Значение n = 0 относится к низшей Н–волне и низшей Е–волне. Рассматриваемый нами идеальный диэлектрический волновод в виде бес-
конечного слоя представляет собой хорошее приближение к некоторым пленочным волноводам, используемым в интегральной оптике. Для оптики, где частоты весьма велики, имеет важное значение тот факт, что даже в случае относительно толстой пленки (d >> λ) можно не допустить существования высших волн ( n ≥1). Для этого, как следует из (5), надо погрузить пленку в среду с близкой оптической плотностью. Чем ближе показатели преломления первой и
второй сред n1 = ε1µ1 и n2 = ε2µ2 , тем выше критические частоты. Если же
удалось выполнить условие ωкр(1) > ω, то в слое будет распространятся только низшая волна той или иной поляризации.
Действие проводящих границ
Согласно закону Снеллиуса при |k2| >> k1 при любом угле падения плоской волны в первой среде преломленная волна во второй среде распространяется почти по нормали, т.е. всевозможные поля в первой среде вызывают во второй среде процесс, близкий к плоской однородной волне, фронт которой параллелен границе. Когда вторая среда – проводник, этот процесс относительно быстро затухает, что называется поверхностным эффектом, а также скинэффектом. Расстояние ∆0, отсчитываемое по нормали в глубь проводника, на котором поле уменьшается в е раз:

∆0 = |
2 |
, |
(6) |
|
ωµ0µσ |
||||
|
|
|
Называется глубиной проникновения.
Рис. 3
Хотя подобные рассуждения относятся – в строгом смысле – к плоским границам, они применяются на практике к границам реальных проводящих тел пока все радиусы кривизны поверхности значительно больше глубины проникновения ∆0.
Пусть при выполнении этого условия некоторая проводящая оболочка (рис. 3б) ограничивает область V, в которой рассматривается поле Е и Н. Если оболочка не слишком тонкая (например, нигде не тоньше 10∆0), то ее поверхность S действует подобно границе сплошного проводника: волна, уходящая вглубь, затухает, «не успевая» дойти до внешней границы (от которой должно произойти отражение). Значит, влияние проводника здесь определяется лишь его границей и не зависит от занимаемого объема.
Таким образом влияние проводника во многих случаях можно учесть при помощи некоторого граничного условия. Поскольку тангенциальные компоненты векторов Е и Н на поверхности проводника непрерывно переходят в поперечные компоненты поля уходящей вглубь волны, соотношения между ними дается формулой
|
|
|
|
|
Еmτ = Zпр(Hmτ × ν'0 ), |
|
|
|
|
(7) |
|||||||
где ν0’ - орт внутренней нормали (ν0’ = z0), |
(1+ i) |
|
|
|
|
|
|||||||||||
|
|
|
µ |
µ |
|
|
µ |
µω |
i π |
|
|
|
|
|
|||
Z |
пр |
≈ |
0 |
|
|
= |
0 |
|
|
|
e 4 = |
|
= R |
+ iX |
пр |
, |
(8) |
|
|
|
|
|
|
|
|||||||||||
|
|
−i σ ωε0 |
σ |
|
|
σ∆0 |
пр |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
R |
= X |
пр |
=1 σ∆0 . |
|
|
|
|
(9) |
||||
|
|
|
|
|
|
пр |
|
|
|
|
|
|
|
|
|
|
|
Мы видим, что сформулировано импедансное граничное условие и Zпр
играет роль поверхностного импеданса. Равенство (7) называется приближен-
ным граничным условием Леонтовича.
Поскольку при σ→∞ волновое сопротивление Zпр исчезает, граничное условие Леонтовича в случае идеального проводника переходит в известное условие Еτ = 0.
Чтобы найти мощность, поглощаемую проводником, или мощность потерь Рп , надо вычислить входящий в него из внешней среды поток энергии.
Таким образом,
|
|
п = Re ∫Пv dS = −Re ∫Пv dS |
(10) |
|
Р |
||||
|
|
S |
S |
|
(ν’- направление внутренней нормали).
Ограничиваясь случаем сильного поверхностного эффекта, используем граничное условие Леонтовича. При этом
Пv ' = |
1 |
(Emτ ×Hmτ )v ' |
= |
1 |
(Zпр (Hmτ × ν'0 )×Hmτ ) |
|
= |
1+ i |
Hm2 |
τ |
||||||||||
Z |
2 |
v ' |
0 |
|||||||||||||||||
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2σ∆ |
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
Rпр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
||
|
|
Р = |
|
|
H |
dS = |
H |
dS . |
|
|
|
|
(11) |
|||||||
|
|
|
|
|
mτ |
|
mτ |
|
|
|
|
|||||||||
|
|
|
п |
2σ∆0 ∫S |
|
|
2 |
∫S |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Будем рассматривать ток в проводнике. Поскольку j = σE, плотность тока j, как и поле, быстро убывает в глубь проводника. Ток в реальном проводнике в случае сильного поверхностного эффекта удобно относить к линии, которую он пересекает на поверхности, т.е. удобно рассматривать как поверхностный. На рис. 4а линия l ортогональна направлению тока. Так ∆Im, проходящий через всю толщу проводника на участке ∆l, вычисляется как
∆Im = ∆l∞∫ jmdv' = ∆lσ∞∫Emdv',
0 |
0 |
где Em = Emτ exp(−ikv') . Поэтому согласно определению поверхностного тока
ηm = σEmτ ∞∫e−ikv 'dv' = −i |
σ Emτ . |
(12) |
0 |
k |
|
Рис. 4
Используя выражение для поверхностного импеданса проводника, а так-
же
k = ω ε |
µ |
0 |
(ε −iσ ωε |
0 |
) ≈ (1−i) |
ωµ µσ i = (1−i) ∆0 |
; |
0 |
|
|
|
0 |
|
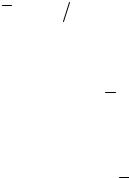
ηm =−i |
σEmτ =−i |
σZпр(Hmτ ×ν'0 )=Hmτ ×ν'0 =ν0 ×Hmτ. |
(13) |
|
k |
k |
|
Сопоставляя (11) и (7) видим, что |
|
||
|
|
Emτ = Zпрηm |
(14) |
Таким образом, поверхностный импеданс Zпр получает новую интерпре-
тацию.
Возвращаясь к выражению мощности потерь (11) и учитывая соотношение (13), получаем следующую формулу
|
|
п = |
1 Rпр ∫ηm2 dS . |
(15) |
|
Р |
|||||
|
|
|
2 |
S |
|
Если бы ток был равномерно распределен в слое глубиной ∆0, мы получили бы такой же результат. Дело в том, что Rпр есть сопротивление единичного квадрата проводящего листа толщиной ∆0 (рис.4б). Эти соображения поясняют смысл слов глубина проникновения.
Вычислим в качестве примера мощность потерь, отнесенную к единице
длины проводника pn = dPп |
dz . Проводник имеет поперечное сечение S с кон- |
|||||
туром l (рис. 4в). |
|
|
|
|
|
|
На отрезке проводника ∆z поглощается мощность |
|
|||||
|
∆ |
Pп = 12 Rпр ∫ηm2 dl ∆z. |
|
|
||
|
|
|
l |
|
|
|
Переходя к пределу при ∆z → 0 , находим |
|
|
||||
|
|
∆ |
Pп = 12 Rпр ∫ηm2 dl. |
|
(16) |
|
|
|
|
l |
|
|
|
Если можно говорить о падении напряжения на единицу длины провод- |
||||||
ника U’, то Um′ = Emz = Emτ |
- величина постоянная. Тогда согласно (12) посто- |
|||||
янна и плотность тока ηm . В этом случае из (14) получаем |
|
|||||
pn = 1 R′Im2 , |
|
R ' = Rпрl−1 = |
1 |
; Im = ηml , |
(17) |
|
|
σ∆0l |
|||||
2 |
|
|
|
|
|
|
где R ' - погонное сопротивление проводника, а l – длина контура l его поперечного сечения (рис. 4в).
