Конспект лекций Электродинамика и РРВ

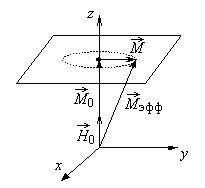
Лекция № 28. Распространение электромагнитных волн в гиромагнитных

средах (ферритах)

Ферриты – это ферромагнитные полупроводники и диэлектрики, обычная химическая формула которых MeOFe2O3 (Ме - двухвалентный металл).

Анизотропия феррита такая же, как и в плазме, создается постоянным или медленно меняющимся (по сравнению с полями распространяющихся в феррите волн) магнитным полем. При Н = 0 магнитная проницаемость феррита – скалярная величина.

Вообще говоря, такое представление является приближенным. Феррит имеет кристаллическую структуру, и реальным ферритам свойственна кристаллографическая анизотропия, т.е. зависимость магнитных свойств от направления намагничивания относительно осей кристаллической решетки. Однако учет кристаллографической анизотропии не меняет вида тензора магнитной проницаемости, а изменяет лишь его компоненты. Поэтому будем считать, что в отсутствие внешнего магнитного поля феррит является средой изотропной.

Нахождение компонент тензора основано на следующих представлениях. Как известно, молекулы феррита обладают магнитным моментом, имеющим спиновую природу. Структура феррита такова, что моменты отдельных молекул не компенсируются и единица объема среды обладает магнитным моментом М. Анизотропия создается прецессией магнитных диполей вокруг силовых линий магнитного поля.

Уравнение движения для М имеет вид

Рис.1. Ориентация векторов магнитного поля и намагниченности в феррите

Это – уравнение Ландау-Лифшица. Здесь Мэфф = М0 + М и Нэфф = Н0 + Н, γ = 2.21*105 (А/м)-1с-1 - постоянная, называемая гиромагнитным отношением, Н0 - постоянное поле, Н - поле волны, распространяющейся в феррите, М0 - постоянная намагниченность, совпадающая по направлению с Н0. Взаимное расположение векторов показано на рис.1.

Будем считать, что Н << H0 и M << M0. Тогда уравнение (1) примет вид

Предполагая гармоническую зависимость величин М, Н от времени, ~ exp(iωt ), и переходя к записи по компонентам, получим

Решая систему, найдем величины Mx, My, Mz. Обозначив Ω = γ|H0|, полу-

чим

Пользуясь материальным уравнением

B = µ0H + M,

расписываем его в виде системы уравнений для компонент

Таким образом, компоненты тензора µij принимают вид

Тензор магнитной проницаемости феррита имеет такой же вид, как и тензор диэлектрической проницаемости плазмы в магнитном поле. Тензор µˆ (ω) - эрмитов, т.е. феррит является магнитоактивной средой. Нормальные

волны должны иметь в феррите круговую или эллиптическую поляризацию. Компоненты тензора зависят от ω и от H0. При частоте ω, близкой к Ω, наблюдаются резонансные явления.

Линейно-поляризованная волна в продольно-намагниченном феррите расщепляется на две волны, поляризованные по кругу. Скорости этих волн различны, поэтому при прохождении некоторого расстояния l плоскость поляризации оказывается повернутой на угол, пропорциональный l (эффект Фарадея). Направление вращения определяется относительно оси, совпадающей с Н0, и не

зависит от направления распространения. Фазовая скорость волн зависит от величины постоянного магнитного поля и может сильно различаться.

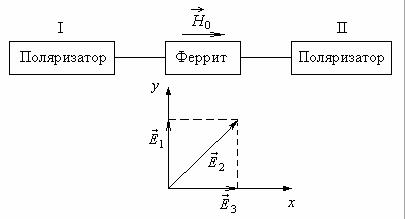
Это свойство феррита используется при конструировании вентильных систем (рис.2).

Рис.2. Схема действия вентильной системы

Пусть поляризатор I создает линейно-поляризованную волну с вектором Е1, направленным по оси y. Пройдя ферритовый образец (циркулятор), волна изменяет положение плоскости поляризации на π/4 (E2). Поляризатор II свободно пропускает волны этой поляризации. Если же волна идет из поляризатора II, то циркулятор повернет плоскость поляризации еще раз на π/4 и вектор E3 будет направлен по оси x.

Чтобы применить к этой задаче формулу (4), необходимо выбрать поверхность интегрирования. Будем считать, что поверхность S состоит из плоской поверхности S1 экрана с отверстием и сферической поверхности S2 с центром в точке М, опирающейся на плоскость S1.

Пусть u(М) и G(М) – комплексные функции координат точки М, имеющие непрерывные первые и вторые частные производные как внутри объема V, так и на поверхности S, ограничивающей объем V. Тогда согласно теореме Грина

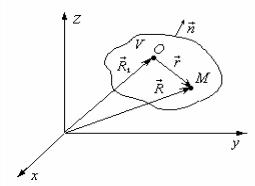
где д/ди означает производную по направлению внешней нормали к объему V

(рис.1).

Пусть функция u является комплексной амплитудой волнового поля и удовлетворяет внутри объема V однородному уравнению Гельмгольца:

которая описывает сферическую волну единичой амплитуды; она называется

функцией точечного источника или функцией Грина для свободного простран-

ства.

Определяя ∆и и ∆G из (2) и (3)

∆u = −k2u; ∆G = −δ(R − R1 )− k2G,

и подставляя в (1), получим

Формула (4) называется интегральной теоремой Кирхгофа-Гельмгольца.

Используем формулу (4) для определения поля волны, прошедшей через экран с отверстием. Волна падает слева на экран; необходимо определить поле в произвольной точке М, расположенной справа от экрана (рис.2).

Чтобы применить к этой задаче формулу (4), необходимо выбрать поверхность интегрирования. Будем считать, что поверхность S состоит из плоской поверхности S1 экрана с отверстием и сферической поверхности S2 с центром в точке М, опирающейся на плоскость S1.

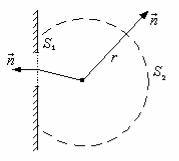
Рис. 2. К задаче дифракции на отверстии

Рассмотрим интеграл по сферической поверхности S2. В этом случае направление внешней нормали совпадает с направлением радиуса

Если радиус сферической поверхности взять очень большим (в пределе можно считать r →∞), то из физических соображений ясно, что интеграл по поверхности S2 должен давать малый вклад в поле точки М. Однако для гармо-

нических полей ( exp(iωt )) обращение интеграла по S2 в нуль происходит

только в том случае, если на функцию u наложить условия, определяющие ее поведение при r →∞.

Потребуем, чтобы

(Ω - телесный угол с вершиной в точке М). Интеграл (1.5) будет стремиться к нулю при r →∞, если функция u будет удовлетворять условию

Условие (6) называется условием излучения Зоммерфельда. Ему удовле-

творяет функция u = exp(-ikr)/r, которая при зависимости от времени в виде exp(iωt) определяет расходящуюся сферическую волну. Так как возмущение, идущее от отверстия в экране, всегда представляет собой комбинацию сферических волн, то условие (6) оказывается выполненным. Интеграл по S2 обращается в нуль, и поле в точке М определяется только значением поля и его производной в отверстии и на теневой стороне экрана.

Однако пока не решена точно соответствующая граничная задача, значения u и дu/дп на S не известны. Поэтому без дополнительных исследований задача может быть решена лишь приближенно при определенных предположениях о значениях u и дu/дп на теневой стороне экрана. Приближенные граничные условия Кирхгофа соответствуют следующим предположениям:

1. Значения u и дu/дп равны нулю всюду, за исключением отверстий.

т.е. или сама функция должна обращаться в нуль на поверхности S, или должна обращаться в нуль ее производная по нормали. Выбор функции Грина G1 обращает в (4) в нуль член, содержащий дu/дп. При этом на поверхности S достаточно знать лишь саму функцию u. Если выбрать вторую функцию Грина G2, то в нуль обращается член, содержащий u, и достаточно на S знать дu/дп. Однако построение функций Грина, удовлетворяющих граничным условиям 1 или 2, известно лишь для задач с достаточно простой геометрией. Вид функций Грина определяется видом поверхности S и свойствами среды и не зависит от положения источника излучения и от поля, создаваемого им на экране. Поэтому можно говорить о функции Грина для полупространства, сферы и т.д.

Угловой спектр плоских волн

Вместо того, чтобы искать решение дифракционной задачи в форме (4), выбрав соответствующим образом функцию Грина, можно использовать метод разложения поля в плоскости экрана по плоским волнам.

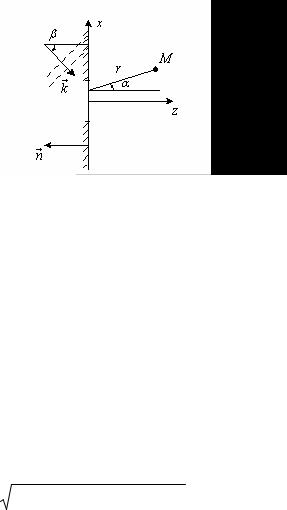
Рассмотрим монохроматическую волну, распространяющуюся в направлении оси z и проходящую через отверстие в непрозрачном экране, расположенном в плоскости z = 0. Комплексная амплитуда в плоскости z = 0 описывается функцией u0(x,y,0). Необходимо определить поле в произвольной точке М(x,y,z) за экраном.

Произведем двумерное Фурье-преобразование функции u0(x,y,0):

Функция F0(kx,ky) называется угловым (пространственным) спектром функции u0(x,y,0). Действительно, подынтегральное выражение в (10) представляет собой комплексную амплитуду плоской гармонической волны в плоскости

дой F0(kx,ky), зависящей от направления распространения (временной множитель exp(iωt) мы всюду опускаем). Вместо переменных kx = k cosα, ky = k cosβ,

kz = k cos γ, где cosα,cosβ,cos γ - направляющие косинусы нормали к фронту

fy = 2kπy = λ−1 cosβ, называемые пространственными частотами. В этих обо-

значениях

Следовательно, выражение (10) представляет разложение комплексной амплитуды волнового поля в плоскости z = 0 в угловой спектр плоских волн.

Если бы угловой спектр был известен в любой плоскости, параллельной экрану, т.е. при любом значении z, то функция u(x,y,z) определялась бы выражением

Поскольку функция u(x,y,z) удовлетворяет уравнению Гельмгольца (среду считаем однородной) (2), то, подставляя (12) в уравнение (2), получим дифференциальное уравнение для функции F(kx,ky,z):

Решая это уравнение при условии F(kx,ky,0) = F0(kx,ky) найдем частное решение, соответствующее волне, распространяющейся в положительном направлении оси z,

Угловой спектр, по мере удаления точки наблюдения от плоскости экрана, изменяется. При kx 2 + ky 2 < k 2 это изменение связано со сдвигом фаз между различными спектральными компонентами (плоскими волнами, распространяющимися под разными углами к оси z). При kx 2 + ky 2 > k 2 выражение (14)

описывает плоские неоднородные волны, амплитуды которых экспоненциально убывают по мере удаления от плоскости z = 0.

В предельном случае, когда kx 2 + ky 2 = k 2 , плоские волны распростра-

няются в направлениях, перпендикулярных оси z и не переносят энергию вдоль оси z.

Лекция № 30. Вычислительные методы в электродинамике

Базирующаяся на уравнениях Максвелла теория электромагнитных явлений представляет собой естественную основу математического моделирования в технике, использующей эти явления. Если учесть быстрый прогресс средств вычислительной техники, не остается сомнений, что в будущем техническое проектирование в высокой степени должно базироваться на строгой теории. К радиоэлектронике это относится в первую очередь, потому что здесь имеется надежная основа в виде системы уравнений Максвелла.

С развитием радиоэлектроники появляется все больше проблем, подход к которым должен быть строго электродинамическим. Отвлечься от существования электромагнитного поля невозможно при проектировании антенн и анализе распространения радиоволн как в природных условиях, так и аппаратуре. По мере того, как в практику входили дециметровые, сантиметровые и еще более короткие волны, принципы построения радиоаппаратуры заметно менялись. Элементы аппаратуры СВЧ существенно неквазистационарны и могут напоминать акустические или оптические устройства в большей степени, чем электротехнические. Особого подхода требуют современные интегральные схемы СВЧ или, например, устройства оптоэлектроники. Но дело не только в принципах построения, а также и в проектировании, которое либо остается в значительной мере эмпирическим, либо должно опираться на неупрощенные математические модели электродинамики.

Центральным является способ представления решения задачи, т.е. электромагнитного поля. Применяя метод разделения переменных (например в задаче о прямоугольном волноводе), мы получаем некоторые формульные выражения векторных функций, которые точно удовлетворяют уравнениям Максвелла и граничным условиям. В таких случаях иногда говорят, что решение получено в замкнутой форме. Хотя в большинстве технически интересных задач это недостижимо, метод разделения переменных оказывается полезным как средство построения систем функций, служащих для представления полей в различных случаях.

Пусть, например, методом разделения переменных получена система решений уравнений Максвелла {En, Hn} (n = 1, 2, …); каждая пара удовлетворяет граничным условиям на некоторой простой границе. В ряде случаев, пользуясь этой системой, можно построить представление решения вида:

(cn – пока неизвестные коэффициенты). Взяв область со сложной границей, можно тем или иным способом (например, в системе точек), подчинить EN и HN требуемым граничным условиям, что при правильном подходе приведет к системе N линейных алгебраических уравнений относительно N коэффициентов cn. Чем выше N, тем лучше удается удовлетворить граничным условиям, если система {En, Hn} обладает нужными свойствами.

Сущность того или иного метода состоит в том, каким путем граничная задача сводится к системе алгебраических уравнений.