Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

lab-mad

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

349.88 Кб

Скачать

☆

<<< < Предыдущая 12 / 22

	y2	y y	2		y y
	1	1	2		1	n
y2 y1		y22			y2 yn		= yy	T	.
	#	#		#	#		= yy		.
	#	#		#	#
		yn y2			2
yn y1		yn y2			yn

Матрица yyT является симметричной, а сумма ее диагональных элементов представляет собой квадрат длины вектора y и всегда положительна для ненулевого y. Следовательно, равен-

ство yT Ry = 0 выполняется только, когда сумма диагональных элементов равна по модулю и

n	n−1 n
противоположна по знаку сумме недиагональных элементов ∑ yi2 + 2∑ ∑ yi y j = 0 .
i=1	i=1 j=i+1

Для случая n = 2 получим: y12 + y22 + 2y1 y2 = 0 . Решив данное квадратное уравнение относительно y1, получим, что yT Ry = 0 при y1 = − y2 .

Признаки Xi представляют собой результаты измерений, где часто число объектов N много больше числа признаков n. Поэтому, в силу возможных ошибок и неточностей измерений, не говоря уже о случайных помехах, линейная зависимость признаков Xi маловероятна. Поэтому, как правило, данная квадратичная форма оказывается строго положительной при любом ненулевом векторе y.

СОБСТВЕННЫЕ ВЕКТОРЫ ЧИСЛА КОРРЕЛЯЦИОННОЙ МАТРИЦЫ

Собственным вектором корреляционной матрицы R, соответствующим собственному числу λ, называется ненулевой вектор x = (x1,... x n )T , удовлетворяющий уравнению Rx = λ x .

Как известно из линейной алгебры, матрица R рассматривается в данном случае как матрица линейного преобразования вектора x в вектор λx. Это означает, что для данного линейного преобразования R в n-мерном пространстве существует такое направление, что преобразование R только растягивает вектор x в λ раз, сохраняя его ориентацию.

Векторное уравнение можно переписать в виде однородного уравнения относительно x: (R − λ E)x = 0 . Данное уравнение имеет ненулевое (нетривиальное) решение только тогда, ко-

гда определитель det(R − λ E) равен нулю. Данный определитель представляет собой уравне-

ние относительно λ и является полиномом n степени вида (−1)n λ n + (−1)n−1 p1λ n−1 +...+ pn = 0 .

Данный полином называется характеристическим полиномом (многочленом), а уравнение det(R − λ E) = 0 - характеристическим уравнением. Характеристическое уравнение имеет n,

вообще говоря, различных корней. При этом его корни λi являются собственными числами преобразования R. В качестве собственных векторов xi, i = 1,... n линейного преобразования R, со-

ответствующих собственным числам λ i, i = 1,... n , берутся векторы единичной длины

∑ xi2j = 1; i = 1,... n , каждый из которых удовлетворяет соответствующему характеристическо-

j=1

му уравнению det(R − λ i E) = 0 . Рассмотрим случай n=2. Тогда получим

1	r12		1	r
R =			=	;
r21		1	r 1

R − λE =	1	− λ r	;	det	(	R − λE	)	=	1	− λ	2 − r2 = 0 .
					(		)		(	)
	r	1− λ

Решением квадратного уравнения λ2 − 2λ +1− r2 = 0 относительно λ являются корни

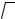
λ1 = 1+ r и λ2 = 1− r .

Отметим следующие свойства собственных чисел.

1) λ 1 > λ 2 > 0 . Так как корреляционная матрица R практически положительно определе-

на, то при произвольном n все ее собственные числа являются действительными и строго положительными λ 1 > λ 2 >... > λ n > 0 .

2)	λ 1 + λ 2 = 2 . Вычислим след	матрицы R как сумму ее диагональных элементов
trR = r11 + r22 = 1+1 = 2 . Следовательно,		trR = λ 1 + λ 2 , то есть сумма собственных чисел корре-
		n
ляционной матрицы равна ее следу. При произвольном n получим ∑λ i = trR .
		i=1
3)	λ 1λ 2 = 1− r2 . Определитель корреляционной матрицы равен det R = 1− r2 . Следова-

тельно, det R = λ 1λ 2 . При произвольном n получим ∏λ i = (−1)n det R = det R . Следовательно,

i=1

произведение собственных чисел равно определителю корреляционной матрицы, взятому со знаком плюс, так как все собственные числа положительны.

Найдем собственные векторы x1 и x2, соответствующие собственным числам λ1 и λ2. Из характеристического уравнения следует, что первый вектор найдется из уравнения

1	− λ 1	r x11	−r	r x11		0
	1		=		=	.
r	1	− λ 1 x12	r	− r x12	0

Согласно определению x112 + x122 = 1 . Тогда получим систему уравнений

−rx11 + rx12			= 0
	rx11	− rx12	= 0

	2	2	= 1.
	x11	+ x12

Из решения данной системы следует, что x11 = x12 = ± 2 / 2 = ±0.707 . Два решения указы-

вают на противоположные направления вдоль диагонали первого и третьего квадрантов плоскости координат:

x11	= 0.707	x11	= −0.707
	= 0.707		= −0.707 .
x12	= 0.707	x12	= −0.707 .

Второй вектор найдется из уравнения

1− λ		2	r x21			r r x21				0
	r 1		− λ		x	=	r r	x	=	0	.
				2
					22			22

В результате получим два решения, указывающие на противоположные направления вдоль диагонали второго и четвертого квадрантов плоскости координат

x21 = 0.707 x21 = −0.707x22 = −0.707 x22 = 0.707 .

Как сразу нетрудно заметить, собственные векторы матрицы R, то есть вещественной симметричной матрицы, соответствующие различным собственным числам, ортогональны между собой. Покажем это для произвольного n. Раccмотрим уравнения

Rx1 = λ 1x1 и Rx2 = λ 2x2 , где λ 1 ≠ λ 2 . Домножим каждое из уравнений на собственный

вектор другого уравнения и получим xT Rx	1	= λ	xT x		1	и	xT Rx	2	= λ	2	xT x	2	. Так как
2	1		1	2	1		1	2		2	1	2
xT2 Rx1 = x1T (xT2 R)T = x1T RT x2 = x1T Rx2 ,
то, вычтя одно уравнение из другого, получим
0 = λ 1xT2 x1 − λ 2x1T x2 = λ 1xT2 x1 − λ 2xT2 x1 = (λ 1 − λ 2 )xT2 x1 .
Отсюда следует, что xT2 x1 = 0 . Следовательно,						собственные					векторы линейного

преобразования R образуют ортонормированный базис в n-мерном пространстве. Такие векторы называются главными компонентами корреляционной матрицы.

Главные компоненты корреляционной матрицы обладают весьма важными свойствами, которые имеют содержательный смысл в обработке данных и поэтому широко используются. Ниже мы покажем геометрический смысл главных компонент на плоскости.

ПРИВЕДЕНИЕ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ К ДИАГОНАЛЬНОЙ ФОРМЕ

Преобразование корреляционной матрицы к диагональной форме основано на следующем свойстве вещественной (действительной) симметричной матрицы. Пусть R - невырожденная корреляционная матрица и имеет n различных собственных чисел λ i , i = 1,... n . Пусть

ai, i = 1,... n - соответствующие собственные векторы, выбранные из пар собственных векторов, соответствующих каждому собственному числу, составляющие ортонормированный базис в n- мерном пространстве. Пусть A = (a1,... an ) - матрица, столбцами которой являются собственные векторы ai. Рассмотрим матрицу

aT			aT a			... aT a		1	... 0
	1	(a1		1	1	1	n			= E,
AT A =	#	(a1	... an ) =	#		#		=		= E,
	T			T		T
an			an a1			... an an		0	... 1

где E - единичная матрица. Следовательно, матрица A является ортогональной.

Напомним, что некоторая матрица A ортогональна, если A−1A = AT A = E . По уравнению Ra = λ a получим RA = (λ1 a1 ... λ nan ) , где столбцами матрицы в правой части являются векто-

ры λ iai . Учитывая, что векторы ai ортогональны, получим

λ aT a

... λ

aT a

... 0

(λ 1a1

1 1 1

AT RA =

... λ nan ) =

= Λ .

λ 1an a1

... λ nan an

λ n

Матрица AT RA диагональна, и ее диагональные элементы являются собственными числами. Из условия AT RA = Λ следует AAT RAAT = AΛAT и R = AΛAT , так как AAT = AT A = E . Следовательно, невырожденная корреляционная матрица R может быть приведена к диагональной форме путем ортогонального преобразования AT RA .

Пусть x = (x1,... x n )T - некоторый вектор, заданный своими проекциями на осях координат

X i, i = 1,... n . Рассмотрим вектор y = (y1,... yn )T , где y = AT x , а строками матрицы AT являются собственные векторы aiT линейного преобразования R. Тогда

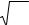
					n
	y	aT x			∑a1 j x j
	1		1	j=1		#
y =	#	=	#	=		#			.
			T		n	a		x
yn		an x			∑	a	nj	x
					∑		nj		j
					j=1

Следовательно, компонента yi вектора y - это скалярное произведение собственного вектора ai и вектора x. С другой стороны, скалярное произведение - это произведение модулей

векторов ai и x на косинус угла между ними. Так как ai = 1, то это есть произведение x на

косинус угла между ai и x - проекция вектора x на ai. Поэтому вектор y представлен своими проекциями на ортонормированный базис собственных векторов корреляционной матрицы R. Можно считать, что новый базис ai, i = 1,... n образует новое n-мерное пространство признаков

Yi = (y1,... yN )T , i = 1,... n , принимающих свои значения на N объектах.

Значения n признаков Yi, как бы измеренных на N объектах, образуют новую матрицу данных Y = XA , полученную из матрицы X ортогональным преобразованием A:

yT		xT a		1
	1		1	1
Y =	#	=	#
	T		T
yN		xN a1

xT a		xT
1	n		1	(a1	an ) = XA .
#		=	#	(a1	an ) = XA .
T			T
xN an		xN

Корреляционная матрица R, вычисленная по матрице X, представляет собой мат-

рицу

X T

R =

( X1

Xn ) =

XT X .

Вычислим среднее признака Yj

y j

∑xTi a j =

∑∑ xik akj =

∑akj ∑ xik =∑akj x k =0 ,

i=1

i=1 k =1

N k =1

i=1

k =1

так как матрица X стандартизована. Вычислим величину

YT Y =

(XA)T

(XA) =

AT XT XA = AT RA = Λ =

λ n

Тогда матрица Λ является ковариационной матрицей, вычисленной по матрице Y. Диагональная структура матрицы Λ показывает, как и следовало ожидать, независимость признаков Yi, i = 1,... n . Собственные числа λi являются дисперсиями этих призна-

ков, то есть λ i = σ 2i . Если разделить значения компонент каждого признака Yi на вели-

чину σ i = λ i ,					то матрица Y будет приведена к стандартизованному виду. Тогда пре-
образование			Y = XAΛ−1/2 даст стандартизованную матрицу данных Y с единичной кор-
реляционной матрицей:
1			1			T	1
		YT Y	=			(XAΛ−1/2 ) (XAΛ−1/2 ) =		Λ−1/2AT XT XAΛ−1/2 =
	N			N			N

= Λ−1/2AT RAΛ−1/2 = Λ−1/2ΛΛ−1/2 = Λ1/2Λ−1/2 = E .

ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЧИСЕЛ И ВЕКТОРОВ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ

В задачах обработки часто возникает необходимость в определении собственных векторов корреляционной матрицы, соответствующих тем или иным собственным числам. Как было показано, для нахождения собственных чисел и векторов следует найти корни характеристического полинома порядка n относительно λ. Затем для каждого λ i, i = 1,... n следует найти свой соб-

ственный вектор, который мы обозначим как ai = (a1i,... ani )T , как решение однородной системы

линейных уравнений относительно этого собственного вектора при ограничении на его длину

ai = ∑a2ji = 1. j=1

Известно, что точные методы поиска корней полинома и корней системы линейных уравнений представляют собой громоздкие процедуры при больших n, практически начиная с n ≥ 3 . Поэтому данная задача часто решается итерационными методами вычислительной математики. Итерационные методы для одновременного поиска всех собственных чисел и векторов представляют собой методы преобразования симметричной матрицы в диагональную форму. Часто требуется вычислить только максимальное собственное число и соответствующий ему собственный вектор. Рассмотрим известный итерационный метод приближенного вычисления максимального собственного числа и соответствующего собственного вектора.

Пусть все	собственные числа различны и упорядочены λ 1 > λ 2 >... > λ n > 0 . Пусть
x = (x1,... x n )T -	некоторый вектор. Совокупность собственных векторов ai, i = 1,... n корреля-

ционной матрицы R образует ортонормированный базис, в пространстве которого вектор x преобразуется в вектор y = AT x . Т.к. матрица А ортогональна, то y = A−1x и x = Ay , где вектор х представлен своим разложением по базису собственных векторов:

= y1a1 + ... + ynan

= ∑ yiai .

x = (a1,... an ) #

i=1

Тогда

Rx = R

∑ yiai

∑ yi Rai = ∑ yiλiai .

i=1

Выделим первое слагаемое

Rx = y λ a

= λ

y a

1 1 1

∑ i

1 1 1

∑ i

λ1

i=2

Умножим это равенство еще раз слева на R:

RRx = R2x = Rλ

y a +

y Ra

1 1

∑ i

λ1

∑ i

i=2

λ1 y1λ1a1

+ ∑ yi

ai = λ12 y1a1 + ∑ yi

i=2

λ	i
	i	Rai	=
		Rai	=
λ1
λ1

Тогда для некоторого s получим
	n	λ	i	s
Rs x = λ1s y1a1 + ∑ yi			i		ai	.
Rs x = λ1s y1a1 + ∑ yi		λ			ai	.
	i=2	λ	1
			1

и lim Rs x = λ1s y1a1 .

Так как λ 1 > λ 2 >... > λ n

> 0

и 0 ≤

< 1, то

lim

= 0

λ 1

λ1

s→∞

Тогда при y1 ≠ 0 первый собственный вектор определяется достаточно далеким членом

последовательности x, Rx, R2x, ...Rs x, ... .

Но при

> 1

получим, что

lim λ s y a = ∞ ,

а при

s→∞

< 1 получим, что lim λ s y a = 0 .

Следовательно, вектор Rs x стремится по направлению к

s→∞

вектору a1, но его длина значительно отличается от единичной.

Поэтому строят

две

другие

последовательности

x0 , x1,... xs , ...

z1, ... zs, ...

, где

= Rxs−1, xs = zs / || zs

|| ,

начиная с некоторого вектора x0

единичной длины.

Следовательно,

|| xs ||= 1 при любом s,

а предел последовательности {xs } стремится по направлению к вектору

a1. Следовательно, lim xs

= a1 . Тогда zs+1 = Rxs ≈ λ1a1

zs+1 = λ 1a1 = λ 1

∑ai21 = λ 1 .

s→∞

i=1

Задание на работу

Ознакомиться с теоретической справкой к данной лабораторной работе. Найти собственные векторы и собственный числа корреляционной матрицы.

Содержание отчета

Номер и название лабораторной работы; Цель лабораторной работы; Пояснительная записка к проекту; Выводы.

Контрольные вопросы

1.Основные свойства корреляционной матрицы

2.Собственные векторы и собственный числа квадратной матрицы

3.Интерпретация главных компонент на плоскости

4.Алгоритм приближенного вычисления максимального собственного числа

Лабораторная работа №3

ВИЗУАЛИЗАЦИЯ ДАННЫХ В ПРОСТРАНСТВЕ ГЛАВНЫХ КОМПОНЕНТ

Цель и задача работы

2D и 3D представление данных в пространстве первых главных компонент

Теоретические положения

ПРЕДСТАВЛЕНИЕ ГЛАВНЫХ КОМПОНЕНТ НА ПЛОСКОСТИ

Пусть в соответствии со статистической гипотезой порождения матрицы данных X в n- мерном пространстве признаков существует многомерное нормальное распределение с плотно-

стью вероятности f (x / µ, Σ ) . Для стандартизованной матрицы X мы полагаем, что

f (x / 0, R) =	1		−	1	x	T	R	−1
f (x / 0, R) =	(2π)n det R	exp	−		x		R	x .
	(2π)n det R			2

Проведем ортогональное преобразование матрицы данных X в новую матрицу данных Y = XA , где A - матрица, столбцами которой являются собственные векторы корреляционной матрицы R. Тем самым мы перешли в новое признаковое пространство, образованное ортонормированным базисом линейного преобразования R. Очевидно, что в новом признаковом пространстве задано нормальное распределение с плотностью вероятности

f (y / 0, Λ ) =	1		−	1	y	T	−1
f (y / 0, Λ ) =	(2π)n det Λ	exp	−		y		Λ y .
	(2π)n det Λ			2

Так как Λ = AT RA,		то	Λ−1 = (AT RA)−1 = A−1R−1(AT )−1 = AT R−1A ,
							1		0
	λ 1	0
								λ 1
				n				λ 1
det Λ = det				= ∏λ i ;	Λ−1	=			1		.
				i=1					1
	0	λ n					0
	0	λ n					0
										λ n

Тогда f (y / 0, Λ ) =	1
Тогда f (y / 0, Λ ) =	n
	(2π)n ∏
	i=1

		1	n	y2
	−		∑	i
exp	−			i	.
		2 i=1 λ i
λ i

Пусть n = 2, тогда двухмерное нормальное распределение имеет вид

f (y / 0, Λ ) = 2π λ λ

exp −

+ λ

Рассмотрим уравнение

= p,

p > 0 . Из курса аналитической геометрии из-

λ2

λ 1

вестно,

что это уравнение

линии

второго порядка. При заданном p и найденных

λ 1 и λ 2

данная линия является линией постоянного значения плотности вероятности

− p / 2

Преобразуем данное уравнение линии второго порядка к канониче-

2π

λ λ

скому виду

= 1. Так как λ 1 > λ 2 > 0 , то данное уравнение является канониче-

pλ 1

pλ2

ским уравнением эллипса в системе координат, образованной собственными векторами,

которые соответствуют собственным числам

λ 1 и λ 2 .

Если r>0, то λ 1 = 1+ r и λ 2 = 1− r и система главных компонент y10y2

повернута на 450

относительно исходной системы координат x10x2. Если r<0, то λ 1 = 1− r и λ 2 = 1+ r

и система

главных компонент y10y2 повернута на 1350 относительно x10x2. Если r=0, то λ 1 = λ 2 = 1. Тогда

уравнение эллипса представляет собой уравнение окружности y2

+ y2 = p

радиуса

p . В этом

случае система главных компонент y10y2

может быть ориентирована в любом направлении, то

есть любое направление

является главным для такого линейного преобразования R. Если r=1,

то λ 1 = 2, λ 2 = 0 .

Тогда уравнение эллипса для линии постоянного значения плотности вероят-

ности

вырождается

уравнение

для

двух

точек,

расположенных

на

оси

0y1,

вида

y = ±

p 1+ r

)

= ±

2 p,

= 0 (Рис. 2.1).

(

p(1 + r )

p 1 − r

)

(

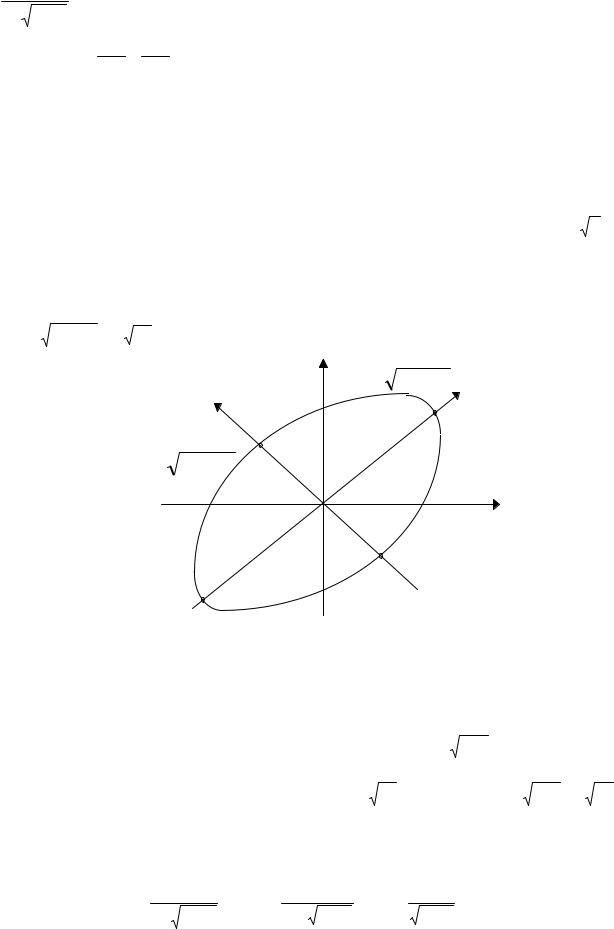
Рис.2.1. Главные компоненты

Определим уравнение максимального эллипса в соответствии с правилом “трех сигм”, согласно которому 99.73% всех наблюдений сосредоточено внутри него. Согласно свойствам канонического уравнения эллипса его главная ось совпадает с направлением первой главной

компоненты 0y1. Длина главной полуоси составляет величину pλ 1 . В то же время максимальное положительное случайное отклонение величины y1 на оси 0y1 от центра координат с вероятностью 0.9973 не превышает величины 3σ 1 = 3 λ 1 . Следовательно, pλ 1 = 3 λ 1 , откуда p=9. Проведя те же рассуждения для второй оси максимального эллипса, получим, что урав-

	y2		y2
нение имеет вид	1	+	2	= 1 и описывает линию постоянного значения плотности вероятно-
нение имеет вид	9λ 1	+	9λ 2
	9λ 1		9λ 2
сти на уровне f ( p) =			1	e− p / 2 ≈	1	e−4.5 = 0.004 .
		2π λ 1λ 2			6.28 1− r2	1− r2

Так как длина главной полуоси равна	pλ	1	=	(	+ r	)	, то при увеличении значения r
				p 1

длина главной полуоси увеличивается. В то же время длина второй полуоси эллипса pλ2 = p(1− r) уменьшается при увеличении r. Следовательно, чем сильнее связаны призна-

ки X1 и X2 корреляционной зависимостью, тем больше дисперсия σ 12 = λ 1 признака Y1 и меньше дисперсия σ 22 = λ 2 признака Y2 при неизменной суммарной дисперсии σ 12 + σ 22 = λ 1 + λ 2 = 2 .

МОДЕЛЬ ГЛАВНЫХ КОМПОНЕНТ

Пусть новая матрица данных получена путем ортогонального преобразования

Y = XAΛ−1/2 . Такая матрица является стандартизованной, то есть N1 YT Y = E . Тогда преобразо-

вание некоторого вектора x к вектору y выполняется как yT = xT AΛ−1/2 или y = Λ−1/2AT x . Вы-

полним обратное преобразование X = YΛ1/2AT . Тем самым мы выразили матрицу исходных данных через матрицу Y.

Согласно гипотезе скрытых факторов, значение каждого исходного признака, измеренного на некотором объекте, зависит от влияния некоторых “скрытых” неизмеряемых факторов и определяется совокупностью их вкладов, пропорциональных силе влияния. Тогда матрицу Y

будем считать матрицей n скрытых факторов, а матрицу UT = Λ1/2AT - матрицей факторных нагрузок. Тогда каждая компонента некоторого вектора x, измеренного на некотором объекте,

представляется как совокупность значений факторов на этом объекте xT = yT Λ1/2AT или

x = AΛ1/2y = Uy :

∑

λ i a1i yi

i=1

λ 1a1

= (

λ n an )

= ∑ yi λ i ai =

i=1

∑

λ i an i yi

i=1

Тогда корреляционная матрица имеет вид

R =

XT X =

(YΛ1/2AT )

(YΛ1/2AT ) =

AΛ1/2YT YΛ1/2AT =

= (AΛ1/2 )(Λ1/2AT ) = UUT = AΛAT .

Рассмотрим взаимные корреляции между признаками из X и факторами из матри-

цы Y

N1 XT Y = N1 (YΛ1/2AT )T Y = N1 AΛ1/2YT Y = AΛ1/2 = U .

Следовательно, матрица U факторных нагрузок является матрицей взаимных корреляций между исходными признаками и скрытыми факторами, где элемент uij = aij λ i равен величине

взаимной корреляции между признаком Xi и фактором Yj. Рассмотрим структуру корреляционной матрицы

		n	n
		∑λ ia12i	∑λ ia1iani
R = UUT =		i=1	i=1	#
R = UUT =		#		#	.
		n		n
		∑λ iania1i		2
		∑λ iania1i		∑λ iani
	i=1			i=1
			n	n
Дисперсия σ 2k = rkk			= ∑λ iaki2 = ∑uki2 = 1 некоторого признака Xk есть величина, со-
			i=1	i=1

стоящая из вкладов соответствующих главных компонент. Полный вклад всех главных компонент в дисперсии всех признаков составляет величину

n	n	n	= trUUT = trR = trΛ = n .
∑	σ 2k = ∑	∑λ iaki2	= trUUT = trR = trΛ = n .
k =1	k =1	i=1

При преобразовании к главным компонентам вместо n исходных признаков получается такое же число факторов. Но вклад довольно большой части главных компонент в суммарную дисперсию признаков является небольшим. Поэтому часто целесообразно исключить те главные компоненты, вклад которых невелик. При этом оказывается, что при помощи m первых наиболее весомых главных компонент, где m<n, можно объяснить основную долю суммарной дисперсии признаков. Эта доля называется объясняе-

m	m
мой долей дисперсии h2 = ∑σ 2i	= ∑λ i < n , где обычно h2 / n ≥ 0.8 .
i=1	i=1
	Задание на работу

Выполнить проекцию объектов на первые два и первые три собственных вектора, отобразить полученные векторы на плоскости (2D) и в ортогональной проекции трех координат (3D).

Содержание отчета

Номер и название лабораторной работы; Цель лабораторной работы; Пояснительная записка к проекту; Выводы.

Контрольные вопросы

1.Основные свойства корреляционной матрицы

2.Собственные векторы и собственный числа квадратной матрицы

3.Интерпретация главных компонент на плоскости

4.Алгоритм приближенного вычисления максимального собственного числа

5.Методы визуализации данных

6.Задача Карунена-Лоэва

<<< < Предыдущая 12 / 22

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.05.2019131.58 Кб5L7.doc
#
11.08.2019129.02 Кб2L8.doc
#
05.05.20192.53 Mб1L9.doc
#
17.04.2019504.32 Кб3lab-26т.doc
#
16.03.2016213.5 Кб15Lab-3.doc
#
10.05.2015349.88 Кб6lab-mad.pdf
#
10.05.20152.52 Mб65lab-part1.doc
#
16.03.2016951.4 Кб27lab-part1.pdfФизика.pdf
#
17.12.20181.57 Mб29lab-part2.doc
#
10.05.2015208.9 Кб37Lab01wd1.doc
#
10.05.2015499.33 Кб9lab1.pdf