
Число дискретных собственных значений спектральной задачи Шредингера на всей прямой
Сформулируем
и докажем некоторые леммы и теоремы о
числе N
дискретных собственных значений
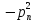 спектральной задачи Шредингера,
описываемой уравнением
спектральной задачи Шредингера,
описываемой уравнением
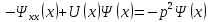 -∞<
-∞<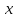 <+∞
(1)
<+∞
(1)
Мы
всюду предполагаем, что функция
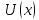 действительна и регулярна при всех
действительных значениях
действительна и регулярна при всех
действительных значениях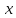 и стремится к нулю при
и стремится к нулю при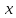 →±∞;во
многих случаях удобно предположить
даже, что функция
→±∞;во
многих случаях удобно предположить
даже, что функция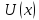 имеет компактный носитель, т.е тождественно
равна нулю при достаточно больших
действительных значениях
имеет компактный носитель, т.е тождественно
равна нулю при достаточно больших
действительных значениях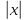 ,скажем
при
,скажем
при ,
хотя окончательные результаты справедливы
и в более общем случае. Хорошо известно,
что все собственные значения не вырождены
и величина
,
хотя окончательные результаты справедливы
и в более общем случае. Хорошо известно,
что все собственные значения не вырождены
и величина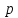 должна быть действительной; мы будем
считать, что
должна быть действительной; мы будем
считать, что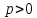 .
.
Лемма 1.
Число
дискретных собственных значений
уравнения(1) равно числу действительных
нулей
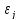 функции
функции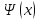 , определяемой уравнением
, определяемой уравнением
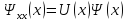 (2)
(2)
с граничными условиями
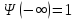 ,
,
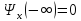 (3)
(3)
а именно оно равно N:
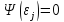 ,
,
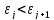 j=1,2,……,
N (4)
j=1,2,……,
N (4)
Доказательство.
Эту
лемму можно доказать, заметив, что
вычислить и тем самым посчитать
дискретные собственные значения можно,
следуя за нулями
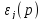 решения
решения
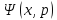 уравнения (1) с граничным условием
уравнения (1) с граничным условием
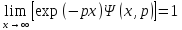 (5)
(5)
При
возрастающих значениях
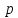 ,начиная с
,начиная с
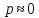 ,с
учетом того,что каждое значение
,с
учетом того,что каждое значение
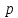 ,при котором число этих нулей уменьшается
на единицу(вследствие выхода на
бесконечность самого правого
нуля),соответствует одному дискретному
собственному значению.
,при котором число этих нулей уменьшается
на единицу(вследствие выхода на
бесконечность самого правого
нуля),соответствует одному дискретному
собственному значению.
Замечание.
Здесь
и далее мы для простоты исключаем из
рассмотрения крайний случай, когда
функция
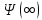 конечна ,соответствующий в некотором
смысле наличию дискретного собственного
значения при
конечна ,соответствующий в некотором
смысле наличию дискретного собственного
значения при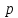 =0.Этим
объясняется то, что некоторые из
приводимых ниже результатов оказываются
в противоречии с тривиальным случаем
=0.Этим
объясняется то, что некоторые из
приводимых ниже результатов оказываются
в противоречии с тривиальным случаем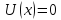 ,
означающим,чтоN=0.
,
означающим,чтоN=0.
Лемма 2.
Определим
функцию
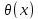 нелинейным дифференциальным уравнением
первого порядка
нелинейным дифференциальным уравнением
первого порядка
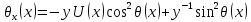 (6)
(6)
C граничным условием
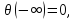 (7)
(7)
Причем у –произвольная постоянная. Тогда число дискретных собственных значений N дается формулой
 (8)
(8)
Доказательство
Положим
 (9)
(9)
Тогда из уравнения (2) и условия (3) следует уравнение (6) с условием (7).Кроме того ,из условия (4),очевидно ,следует, что
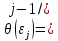 2)π
(10)
2)π
(10)
Заметим,
что упорядочение значений
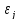 ,даваемое
формулой (4),согласуется равенством
(10),как следует из соотношения
,даваемое
формулой (4),согласуется равенством
(10),как следует из соотношения
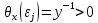 (11)
(11)
Наконец,
из уравнения (9) ясно, что асимптотическое
значение
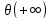 должно с целым кратным числа π,а это
вместе с соотношениями (10) и (4) означает
справедливость формулы (8),что и требовалось
доказать.
должно с целым кратным числа π,а это
вместе с соотношениями (10) и (4) означает
справедливость формулы (8),что и требовалось
доказать.
Лемма 3.
Определим функцию µ(x) нелинейным дифференциальным уравнением первого порядка
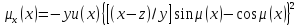 (12)
(12)
и граничным условием
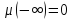 (13)
(13)
Где
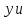
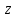 -произвольные
постоянные(но
-произвольные
постоянные(но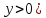 .Тогда
число дискретных собственных значений
.Тогда
число дискретных собственных значений дается формулой
дается формулой
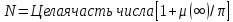 (14)
(14)
(при
условии, что правая часть положительна
;в противном случае
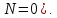
Доказательство
Положим
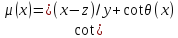 (15)
(15)
Тогда
уравнение (12) немедленно следует из
уравнения (6),а условие (13) легко получить
из условия (7).Чтобы доказать формулу
(14),введем для удобства координаты
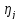 в которых обращается в нуль производная
в которых обращается в нуль производная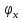 ,а не сама функция
,а не сама функция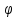 .Тогда
.Тогда
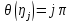 (16)
(16)
и ,очевидно, из соотношений (10) и (11) следует ,что
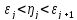 (17)
(17)
Заметим,
что если функция
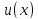 меняет знак, при каждом значенииj
может быть более одного значения
меняет знак, при каждом значенииj
может быть более одного значения
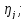 в таком случае число последних должно
быть нечетным и проводимые рассуждения
относятся к крайним правым из них.В то
же время из соотношения (15) следует, что
в таком случае число последних должно
быть нечетным и проводимые рассуждения
относятся к крайним правым из них.В то
же время из соотношения (15) следует, что
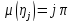 ,
,
 (18)
(18)
Предположим
теперь ,что
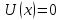 при
при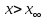 и что
и что
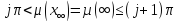
Поскольку
знак функции
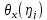 тот же ,что и у функции
тот же ,что и у функции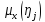 ,это
означает, что
,это
означает, что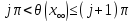 ,и поэтому формула (6) выполняет соотношение
,и поэтому формула (6) выполняет соотношение
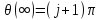 ,
чем наряду с формулой (8) и завершает
доказательство.
,
чем наряду с формулой (8) и завершает
доказательство.
Лемма 4.
Пусть
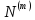 -число дискретных собственных
значений,связанных в силу уравнения
(1) с функцией
-число дискретных собственных
значений,связанных в силу уравнения
(1) с функцией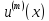 ,m=1,2,
и предположим, что
,m=1,2,
и предположим, что
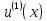 ≤
≤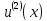 ,
-∞<x<∞
(19)
,
-∞<x<∞
(19)
Тогда
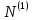 ≥
≥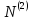 (20)
(20)
Перейдем
теперь к доказательству теоремы о нижней
границе числа
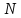 дискретных собственных значений. Оценки
других границ можно получить используя
приведенные выше результаты
дискретных собственных значений. Оценки
других границ можно получить используя
приведенные выше результаты
Теорема 1(о нижней границе).
Число
 уравнения (1) ограничено снизу выражением
уравнения (1) ограничено снизу выражением
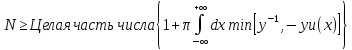 ,
(21)
,
(21)
Где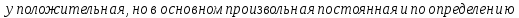
Min(a,b)=a if a≤b (22a)
Min(a,b)=b if a≥b (22б)
Доказательство.
Пусть
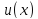 при
при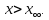 Тогда из уравнения (6) следует,что если
Тогда из уравнения (6) следует,что если
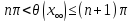 ,то
,то
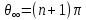 .Отсюда
из формулы (8) следует формула
.Отсюда
из формулы (8) следует формула
 (23)
(23)
(мы
игнорируем крайний случай, когда функция
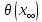 равна целому кратному числу
равна целому кратному числу .
В то же время из уравнения (6) следует,
что
.
В то же время из уравнения (6) следует,
что
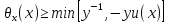 (24)
(24)
Так
как минимальное значение выражения
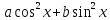 по всем действительным значениям
по всем действительным значениям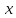 есть
есть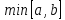 и это вместе с формулой (7) дает
и это вместе с формулой (7) дает
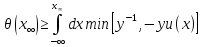 (25a)
(25a)
Или,что
эквивалентно(так как при положительном
значении
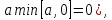
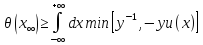 (25б)
(25б)
Эта формула вместе с формулой (23) дает неравенство (21),что и требовалось доказать.
Следствие 1.1
Если
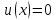 при -∞<x<∞,то
при -∞<x<∞,то
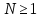 .
.
Доказательство.
Это тривиальным образом следует из формулы (21).
Следствие 1.2
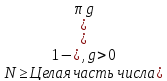 (26)
(26)
При условии, что
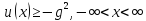 (27)
(27)
Доказательство
Это
следует из формулы (21),если
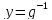 .
.
Теперь
найдем верхние границы числа
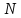 дискретных собственных значений,
связанных с функцией
дискретных собственных значений,
связанных с функцией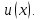 При этом удобнее будет устанавливать
также границы для неположительного
потенциала
При этом удобнее будет устанавливать
также границы для неположительного
потенциала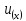 ,связанного
с потенциалом
,связанного
с потенциалом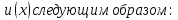
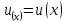 при
при
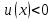 (28а)
(28а)
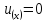 при
при
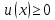 (28б)
(28б)
Тогда
в силу леммы 4 такие границы тем более
будут справедливы для
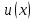 .
.
Эти границы удобно выразить через интегралы
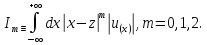 (29)
(29)
В данной формуле и всюду ниже z-произвольная(действительная)постоянная.
Теорема 2(о верхней границе)
Верхняя
граница числа
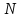 дискретных собственных значений
уравнения (1) дается выражением
дискретных собственных значений
уравнения (1) дается выражением
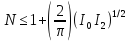 (30)
(30)
Доказательство.
Формулу
(12) можно переписать(с заменой
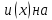
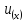 )в виде
)в виде
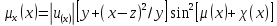 (31)
(31)
где
 (32)
(32)
Из формул (13),(29),и (31) немедленно следует
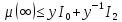 (33)
(33)
При
оптимальном выборе
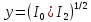 с учетом формулы (14) мы получаем соотношение
(30),что и требовалось доказать.
с учетом формулы (14) мы получаем соотношение
(30),что и требовалось доказать.
Теорема 3.(о верхней границе по Баргману)
Число
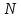 дискретных собственных значений
уравнения (1) ограничено сверху выражением
дискретных собственных значений
уравнения (1) ограничено сверху выражением
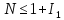 (34)
(34)
Доказательство.
Рассмотрим
функцию
 , определенную формулами (31) и (13);очевидно,
что это неубывающая функция переменной
, определенную формулами (31) и (13);очевидно,
что это неубывающая функция переменной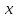 .Определим положения
.Определим положения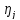
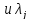 формулами
формулами
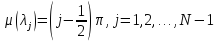 (35а)
(35а)
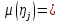
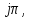
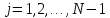 (35б)
(35б)
Эти формулы согласуются с формулой (14).Справедливо правило упорядочения
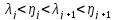 (36)
(36)
Определим
теперь функцию
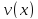 ,положив
,положив
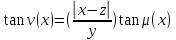 (37)
(37)
Тогда уравнение (31) даёт
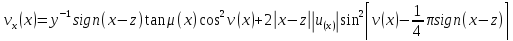 (38)
(38)
А из формул (13) и (35) следуют равенства
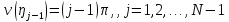 (39a)
(39a)
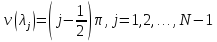 (39б)
(39б)
Причем мы принимаем
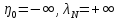 (40)
(40)
Для
удобства определим 2N+1
величин
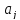 и
и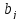 следующим образом
следующим образом
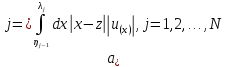 (41a)
(41a)
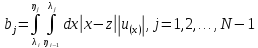 (41б)
(41б)
Тогда, очевидно
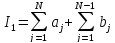 (42)
(42)
Причем
эта формула соответствует разбиению
интервала интегрирования
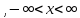 в формуле (29) на 2N+1
интервалов от
в формуле (29) на 2N+1
интервалов от
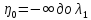 ,от
,от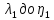 ,от
,от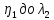 и т.д. и наконец, от
и т.д. и наконец, от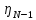 до
до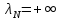 .
.
Теперь докажем, что
Если
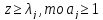 (43а)
(43а)
Если
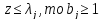 (43б)
(43б)
Из
этих неравенств следует, что, каково бы
ни было значение
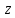 ,в сумме 2N-1
,в сумме 2N-1
Положительных членов в формуле (42) по крайней мере N-1 членов не меньше единицы ,а отсюда следует неравенство (34), которое нам и требуется доказать.
Остается
доказать неравенства (43).Сначала
рассмотрим случай
 Тогда при
Тогда при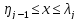 из формул (38) и (35) следует ,что
из формул (38) и (35) следует ,что
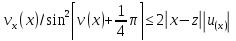 (44a)
(44a)
Интегрирование
от
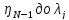 дает (в силу соотношений(39)
дает (в силу соотношений(39)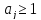 ,и тем самым неравенство (43а) доказано.
Рассмотрим случай
,и тем самым неравенство (43а) доказано.
Рассмотрим случай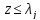 .Тогда
при
.Тогда
при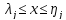 из формул (38) и (35) следует
из формул (38) и (35) следует
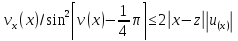 (44б)
(44б)
Интегрирование
от
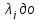
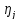 дает теперь в силу соотношений (39)
дает теперь в силу соотношений (39)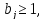 а тем самым доказано и неравенство
(43б).
а тем самым доказано и неравенство
(43б).
Заметим, что из формулы (34) и очевидного неравенства
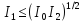 (45)
(45)
Следует
неравенство, аналогичное неравенству
(30),но менее строгое(так как
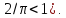
Легко
видеть, что верхняя и нижняя границы
теорем 1-3 суть наилучшие возможные;
действительно ,существуют специальные
функции
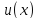 ,их «насыщающие».Для границы теоремы 1
и произвольного числаN
«насыщающей» функцией является
прямоугольная яма
,их «насыщающие».Для границы теоремы 1
и произвольного числаN
«насыщающей» функцией является
прямоугольная яма
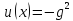 при
при при
при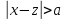 ,где
,где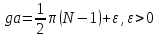 ;для
границ теорем 1-3 приN=1
насыщающей является функция
;для
границ теорем 1-3 приN=1
насыщающей является функция

1Все наши дальнейшие рассуждения легко распространяются и на тот случай, когда V имеет конечное число особых точек такого же рода, как начало координат в рассматриваемом случае.
