2.Рациональные уравнения
.doc
§2.
РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
1)
Квадратные уравнения.
![]() ,
,
![]() .
(1)
Функция
.
(1)
Функция
![]() ,
где
,
где
![]() ,
называется квадратичной функцией.
График этой функции – парабола, координаты
вершины которой равны:
,
называется квадратичной функцией.
График этой функции – парабола, координаты
вершины которой равны:
![]() .
При
.
При
![]() ветви параболы направлены вверх, а при
ветви параболы направлены вверх, а при
![]() – вниз.
– вниз.
![]() – дискриминант квадратного уравнения
(1).
При
– дискриминант квадратного уравнения
(1).
При
![]() уравнение (1) имеет два корня:
уравнение (1) имеет два корня:
![]() ,
,
![]() ;
при
;
при
![]() –
один корень (два равных корня)
–
один корень (два равных корня)
![]() ,
а при
,
а при
![]() уравнение (1) корней не имеет.
Приведенное квадратное уравнение:
уравнение (1) корней не имеет.
Приведенное квадратное уравнение:
![]() .
(2)
Теорема
Виета.
Если квадратное уравнение (2) имеет корни
.
(2)
Теорема
Виета.
Если квадратное уравнение (2) имеет корни
![]() и
и
![]() ,
то
,
то
![]() .
Обратная
теорема.
Если числа
.
Обратная
теорема.
Если числа
![]() и
и
![]() таковы, что
таковы, что
![]()
![]() ,
то они являются
корнями квадратного уравнения
,
то они являются
корнями квадратного уравнения
![]() .
Разложение
квадратного трехчлена на линейные
множители:
если
.
Разложение
квадратного трехчлена на линейные
множители:
если
![]() и
и
![]() корни квадратного уравнения (1), то
корни квадратного уравнения (1), то
![]() .
12
2)
Неравенства второй степени.
.
12
2)
Неравенства второй степени.
![]() .
Случай
1.
.
Случай
1.
![]() .
.
Неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
решений нет |
решений нет |
|
Случай
2.
![]() .
.
Неравенство |
|
|
|
|
|
|
|
|
|
|
решений нет |
решений нет |
|
|
|
|
|
|
3) Рациональные уравнения и неравенства.
Многочленом
![]() -
ой степени (
-
ой степени (![]() )
от переменной
)
от переменной
![]() называется выражение
называется выражение
![]() ,
,
где
![]() – заданные действительные числа,
причем
– заданные действительные числа,
причем
![]() .
Многочленами
нулевой степени являются отличные от
нуля действительные числа. Число
.
Многочленами
нулевой степени являются отличные от
нуля действительные числа. Число
![]() единственный многочлен,
единственный многочлен,
13
степень
которого не определена.
Уравнение
![]() ,
где
,
где
![]() – многочлен
– многочлен
![]() -ой
степени,
-ой
степени,
![]() ,
называется алгебраическим уравнением
,
называется алгебраическим уравнением
![]() -ой
степени.
-ой
степени.
Если
![]() – корень многочлена
– корень многочлена
![]() ,
т.е.
,
т.е.
![]() ,
то
,
то
![]() без остатка делится на (
без остатка делится на (![]() ):
):
![]() ,
,
где
![]() –
многочлен степени
–
многочлен степени
![]() .
Многочлен
.
Многочлен
![]() можно найти либо делением «уголком»
многочлена
можно найти либо делением «уголком»
многочлена
![]() на
(
на
(![]() ),
либо группировкой слагаемых многочлена
),
либо группировкой слагаемых многочлена
![]() и выделением из них множителя
и выделением из них множителя
![]() .
Основными методами решения уравнения
.
Основными методами решения уравнения
![]() ,
где
,
где
![]() – многочлен степени
– многочлен степени
![]() (
(![]() ,
являются метод разложения левой части
уравнения на множители и метод введения
новой переменной.
Уравнение вида
,
являются метод разложения левой части
уравнения на множители и метод введения
новой переменной.
Уравнение вида
![]() ,
где
,
где
![]() и
и
![]() многочлены, называется рациональным.
Это уравнение равносильно системе
многочлены, называется рациональным.
Это уравнение равносильно системе
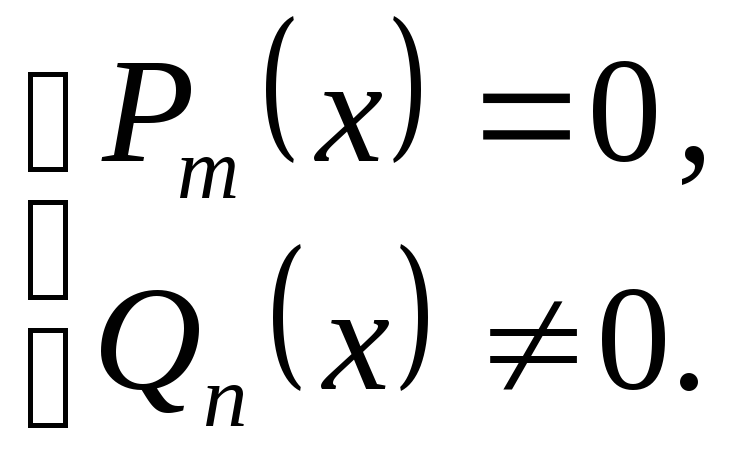 Рациональные неравенства – это
неравенства вида
Рациональные неравенства – это
неравенства вида
![]() ,
где
,
где
![]() и
и
![]() многочлены. Основной метод решения
рациональных неравенств – метод
интервалов.
Рассмотрим
сначала неравенство
многочлены. Основной метод решения
рациональных неравенств – метод
интервалов.
Рассмотрим
сначала неравенство
![]() .
Находим корни уравнения
.
Находим корни уравнения
![]() .
Пусть
.
Пусть
![]() корни этого уравнения, расположенные
в порядке возрастания.
корни этого уравнения, расположенные
в порядке возрастания.
Числовая
прямая точками
![]() разбивается на ин-
разбивается на ин-
14
т ервалы,
в каждом из которых функция
ервалы,
в каждом из которых функция
![]() сохраняет знак.
сохраняет знак.
Для определения знаков значений функции в полученных интервалах достаточно найти знак значения функции в любой точке соответствующего интервала.
Множеством
всех решений неравенства
![]() будет объединение всех промежутков, в
которых функция
будет объединение всех промежутков, в
которых функция
![]() сохраняет отрицательный знак.
сохраняет отрицательный знак.
Имеют
место следующие соотношения:
![]() ,
,
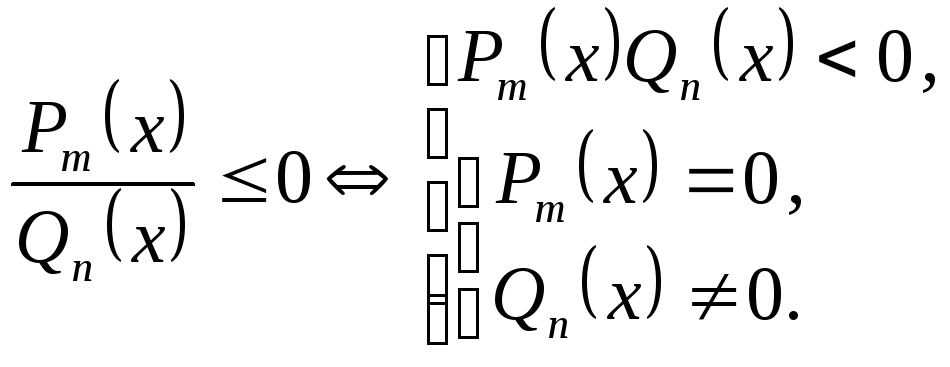 Аналогично решаются неравенства вида
Аналогично решаются неравенства вида
![]() .
Пример 1.
Решить уравнение
.
Пример 1.
Решить уравнение
![]() .
.
Решение.
Перепишем уравнение в виде
![]() .
Но
.
Но
![]() и
и
![]() .
Поэтому получаем:
.
Поэтому получаем:
![]()
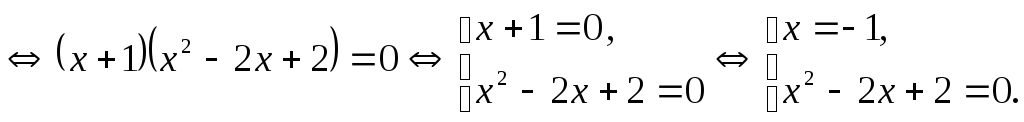 Квадратное
уравнение
Квадратное
уравнение
![]() корней не имеет
(т.к.
корней не имеет
(т.к.![]() ).
Следовательно, исходному уравнению
удовлетворяет только значение
).
Следовательно, исходному уравнению
удовлетворяет только значение
![]() .
.
Ответ: – 1.
15
Пример
2. Найти сумму
корней уравнения:
![]() .
Решение.
Так как
.
Решение.
Так как
![]()
![]() ,
то исходное уравнение принимает вид:
,
то исходное уравнение принимает вид:
![]() .
(3)
Обозначим
.
(3)
Обозначим
![]() .
Тогда уравнение (3) принимает вид:
.
Тогда уравнение (3) принимает вид:
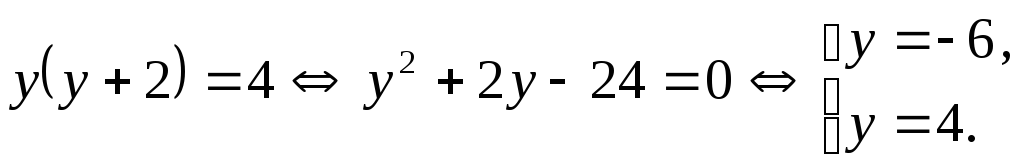
Исходное
уравнение равносильно совокупности
уравнений:
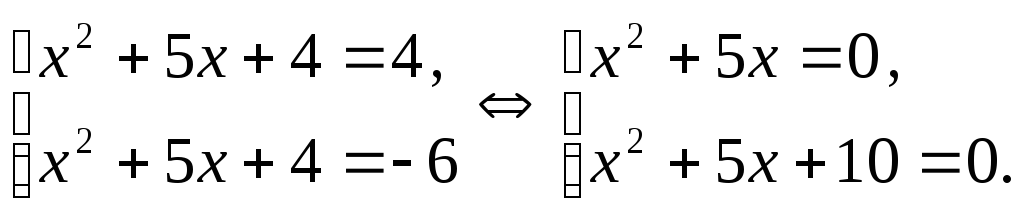
Первое
уравнение имеет корни
![]() , а второе уравнение корней не имеет (
, а второе уравнение корней не имеет (
![]() ).
).
![]() .
.
Ответ: – 5.
Пример
3. Решить
уравнение
![]() .
(4)
Решение.
Квадратный трехчлен
.
(4)
Решение.
Квадратный трехчлен
![]() обращается в нуль при
обращается в нуль при
![]() и
и
![]() ;
поэтому
;
поэтому
![]() .
(4)
.
(4)![]()
![]()
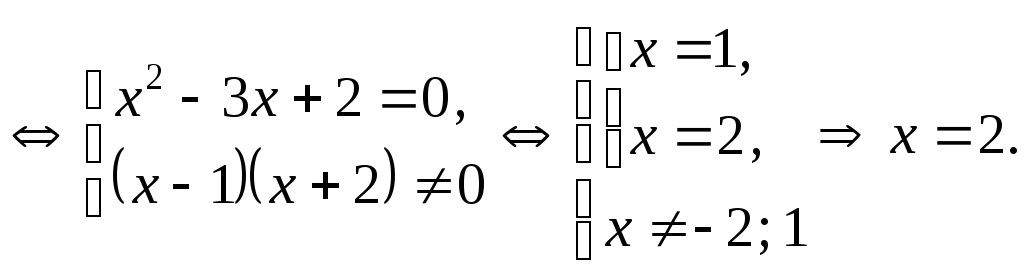
Ответ: 2.
16
Пример
4. Найти сумму
корней уравнения
![]() .
(5)
Решение.
ОДЗ уравнения (5):
.
(5)
Решение.
ОДЗ уравнения (5):
![]() .
.
При
![]() числитель дроби, стоящей в левой части
уравнения, обращается в
числитель дроби, стоящей в левой части
уравнения, обращается в
![]() :
:
![]() .
Следовательно, многочлен
.
Следовательно, многочлен
![]() без остатка делится на
без остатка делится на
![]() :
:
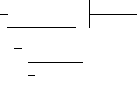

![]() .
.
Уравнение
(5) можно представить в виде:
![]() .
.
При
![]() это уравнение равносильно уравнению
это уравнение равносильно уравнению
![]() .
Корни последнего уравнения:
.
Корни последнего уравнения:
![]() .
.
![]() Ответ:
1.
Пример 5.
Найти сумму целых решений неравенства
Ответ:
1.
Пример 5.
Найти сумму целых решений неравенства
![]() .
(6)
.
(6)
17
Решение.
(6)![]()
![]() .
.
Р ешениями
последнего
ешениями
последнего
![]() неравенства являются
все числа из множества
неравенства являются
все числа из множества
![]()
Целые
решения неравенства (6):
![]() ;
;
![]() ;
;
![]()
![]() Ответ:
Ответ:
![]()
 Пример
6. Найти
наименьшее целое решение неравенства:
Пример
6. Найти
наименьшее целое решение неравенства:
![]() .
(7)
Решение.
(7)
.
(7)
Решение.
(7)
![]()
![]()
![]() .
.
Применяя
метод интервалов,
получим множество
решений
исходного неравенства:
![]() .
.
Наименьшее
целое решение:
![]() .
.
Ответ: 0.
Заметим,
что в процессе решения предыдущей задачи
может возникнуть желание упростить
неравенство
![]() ,
(8)
сократив числитель и
знаменатель дроби на
,
(8)
сократив числитель и
знаменатель дроби на
![]() .
Такое уп-
.
Такое уп-
18
рощение,
сделанное без всяких ограничений,
приведет к ошибке. Неравенство
![]() неравносильно неравенству (8), так как
число
неравносильно неравенству (8), так как
число
![]() входит в множество его решений, не
являясь в то же время решением неравенства
(8).
входит в множество его решений, не
являясь в то же время решением неравенства
(8).
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.
Найти сумму
корней уравнения:
а)
![]() .
(Ответ:
0)
.
(Ответ:
0)
б)
![]() .
(Ответ:
.
(Ответ:
![]() )
)
2.
Решить уравнение:
а)
![]() .
(Ответ:
–1)
.
(Ответ:
–1)
б)
![]() .
(Ответ:
–1)
.
(Ответ:
–1)
в)
![]() .
(Ответ:
2)
.
(Ответ:
2)
г)
![]() .
(Ответ:
–8; 4)
.
(Ответ:
–8; 4)
д)
![]() .
(Ответ:
–2)
.
(Ответ:
–2)
е)
![]() .
(Ответ:
–0,75)
.
(Ответ:
–0,75)
ж)
![]() .
(Ответ:
1)
.
(Ответ:
1)
19
3.
Найти меньший корень уравнения:
а)
![]() .
(Ответ:
– 4)
.
(Ответ:
– 4)
б)
![]() .
(Ответ:
– 5)
.
(Ответ:
– 5)
в)
![]() .
(Ответ:
0,5)
.
(Ответ:
0,5)
г)
![]() .
(Ответ:
– 10)
4.
Найти
наименьшее целое значение
.
(Ответ:
– 10)
4.
Найти
наименьшее целое значение
![]() ,
удовлетворяющее
,
удовлетворяющее
неравенству:
а)
![]() .
(Ответ:
– 3)
.
(Ответ:
– 3)
б)
![]() .
(Ответ:
2)
.
(Ответ:
2)
в)
![]() .
(Ответ:
– 10)
.
(Ответ:
– 10)
г)
![]() .
(Ответ:
2 )
.
(Ответ:
2 )
д)
![]() .
(Ответ:
3 )
.
(Ответ:
3 )
е)
![]() .
(Ответ:
– 1)
.
(Ответ:
– 1)
ж)
![]() .
(Ответ:
8 )
.
(Ответ:
8 )
5.
Найти сумму целых решений неравенства:
![]() .
(Ответ:
0 )
.
(Ответ:
0 )
20
6.
Найти сумму целых решений неравенства,
принадлежащих
отрезку
![]() :
:
а)
![]() .
(Ответ:
– 48)
.
(Ответ:
– 48)
б)
![]() .
(Ответ:
3)
.
(Ответ:
3)
в)
![]() .
(Ответ:
460)
г)
.
(Ответ:
460)
г)
![]() .
(Ответ:
– 440)
.
(Ответ:
– 440)
21