
Параметрическое программирование
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
“Кузбасский государственный технический университет”
Кафедра вычислительной техники и информационных технологий
ПАРАМЕТРИЧЕСКОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Методические указания и задания для практических занятий и самостоятельной работы студентов экономических специальностей
по дисциплинам “Исследование операций в экономике” и “Экономико-математические методы и модели”
Составители М. А. Тынкевич Г. Н. Речко
Утверждены на заседании кафедры Протокол № 5 от 03.12.2009
Рекомендованы к печати учебно-методической комиссией специальности 080801 Протокол № 5 от 03.12.2009
Электронная копия хранится в библиотеке ГУ КузГТУ
КЕМЕРОВО 2010
1
Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.
Необходимость рассмотрения подобных задач обусловлена различными причинами, основная из которых связана с тем, что исходные данные для численного решения любой реальной задачи оптимизации практически всегда определяются приближенно или могут изменяться под влиянием каких-то факторов, что может существенно сказаться на оптимальности выбираемой программы (плана) действий. В роли таких факторов могут выступать время, температура, курс доллара по отношению к рублю, цена на сырье, удаленность от поставщиков и др. Соответственно, чтобы быть готовым к изменениям ситуации (исходных данных), при решении оптимизационной задачи разумно указывать не конкретные данные, а диапазон возможного изменения данных.
С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.
Существуют различные подходы к подобному анализу. Один из них связан с т.н. постоптимальным анализом, где, отыскав оптимальный план для конкретных исходных данных, мы пытаемся выяснить диапазоны вариации этих данных, при которых найденный план остается оптимальным. Другой подход базируется на включении некоторых параметров в математическую модель и построении решения как функции от них .
Сразу оговоримся, что универсальных методов анализа устойчивости решений произвольной задачи математического программирования нет и в случае множественности параметров или нелинейных связях трудности такого анализа даже с помощью современных компьютеров исключительны.
2
Рассмотрим задачу параметрического линейного программиро-
вания, в которой только коэффициенты целевой функции линейно
зависят от некоторого единственного параметра :
отыскать максимум (или минимум) функции
n
L ( X , ) = ( C j + D j ) X j j 1
при условиях
n
A j X j |
B , |
Xj 0 , j = 1 ... n ; |
1 |
|
|
|
2 . |
j 1 |
|
|
|
|
|
|
|
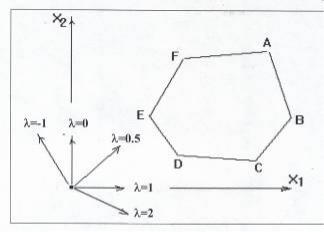
Если обратиться к геометрической интерпретации задачи, то можно заметить, что градиент линейной формы зависит от параметра. Например, для целевой функции L(X, ) = X1 + (1- )X2 при различных значениях параметра градиент определяет различные на-
правления роста функции.
Нетрудно видеть, что, если при некотором значении параметра максимум достигается в вершине A, то небольшая вариация этого значения несколько изменит направление градиента, но не изменит положение точки максимума.
Отсюда напрашивается вы-
вод, что некоторый план, оп-
тимальный при |
= 0, |
опти- |
мален и в окрестности |
0 , т. |
|
е. при , |
где 0 |
[ , |
]. |
|
|
Можно заметить, что при градиенте, ставшем перпендикулярным некоторой стороне многоугольника планов, имеем два разных оптимальных опорных плана с одним и тем же значением линейной формы, откуда можно утверждать непрерывность экстремума линейной формы по .
3
В случае неограниченности множества планов можно утверждать, что если линейная форма не ограничена при каком-то = 0 ,
то она не ограничена при всех , больших или меньших 0.
Алгоритм для решения задач параметрического линейного программирования в случае зависимости от параметра коэффициентов целевой функции незначительно отличается от обычного симплексно-
го метода (примеры решения подобных задач приведены ниже).
В случае зависимости от параметра компонент вектора пра-
вых частей ограничений, т. е. решения задачи поиска |
экстремума |
||||
функции |
|
|
|
|
|
|
|
n |
|
|
|
|
|
L ( X ) = C j |
X j |
|
|
|
|
j 1 |
|
|
|
при условиях |
|
|
|
|
|
n |
|
|
|
|
|
A j X j |
B λD , |
Xj 0 , j = 1 ... n ; |
1 |
|
2 , |
j 1 |
|
|
|
|
|
во избежание сложностей, связанных с требованием сохранения неотрицательности компонент плана при любых (сохранения неотрицательности правой части системы уравнений при всех ее тождественных преобразованиях), достаточно постановить и решить сопряженную задачу, воспользовавшись вышеупомянутым алгоритмом решения задач параметрического линейного программирования при зависимости от параметра коэффициентов целевой функции, и с помощью известных двойственных соотношений отыскать решение исходной задачи.
Пример 1. Рассмотрим задачу минимизации
L(X, ) = X1 - X2 - X3 + X4
при условиях
3X1 - 3X2 - X3 + X4 5; |
|
2X1 - 2X2 + X3 - X4 3; |
|
Xk 0 , k = 1 .. 4 ; |
- < < . |
4
Решение. Как обычно, приводим задачу к канонической форме и с использованием метода искусственного базиса отыскиваем началь-
ный опорный план X0 = (0, 0, 0, 0, 0, 3, 5) c |
L(X0, ) = 5М. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
C |
|
Базис |
План |
|
|
-1 |
1 |
0 |
0 |
M |
|
|
- |
|
|
|
|
|
|||
баз |
|
1 |
Xбаз |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
M |
|
A7 |
5 |
3 |
-3 |
-1 |
1 |
-1 |
0 |
1 |
0 |
|
A6 |
3 |
2 |
-2 |
1 |
-1 |
0 |
1 |
0 |
|
k |
5M |
3M- |
-3M+ |
-M+1 |
M-1 |
- M |
0 |
0 |
|
Так как определяющую роль на этом шаге решения играет величина M, превышающая все величины задачи, то не обращаем внимания на и, обнаружив невыполнение критерия оптимальности для
X0, вводим в базис A4 вместо A7 (переходим к следующему опорному плану):
C |
|
Базис |
План |
|
|
-1 |
1 |
0 |
0 |
баз |
|
2 |
Xбаз |
|
- |
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|||
1 |
|
A4 |
5 |
3 |
-3 |
-1 |
1 |
-1 |
0 |
0 |
|
A6 |
8 |
5 |
-5 |
0 |
0 |
-1 |
1 |
|
k |
5 |
3 - |
-3+ |
0 |
0 |
- 1 |
0 |
|
Полученный опорный план X1 = (0, 0, 0, 5, 0, 8) c L(X1, ) = 5
будет оптимальным, если все значения k неположительны, т. е.
|
1 |
3 - λ- λ 0 |
|
λ |
3 |
|
-3 + λ+ 0 |
||||
|
2 |
|
λ |
3 . |
Решаем систему двух линейных неравенств и обнаруживаем, что найденный план X1 оптимален при = 3 .
Исследуем оставшиеся из заданного диапазона значения ..
Пусть > 3 . Тогда 2 >0 и вектор A2 подлежит вводу в базис, но в силу неположительности его компонент приходим к выводу, что
при >3 линейная форма задачи не ограничена снизу.
Пусть < 3 . Тогда 1> 0 и в базис вводится вектор A1 :
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
C |
Базис |
План |
|
|
-1 |
1 |
0 |
0 |
баз |
3 |
Xбаз |
|
- |
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|||
1 |
A4 |
1/5 |
0 |
0 |
-1 |
1 |
-2/5 |
-3/5 |
|
A1 |
8/5 |
1 |
-1 |
0 |
0 |
-1/5 |
1/5 |
|
k |
(8 +1)/5 |
0 |
0 |
0 |
0 |
-( +2)/5 |
( -3)/5 |
Полученный опорный план является оптимальным, если все значения k неположительны, т. е.
|
5 = - ( + 2 )/5 0 |
|
- 2 |
. |
|
6 = ( 3 ) / 5 0 |
|
3 |
|
|
|
|
Очевидно, что найденный план X=(8/5, 0, 0, 1/5) c L(X, ) =(8 +1)/5 оптимален при -2 3.
Пусть < - 2 . Тогда 5 > 0 и вектор A5 подлежит вводу в базис; в силу неположительности его компонент приходим к выводу, что при < - 2 линейная форма задачи не ограничена снизу.
Таким образом, мы получили решение задачи:
|
- , |
|
( 8 λ+1 )/ 5, |
|
|
Lmin(X, ) = |
5, |
|
|
|
- , |
|
λ -2; |
|
|
2 λ 3; |
X opt ( 8 / 5 |
, 0 , 0 , 1/ 5 ); |
λ 3 ; |
X opt= ( 0 |
, 0 , 0, 5 ); |
λ 3 . |
|
|
|
Пример 2. Рассмотрим задачу минимизации |
|
|
||||||||||
|
|
|
|
L(X, ) = (2- ) X1 - 3 X2 +( -3)X3 |
|
||||||||
при условиях |
|
X1 + |
X2 + |
|
X3 |
5; |
|
|
|||||
|
|
|
|
|
3 X1 – X2 – 2 X3 6; |
|
|
||||||
|
|
|
|
|
X1 + 2 X2 + 2 X3 8; |
|
|
||||||
|
|
|
|
|
Xk 0 , k = 1 .. 3; |
- < < . |
|||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|||
|
C |
|
Базис |
План |
2- |
-3 |
|
|
-3 |
0 |
0 |
0 |
|
|
баз |
|
1 |
Xбаз |
|
|
|
||||||
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
||||||
|
0 |
|
A4 |
5 |
1 |
1 |
|
1 |
1 |
0 |
0 |
||
|
0 |
|
A5 |
6 |
3 |
-1 |
|
-2 |
0 |
1 |
0 |
||
|
0 |
|
A6 |
8 |
1 |
2 |
|
2 |
0 |
0 |
1 |
||
|
|
k |
0 |
-2 |
3 |
|
3- |
0 |
0 |
0 |
|||
6
Находим начальный опорный план задачи X0 = (0, 0, 0, 5, 6, 8) c
L(X0, ) =0, который был бы оптимален при выполнении условий: |
|||
1 = -2 0 , |
2 = |
3 0, |
3 = 3- 0 . |
Однако попытка решения этой системы трех линейных неравенств
обнаруживает её противоречивость ( |
2 , 0, |
3 ). |
|
|
||||||||||||||||||||
|
Пусть < 3. Тогда |
3 > 0 |
|
и вводим в базис A3: |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
C |
|
Базис |
|
План |
|
|
2- |
|
|
|
-3 |
-3 |
|
0 |
|
0 |
0 |
|
|||||
|
баз |
|
2 |
|
Xбаз |
|
|
A1 |
|
|
|
|
|
A2 |
A3 |
|
A4 |
|
A5 |
A6 |
|
|||
|
0 |
|
A4 |
|
1 |
|
|
1/2 |
|
|
|
|
|
0 |
|
0 |
|
1 |
|
0 |
-1/2 |
|
||
|
0 |
|
A5 |
|
14 |
|
|
4 |
|
|
|
|
|
1 |
|
0 |
|
0 |
|
1 |
1 |
|
||
|
-3 |
|
A3 |
|
4 |
|
|
1/2 |
|
|
|
|
|
1 |
|
1 |
|
0 |
|
0 |
1/2 |
|
||
|
|
|
k |
|
4( -3) |
|
(3 -7)/2 |
|
|
|
4 -3 |
0 |
|
0 |
|
0 |
( -3)/2 |
|
||||||
Полученный опорный план оптимален, если |
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
= (3 -7)/2 |
0 , |
2 = 4 -3 |
0, |
|
|
|
6 |
= |
( -3)/2 |
0 . |
||||||||||||
|
Решение этой системы неравенств обнаруживает, что план |
|||||||||||||||||||||||
X=(0,0,4) c L(X, ) = 4( -3) |
оптимален |
при |
3/4. |
|
|
|
||||||||||||||||||
|
Пусть > 3/4 . Тогда |
2 > 0 и вводим в базис A2: |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
Базис |
|
План |
|
|
2- |
|
|
-3 |
|
|
-3 |
|
0 |
|
0 |
0 |
|
||||
|
баз |
|
3 |
|
Xбаз |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
A1 |
|
|
|
|
|
A2 |
A3 |
|
A4 |
|
A5 |
A6 |
|
||||||
|
0 |
|
A4 |
|
1 |
|
|
1/2 |
|
|
|
|
|
0 |
|
0 |
|
1 |
|
0 |
-1/2 |
|
||
|
0 |
|
A5 |
|
10 |
|
|
7/2 |
|
|
|
|
|
0 |
|
-1 |
|
0 |
|
1 |
1/2 |
|
||
|
-3 |
|
A2 |
|
4 |
|
|
1/2 |
|
|
|
|
|
1 |
|
1 |
|
0 |
|
0 |
1/2 |
|
||
|
|
|
k |
|
-12 |
|
-( +4)/2 |
|
|
|
|
|
0 |
-4 +3 |
0 |
|
0 |
-3 /2 |
|
|||||
|
Полученный |
план оптимален, если |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 = -( +4)/2 0 , |
3 = |
|
- 4 +3 |
0 , |
6 = |
-3 /2 0 . |
||||||||||||||||
Решение системы трех неравенств обнаруживает, что план |
X = (0, 4, |
|||||||||||||||||||||||
0) c L(X, )= -12 оптимален при всех 3/4 . |
|
|
|
|
|
|||||||||||||||||||
|
Таким образом, рассмотрен весь диапазон значений . Задача |
|||||||||||||||||||||||
решена: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
X opt |
( 0 , 0 , 4 ), |
|
|
|||||||
|
|
|
|
|
4( - 3), λ |
|
4 |
; |
|
|
|
|||||||||||||
|
|
|
Lmin ( X , ) = |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
- 12 , λ |
|
х; |
X |
opt |
( 0 , 4 , 0 ). |
|
|
||||||||||||
|
|
|
|
|
4 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 3. Рассмотрим задачу максимизации
L(X, ) = X1 - X2 - 2 X3
|
7 |
|
|
|
|
при условиях |
X1+ X2 + X3 |
3 + ; |
|
||
|
2 X1 - X2 + X3 5 - ; |
|
|||
|
Xk 0 , k = 1 .. 3; |
- < < . |
|||
Решение. Чтобы решить эту задачу, достаточно решить двойст- |
|||||
венную к ней задачу, имеющую вид: |
|
|
|
||
минимизировать |
L(Y, ) = (3+ ) Y1 + (5- ) Y2 |
||||
при условиях |
Y1 |
+ 2 Y2 |
1; |
|
|
|
Y1 |
- |
Y2 |
-1; |
|
|
Y1 |
+ |
Y2 |
-2; |
|
|
|
Y1 , Y2 |
0 ; |
|
|
|
- < < . |
|
|||
Приводим двойственную задачу к канонической форме (умно- |
|||||
жив предварительно второе и третье неравенства на |
-1) и начинаем |
||||
обычное решение обычным симплексным методом. Заметьте, что ука-
занное умножение тождественно смене знака у переменных |
x2 и x3 |
|||||||||||||||
исходной задачи. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
Базис |
|
План |
3+ |
|
5- |
0 |
0 |
0 |
|
M |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
баз |
|
1 |
|
Yбаз |
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
|
A5 |
|
A6 |
||||||||
|
M |
|
A6 |
|
1 |
1 |
|
2 |
-1 |
0 |
0 |
|
1 |
|
||
|
0 |
|
A4 |
|
1 |
-1 |
1 |
0 |
1 |
0 |
|
0 |
|
|||
|
0 |
|
A5 |
|
2 |
-1 |
-1 |
0 |
0 |
1 |
|
0 |
|
|||
|
|
k |
|
M |
M -3- |
2M-5+ -M |
0 |
0 |
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
Базис |
|
План |
3+ |
|
5- |
0 |
0 |
0 |
|
M |
|
||
|
баз |
|
2 |
|
Yбаз |
|
|
|
|
|||||||
|
|
|
A1 |
A2 |
A3 |
|
A4 |
|
A5 |
|
A6 |
|
||||
|
3+ |
|
A1 |
|
1 |
1 |
|
2 |
-1 |
0 |
0 |
|
1 |
|
||
|
0 |
|
A4 |
|
2 |
0 |
|
3 |
-1 |
1 |
0 |
|
1 |
|
||
|
0 |
|
A5 |
|
3 |
0 |
|
1 |
-1 |
0 |
1 |
|
1 |
|
||
|
|
Zk |
|
3+ |
3+ |
6+2 |
-(3+ ) |
|
0 |
0 |
|
3+ |
|
|||
|
|
k |
|
0 |
|
1+3 |
-(3+ ) |
0 |
0 |
|
-M+.. |
|
||||
|
|
|
|
|
|
|
||||||||||
|
Найденный |
план Y=(1, 0) |
оптимален, |
если |
|
2 |
= |
(1+3 ) 0 |
||||||||
и 3 = -(3+ ) 0 , |
т. е. при -3 -1/3 |
Yopt =(1, 0). |
|
|
|
|
|
|||||||||
8
В строке Zk (в позициях 6, 4 и 5 в соответствии с начальным ба-
зисом) находим решение прямой задачи: Xopt =( 3+ , -0 , -0 ) , L(Xopt) = 3+ .
Пусть <-3 . Попытка ввода в базис вектора A3 обнаруживает, что в этом случае линейная форма решаемой (двойственной) задачи не ограничена снизу и, следовательно, ограничения исходной задачи
противоречивы.
В случае > -1/3 имеем:
C |
Базис |
План |
|
|
0 |
0 |
0 |
M |
баз |
3 |
Yбаз |
3+ |
5- |
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|||
5 - |
A2 |
1/2 |
1/2 |
1 |
-1/2 |
0 |
0 |
1/2 |
0 |
A4 |
1/2 |
-3/2 |
0 |
1/2 |
1 |
0 |
-1/2 |
0 |
A5 |
5/2 |
-1/2 |
0 |
-1/2 |
0 |
1 |
1/2 |
|
Zk |
( 5- )/2 |
(5- )/2 |
5 - |
-(5- )/2 |
0 |
0 |
(5- )/2 |
|
k |
-(3 +1)/2 |
0 |
-(5- )/2 |
0 |
0 |
-M+... |
|
|
|
|
Решив систему неравенств |
|
|
|
|
|
|
|||
|
|
|
|
1 = -(3 +1)/2 0 , |
|
|
|
|||
|
|
|
|
3 = -(5- )/2 0., |
|
|
|
|
|
|
обнаруживаем, что при -1/3 5 |
Yopt = (0, 1/2), |
Xopt |
= ( (5- )/2, |
|||||||
-0, -0) , L(Xopt) = (5- )/2 . |
|
|
|
|
|
|
|
|||
|
Продолжаем решение задачи при > 5 . Получаем: |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
C |
Базис |
План |
|
|
0 |
|
0 |
0 |
M |
|
|
|
|
3+ |
5- |
|
|
|
|
|
|
баз |
4 |
Yбаз |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|
|
5 - |
A2 |
1 |
-1 |
1 |
0 |
|
1 |
0 |
0 |
|
0 |
A3 |
1 |
-3 |
0 |
1 |
|
2 |
0 |
-1 |
|
0 |
A5 |
3 |
-2 |
0 |
0 |
|
1 |
1 |
0 |
|
Zk |
|
5- |
-(5- ) |
5 - |
0 |
|
5 - 0 |
0 |
|
|
k |
|
|
-8 |
0 |
0 |
|
5 - |
0 |
-M |
Видим, что
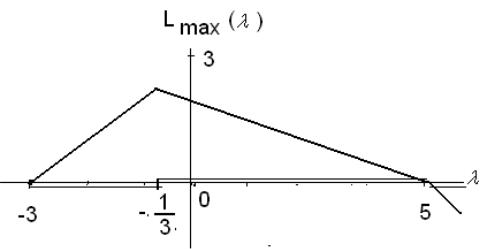
при 5 Yopt = (0, 1), Xopt=(0, -5+ , -0), L(Xopt) = 5- .
Интервал значений параметра исчерпан, выявлены четыре интервала устойчивости оптимальных решений задачи.
9
Диапазон |
Сопряженная |
Исходная задача |
||
|
|
задача |
|
|
< -3 |
L(Y, ) → - ∞ |
ограничения противоречивы |
||
|
|
|
|
|
-3 -1/3 |
Yopt = (1, 0) |
Xopt = (3+ , 0 , 0), |
L(Xopt) = 3+ |
|
|
|
|
||
-1/3 5 |
Yopt =(0, 1/2) |
Xopt = ( (5- )/2, 0, 0), L(Xopt) = (5- )/2 |
||
|
|
|
|
|
|
5 |
Yopt = (0, 1) |
|
|
|
|
Xopt = (0, -5+ , 0), |
L(Xopt) = 5- |
|
Увы, в случае зависимости от параметра компонент матрицы ограничений столь простого универсального подхода к решению не существует.
Из рассмотренных примеров видно, что иногда на начальных этапах возникают противоречивые системы неравенств. Во избежание этого можно начинать процесс с поиска оптимального плана для min
(или max). Отыскав таковой, можно приступать к последующему анализу подинтервалов оптимальности. Такой подход является естественным и при программной реализации задачи.
