1. Понятие множества

Множество – определенная совокупность объектов.

Объекты, из которых состоит множество, называются элементами

множества.

Множество не содержащее ни одного элемента называется пустым (обозначается: Ø).

Множества из элементов которого составляем конкретное множество называется универсальным(обозначается: U).

Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:

1)Перечислением всех элементов множества в фигурных скобках.

2)Характеристическим предикатом, который описывает свойство всех элементов, входящих в множество. Характеристический предикат записывается после двоеточия или символа « | ».

Операции над множествами

1)Сравнение множеств

Множество А называется подмножеством множества В, если все элементы множества А содержатся во множестве В.

Два множества называются равными, если они содержат одинаковые наборы элементов.

2) Объединением двух множеств называется множество, содержащее все элементы обоих множеств.

состоящее из общих элементов обоих множеств.

4)Разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В.

5)Симметрической разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В и всех элементов множества В не содержащихся в А.

7) Прямым или декартовым произведением множеств A и B, называется множество всех упорядоченных пар (a, b), где первый элемент a из множества A, а второй элемент b из множества B.

Степенью множества называется декартовое произведение множества A само на себя n раз.

ПРИМЕР

, .

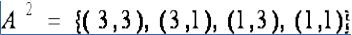
Свойства операций над множествами

1)Коммутативность.

2)Ассоциативность.

3)Дистрибутивность.

4)Закон поглощения.

5)Идемпотентность.

6)Инволютивность.

7)Свойство нуля.

АØ=А

АØ= Ø

8)Свойство единицы.

9)Закон де Моргана

2. Два множества называются равными тогда и только тогда, когда каждое из них является подмножеством другого.

Если между элементами двух множеств можно установить взаимно однозначное соответствие, то говорят, что эти множества равномощные (или эквивалентны). Два конечных множество равномощные тогда и только тогда, когда они имеют оно и тоже число элементов. Понятие равномощности применимо и к множествам, не являющимся конечными.

Законы алгебры множеств

Для операций объединения, пересечения и дополнения выполняются следующие законы:

1.коммутативности:

2.ассоциативности:

3.дистрибутивности:

oпересечения относительно объединения:

oобъединение относительно пересечения:

4.идемпотентности:

5.действия с универсальным и пустым множествами:

При положительных n Декартова степень Xn состоит из всех упорядоченных н аборов (кортежей) элементовиз X длины n.

При n = 0, Декартова степень X0 по определению содержит единственный эле мент — пустой кортеж.

5. Конечное множество состоит из конечного числа эпементов, пусть их М штук.

Подмножеств, состоящих из 1 эл-та, будет М штук, из 2 эл-тов - число сочетаний из М по 2, по 3 эл-та - будет число сочетаний из М по 3, и т. д. Сюда еще включают "несобственные подмножества", а именно, пустое, и всё множество А.

Всего получится сумма С (М, 0)+С (М, 1)+С (М, 2)+...+С (М, М) . Известно, что такая сумма равна 2M.

Примечание: Этот факт следует из формулы бинома Ньютона, так как (1+1)^M=2M.

6. Принципом включения и исключения называется формула, позволяющая вычислить мощность объединения множеств, если известны их мощности и мощности всех пересечений.

Рассмотрим частные случаи этой формулы для двух и трех множеств:

Справедливы аналогичные формулы и для пересечения множеств:

7. Бинарным отношением между множествами А и В называется подмножество R прямого произведения А х В. В том случае, когда

А = В, мы говорим просто об отношении R на А.

Способы задания:

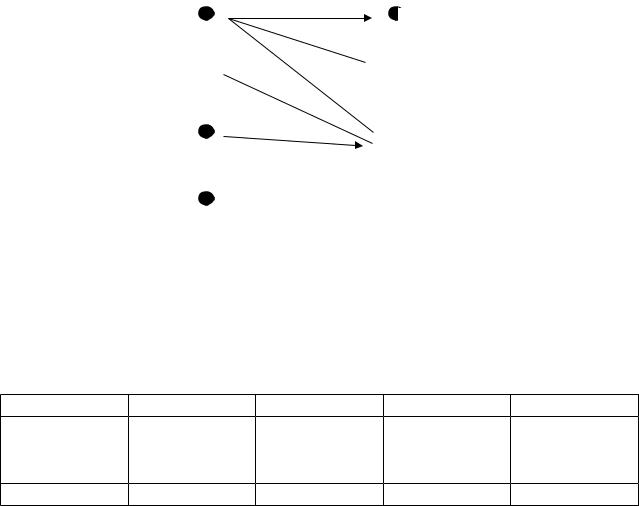
1. С помощью упорядоченных пар.

Выпишите упорядоченные пары, принадлежащие следующим бинарным отношениям на множествах А = {1,3,5, 7} и В = {2, 4, 6}:

(а)U = {{х, у): х + у = 9};

(б) V = {(x, у): х< у). Решение.

(а)U состоит из пар: (3, 6), (5, 4) и (7, 2);

(б) V = {(1, 2), (1,4), (1,6), (3,4), (3,6), (5,6)}.

2. С помощью ориентированного графа.

V = {(1, 2), (1,4), (1,6), (3,4), (3,6), (5,6)}.

1

2

34

5

6

7

3. С помощью матрицы.

А = {a, b, c ,d}

Упорядоченные пары (a, b), (a, c), (b, c), (b, d), (c, b), (d, a), (d, b), (d, d).

В паре первая буква это срока, вторая это столбец: (b, d) строка 2, 4 сотлбец.

Свойства отношений.

Рефлексивность - это одно из свойст некоторых отношений, когда каждый элемент множества находится в данном отношении к самому себе: Для всех x ϵ A xRx.

Симметричное отношение - это такое отношение между объектами, когда наличие этого отношения влечет за собой наличие этого отношения в том случае, если объекты поменять местами; иначе говоря при симметричности отношении перестановка объектов не ведет к изменению вида отношения: если xRy → yRx для каждой пары x и y из А.

Транзитивное отношение - это такое множество, например множество А, если выполняется следующие условие: если (xRy и yRz то xRz) для любой тройки элементов x,y,z ϵ A.

Кососимметричность: если (xRy и yRx → x = y) для всех x и y из А.(дальше пригодится)

8. Рефлексивное, симметричное и транзитивное бинарное отношение на множестве А называется отношением эквивалентности. Отношение эквивалентности в некотором смысле обобщает понятие равенства.

Эквивалентные элементы (т. е. находящиеся в отношении эквивалентности), как правило, обладают какими-то общими признаками.

Приведем примеры отношения эквивалентности.

•Отношение «... имеет те же углы, что и ...» на множестве всех треугольников. Очевидно, треугольники эквивалентны относительно этого отношения тогда и только тогда, когда они подобны.

•Отношение R, заданное условием: xRy, если и только если

ху > 0 на множестве ненулевых целых чисел является отношением эквивалентности. При этом эквивалентные числа имеют одинаковый знак.

• Отношение «... имеет тот же возраст, что и ...» на множестве всех людей. «Эквивалентные» люди принадлежат к одной и той же возрастной группе.

Примеры наводят на мысль, что если на множестве задано отношение эквивалентности, то все его элементы можно естественным

способом разбить на непересекающиеся подмножества. Все элементы в любом из таких подмножеств эквивалентны друг другу в самом прямом смысле. Наличие такого разбиения — движущая сила любой классификационной системы.

Разбиением множества А называется совокупность непустых подмножеств A1, A2, ... , An множества A, удовлетворяющих следующим

требованиям:

1)A = A1U A2U ... U An;

2)Ai пересекает Aj = 0 при i не равно j .

Подмножества Ai называются блоками разбиения.

Диаграмма Венна разбиение множества А на пять блоков на рисунке. Блоки на картинке как лоскуты, не заходят один на другой. Это связано с тем, что блоки разбиения не могут иметь общих элементов.

А

А1

А2

А3

А4

А5

Как мы уже говорили, отношение эквивалентности R на множестве А задает на нем разбиение. Блоки разбиения при этом состоят из эквивалентных друг другу элементов. Мы сейчас докажем это

утверждение. Но прежде определим класс эквивалентности Еx произвольного элемента х ϵ А как подмножество Еx = {z ϵ А : zRx}.

Докажем теорему.

Теорема. Пусть R — отношение эквивалентности на непустом множестве А. Тогда различные классы эквивалентности определяют разбиение А.

Доказательство. Доказательство состоит из четырех частей.

Сначала покажем, что классы эквивалентности являются непустыми подмножествами в А. По определению, Ех — подмножество

в А, Кроме того, R — рефлексивное отношение, т.е. xRx. Следовательно, x ϵ Ех и Ех не пусто.

Далее проверим, что из xRy вытекает равенство Ех = Еу. Предположим, что xRy и возьмем произвольный z ϵ Ех. Тогда zRx и

xRy. Поскольку R — транзитивное отношение, мы получаем, что zRy. Иными словами, z ϵ Еу. Следовательно, Ех подмножество Еу.

Аналогично можно показать, что Еу подмножество Ех, откуда Ех = Еу, что и требовалось.

Теперь мы покажем, что классы эквивалентности удовлетворяют первому свойству разбиения, а именно, что А является объединением всех классов эквивалентности. Как уже отмечалось в первой части нашего доказательства, Ех — подмножество в А и поэтому объединение всех классов эквивалентности тоже будет подмножеством в А. В обратную сторону, если х ϵ А, то х ϵ Ех. В частности,

X принадлежит объединению классов эквивалентности. Значит,

иА является подмножеством нашего объединения. Следовательно, А совпадает с объединением классов эквивалентности.

И, наконец, в последней части мы покажем, что два разных класса эквивалентности не пересекаются. Этим мы проверим, что классы удовлетворяют второму свойству разбиения. Воспользуемся методом «от противного». Допустим, что Ех пересекает Еу = Ø. Тогда найдется элемент z в A, принадлежащий пересечению Ех и Еу, Следовательно, zRx и zRy. Так как R — симметричное отношение, можно утверждать, что xRz и ZRy, Ввиду транзитивности R, это влечет xRy.

Значит, по второй части доказательства, Ех = Еу. Итак, мы предположили, что разные классы эквивалентности Ех и Еу пересекаются

идоказали, что они на самом деле совпадают. Полученное противоречие доказывает последнюю часть наших рассуждений. Теорема доказана.

9. Как на словах это рассказать не знаю, но то что мы писали в лекции, то и напишу сюда.

A = Z , xRy если x2 - y2 = 3k

Докажем что:

1.Рефлексивно: x2 - x2 = 0 = 3k (как я понял что 0 делится на 3 без остатка; как Артем сказал что 0 можно представить как 3*k (как 3*0) ).

2.Симметричность: y2 - x2 = 3(-k)

3.Транзитивно: x2 - z2 = 3k; z2 - y2 = 3h; x2 - y2 = 3(k+h); {x~y| x2 - y2 = 3k} Дальше пойдет вроде как классы эквивалентности.

Z = E1 + E2 + ... + En

1) E1 = Ex = E0 = {y ϵ Z| 0~y} = {0, ±3, ±6 ... } y=3k