
- •Введение
- •1. Общая часть
- •1.3. Функциональная схема регулятора
- •1.4. Устойчивость
- •1.5. Критерий устойчивости Гурвица
- •1.6. Критерий устойчивости Михайлова
- •1.7. Построение областей устойчивости методом d-разбиения
- •1.8 Качество автоматических систем регулирования
- •Охрана труда и правила безопасности.
- •Техника безопасности при эксплуатации средств автоматизации.
- •Охрана окружающей среды.
- •Литература
1.5. Критерий устойчивости Гурвица
Наиболее распространенная в технической практике форма алгебраического критерия устойчивости известна под названием критерия Гурвица. Этот критерий формирует условия устойчивости в форме определителей.
Таблица составляется по
следующему правилу: по главной диагонали
выписываются последовательно коэффициенты
характеристического уравнения, начиная
с
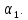 Столбцы таблицы, начиная с главной
диагонали, заполняются вверх по
возрастающим индексам, вниз по убывающим:
все коэффициенты с индексами ниже нуля
и выше степени уравнения
Столбцы таблицы, начиная с главной
диагонали, заполняются вверх по
возрастающим индексам, вниз по убывающим:
все коэффициенты с индексами ниже нуля
и выше степени уравнения заменяются нулями.
заменяются нулями.
 (1)
(1)
Его характеристическое уравнение третьей степени системы регулирования имеет вид:
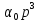 +
+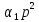 +
+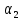 р
+
р
+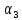 =0
(2)
=0
(2)
Условия устойчивости будут:
 ;
;
 ;
;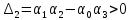 (3)
(3)
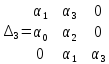 =
=
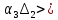 0,
0,
откуда
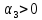
Окончательно получаем условия:
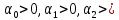 0,
0,
 0;
0;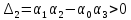 (4)
(4)
Следовательно, для устойчивости системы третьего порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительны, и чтобы определитель второго порядка был положителен.
1.6. Критерий устойчивости Михайлова
Основное преимущество частотных методов заключается в их большой наглядности.
Частотные критерии устойчивости можно разделить на 2 группы:
Характеризует устойчивость замкнутой системы;
Характеризует устойчивость разомкнутой системы.
Частотные критерии являются графико-аналитическими, они позволяют определить устойчивость замкнутой системы при отсутствии характеристического уравнения и передаточных функций системы, используя экспериментально полученные характеристики.
Для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения лежали в левой полуплоскости.
Дано характеристическое уравнение:
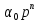 +
+
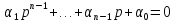 (5)
(5)
Заменяем в характеристическом уравнении комплексную переменную Р мнимой переменной jw. Получим функцию мнимого переменного jw, в которой w может принимать любое значение от +∞ до -∞.
A(j )
=
)
=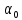 (j
(j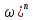 +
+ (j
(j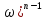 +
+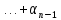 (j
(j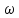 )
+
)
+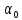 = 0 (6)
= 0 (6)
Выделяем мнимую и действительную части системы:
Re(j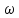 )
=
)
=
 …
- вещественная часть функцииA(j
…
- вещественная часть функцииA(j );
(7)
);
(7)
Jm(j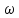 )
=
)
=
 (
(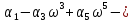 …)
- мнимая часть функцииA(j
…)
- мнимая часть функцииA(j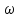 );
(8)
);
(8)
A(j )
=
)
=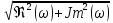 -
модуль функцииA(j
-
модуль функцииA(j );
); (9)
(9)
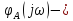 arctg
arctg
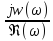 – фаза или аргумент функцииA(j
– фаза или аргумент функцииA(j ).
(10)
).
(10)
Годограф Михайлова для устойчивых систем называется правильным и имеет следующие особенности:
1.Он состоит из двух ветвей,
соответствующих изменениям от 0 до +∞
и от 0 до -∞. Ветви симметричны, так как
вещественная часть функции A(j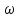 )
представляет собой четкую функцию
)
представляет собой четкую функцию
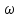 ,
а мнимая ее часть является нечетной
функцией
,
а мнимая ее часть является нечетной
функцией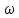 .
Поэтому достаточно исследовать только
одну ветвь годографа (измерение от 0 до
+∞).
.
Поэтому достаточно исследовать только
одну ветвь годографа (измерение от 0 до
+∞).
2.При
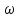 =0 получаем:
=0 получаем:
Re(j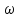 )
=
)
=
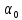 иjm(
иjm(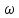 )
= 0,
)
= 0,
т. е. обе ветви годографа начинаются в точке, расположенной на положительной вещественной полуоси.
3.При изменении w
от 0 до +∞ кривая годографа поворачивается
против часовой стрелки на угол
 поочередно обходя «
поочередно обходя « »
квадрантов комплексной плоскости, где𝚗
– степень характеристического уравнения
системы.
»
квадрантов комплексной плоскости, где𝚗
– степень характеристического уравнения
системы.
Линейная система 𝚗 – го порядка устойчива, если при изменении w от 0 до ∞ годограф Михайлова последовательно обходит 𝚗 квандрантов комплексной плоскости против часовой стрелки, начинаясь в точке на положительной вещественной полуоси и нигде не проходят через начало координат.
Если годограф обходит меньше чем 𝚗 квадрантов или при обходе нарушается последовательность перехода его из квадранта в квадрант, то система будет неустойчивой.
Если годограф проходит через начало координат, система будет на границе устойчивости.
