Решение ЗЛП

4. Оптимизационные экономико-математические модели

4.1. Общая задача оптимизации

В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования предприятия, когда возникают ситуации выбора варианта, наилучшего по некоторому правилу или критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).

Отличительной особенностью оптимизационных моделей является наличие условия нахождения оптимального решения (критерия оптимальности), которое записывается в виде функционала. Эти модели при определенных исходных данных задачи позволяют получить множество решений, удовлетворяющих условиям задачи, и обеспечивают выбор оптимального решения, отвечающего критерию оптимальности.

В общем виде математическая постановка задачи математического программирования состоит в определении наибольшего или наименьшего значения целевой функции 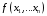при ограничениях

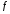, где и 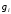- заданные функции, 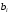- некоторые заданные числа, а - переменные, определяемые экономическое содержание задачи.

Задачи математического программирования делятся на задачи линейного и нелинейного программирования.

Если все функци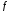и и 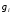линейные, то соответствующая задача является задачей линейного программирования (ЗЛП), в противном случае перед нами задача нелинейного программирования (ЗНП).

В общем виде задача линейного программирования ставится следующим образом: найти вектор максимизирующий линейную форму

141Equation Chapter 1 Section 4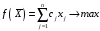 242\* MERGEFORMAT (.)

и удовлетворяющий условиям

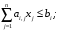343\* MERGEFORMAT (.)

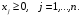444\* MERGEFORMAT (.)

Линейная функция (4.1) называется целевой функцией задачи.

Условия (4.2) называют функциональными, а (4.3) – прямыми ограничениями задачи.

Вектор 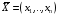, компоненты которого удовлетворяют условиям (4.2 - 4.3), будем называть планом или допустимым решением ЗЛП.

Все допустимые решения образуют область определения ЗЛП, или область допустимых решений Допустимое решение, максимизирующие целевую функцию (1), называют оптимальным планом задачи

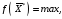545\* MERGEFORMAT (.)

где 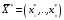- оптимальное решение ЗЛП.

На практике хорошо себя зарекомендовали оптимизационные модели определение:

• оптимальной производственной программы;

• оптимального смешения компонентов;

• оптимального раскроя;

• оптимального размещения предприятия некоторой отрасли на определенной территории;

• формирования оптимального портфеля ценных бумаг;

• транспортной задачи.

Для решения ЗЛП применяется метод последовательно улучшения плана, или симплекс-метод, который состоит из двух вычислительных процедур: симплекс-метода с естественным планом и симплекс-метода с искусственным планом (М-метод).

Выбор конкретной вычислительной процедуры осуществляется после приведения исходной задачи к каноническому виду (КЗЛП) [13]:

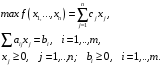646\* MERGEFORMAT (.)

Будем считать, что ЗПЛ записана в канонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные не отрицательные.

4.2. Графический метод решения Задач линейного программирования (ЗЛП)

Графический метод решения ЗЛП является наиболее простым и применяется для решения задач ЛП с двумя переменными. Рассмотрим ЗЛП в стандартной форме (4.1)-(4.3). Положим , получим

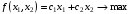(4.6)

при условиях

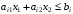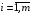, (4.7)

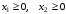
Система неравенств (4.6) совместна (имеет хотя бы одно решение). Каждое неравенство этой системы графически определяет полуплоскость, ограниченную прямой

,

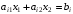условия не отрицательности определяют полуплоскости с граничными прямыми 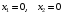(рис. 4.1).

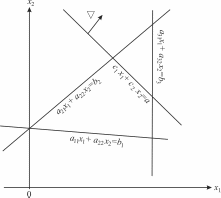
Рис. 4.1. Схема построения ОДР и вектора-градиента

Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством, координаты каждой точки которого удовлетворяют системе неравенств (4.7). Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, ограниченным и неограниченным многоугольником.

Таким образом, геометрически решение ЗЛП представляет собой отыскание такой точки многоугольника решений, координаты которой доставляют линейной функции цели.

Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор-градиент, координаты которого, являются частными производными целевой функции:

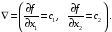747\* MERGEFORMAT (.)

Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая , перпендикулярная вектору-градиенту, является линией уровня целевой функции.

В любой точке линии уровня целевая функция принимает одно и тоже значение. Приравниваем целевую функцию постоянной величине «a». Меняя значение «a» получим семейство параллельных прямых, каждая из которых является линией уровня целевой функции (ЦФ).

Важное свойство линии уровня ЦФ состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону уровень только убывает.

С геометрической точки зрения в ЗЛП ищется такая угловая точка или набор точек допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Графический метод решения ЗЛП состоит из следующих этапов:

• строится многоугольная ОДР ЗЛП;

• строится вектор-градиент ЦФ в какой-нибудь точке 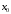, принадлежащей ОДР: ;

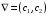• линии уровня 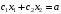(а – постоянная величина) – прямая, перпендикулярная вектору-градиенту 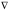, – передвигается в направлении этого вектора в случае максимизации 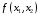до тех пор, по не покинет ОДР. Предельная точка (или точки) области при этом движении является точкой максимума ;

• для нахождения координат точки максимума достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение 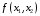, найденное в получаемой точке, является максимальным.

При минимизации (максимизации) функци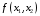и линия уровня перемещается в направлении, противоположному вектору-градиенту. Если прямая, соответствующая линии уровня, при своем движении не покидает ОДР, то минимум (максимум) функции 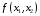не существует.

Если линия уровня параллельна какому-либо ограничению задачи, то оптимальное значение ЦФ будет двигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и соответственно, любая из этих точек является оптимальным решением задачи.

Возможные ситуации графического решения ЗЛП представлены в табл. 4.1.

Таблица 4.1

Возможные ситуации графического решения ЗЛП

№	Вид ОДР	Вид оптимального решения
1	Ограниченная	Единственное решение
		Бесконечное множество решений
2	Неограниченная	ЦФ не ограничена снизу
		ЦФ не ограничена сверху
		Единственное решение
		Бесконечное множество решений
3	Отрезок	Единственное решение
		Бесконечное множество решений

Рассмотрим графическое решение задач линейного программирования на следующем примере.

Пример 4.1. Планирование выпуска продукции пошивочного предприятия.

Намечается выпуск костюмов двух видов – женских и мужских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 чел./день трудозатрат. На мужской костюм – 3,5 м шерсти, 0,5 м лавсана и 1 чел./день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 чел./дней трудозатрат. Требуется определить, сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского – 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.

Экономико-математическая модель задачи

Введем обозначения: 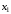– число женских костюмов; 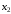– число мужских костюмов. Прибыль от реализации женских костюмов составляет , а от реализации мужских – 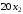, т.е. необходимо максимизировать целевую функцию:

.

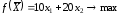Ограничения задачи имеют вид:

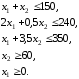
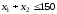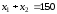Первое ограничение по труду . Прямая проходит через точк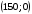и и 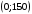(рис. 4.2).

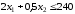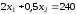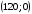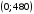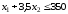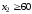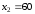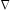Второе ограничение по лавсану . Прямая проходит через точки и . Третье ограничение по шерсти , стоится аналогично. Добавим четвертое ограничение по количеству мужских костюмов . Решением этого неравенства является полуплоскость, лежащая выше прямой . На рис. 4.3 заштрихована область допустимых решений. Для определения направления движения к оптимуму построим вектор градиент , координаты которого являются частными производными целевой функции, т.е.

.

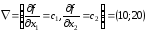Чтобы построить такой вектор, нужно соединить точку 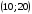с началом координат. При максимизации целевой функции необходимо двигаться в направлении вектора-градиента, а при минимизации – в противоположном направлении. Для удобства можно построить вектор, пропорциональный вектору-градиенту. Так, на рис. 4.4 изображен вектор-градиент .

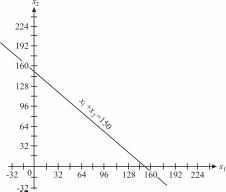
Рис. 4.2. Решением первого неравенства является нижняя полуплоскость

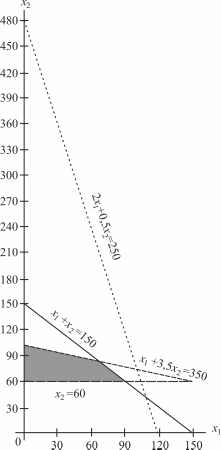
Рис. 4.3. Заштрихована область допустимых решений

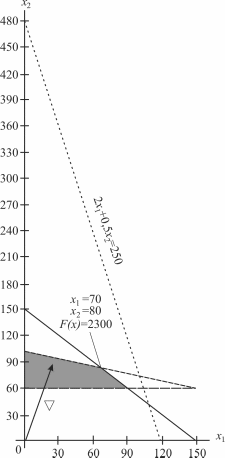
Рис. 4.4. Максимум целевой функции достигается в точке (70; 80)

В нашем случае движение линии уровня будем осуществлять до ее выхода из области допустимых решений. В крайней, угловой, точке достигается максимум целевой функции. Для нахождения координат этой точки достаточно решить систему из двух уравнений прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума:

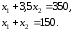
Отсюда легко записать решение исходной ЗЛП: 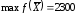и достигается пр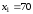и и 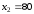(рис. 4.4).