
КИНЕМАТИКА
.pdf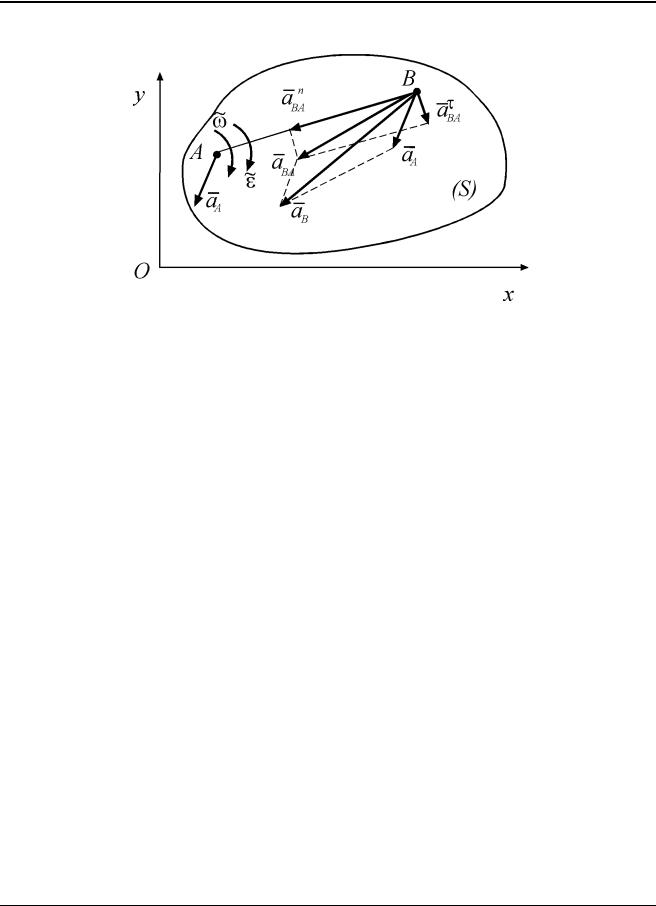
4. Сложное движение точки
Рис. 3.8
4. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
АБСОЛЮТНОЕ, ОТНОСИТЕЛЬНОЕ И ПЕРЕНОСНОЕ ДВИЖЕНИЯ ТОЧКИ
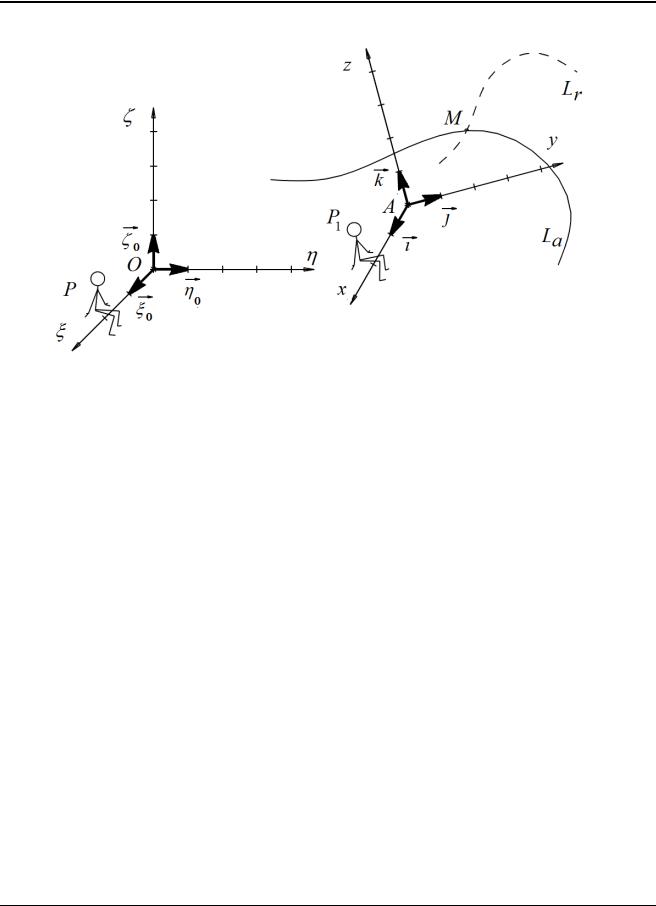
Пусть движение точки М одновременно исследуется в двух пространствах, движущихся известным образом одно в другом. Одно из этих пространств, например O , назовем неподвижным или абсолютным, а другое – Axyz – подвижным или относительным.
Движение точки М в неподвижном пространстве называют ее абсолютным движением, а в подвижном – относительным. Траектории La и Lr , скорости va
и vr ускорения aa и ar точки в этих двух ее движениях называются соответственно абсолютными и относительными.
Точку M1 подвижного пространства, которая в данный момент времени совпадает с рассматриваемой точкой М назовем совпадающей точкой.
Движение этой совпадающей точки подвижного пространства в неподвижном пространстве назовем переносным движением точки.
30
4. Сложное движение точки
Рис. 4.1
Кривая Le , которую точка М1 очертит в неподвижном пространстве, назы-
вается траекторией переносного движения точки. Скорость ve и ускорение ae точки М в переносном движении называются переносными.
Постановка задачи о сложном движении точки
Пусть известно движение точки в подвижном пространстве и его движение в неподвижном пространстве требуется найти движение точки в неподвижном пространстве.
Эта задача называется задачей о сложении движений точки.
Иначе: по известным относительному и переносному движениям точки надо найти ее абсолютное движение.
Если же известно абсолютное движение точки и требуется при известном её переносном движении найти относительное или при известном её относительном движении найти переносное, то это будет задача разложения движений.
Задача об установления связей между кинематическими характеристиками точки в двух пространствах, а значит задача о сложении движений точки, решается с помощью теорем сложения скоростей и ускорений.
31

4. Сложное движение точки
СВЯЗЬ МЕЖДУ ПРОИЗВОДНЫМИ ВЕКТОРА В ДВУХ ПРОСТРАНСТВАХ
Пусть мерой физического процесса, изучаемого наблюдателями из неподвижного и подвижного пространств, служит вектор u u t .
|
d |
|
|
|
du |
|
Обозначим через |
u |
|
и |
про- |
||
dt |
|
dt |
||||
|
|
|
|
|||
изводные по времени вектора U в неподвижном O и подвижном Axyz пространствах. Первую из них назовем абсолютной, вторую – относительной.
Чтобы установить связь между этими двумя производными, предложим каждому из наблюдателей продифференцировать формулу разложения
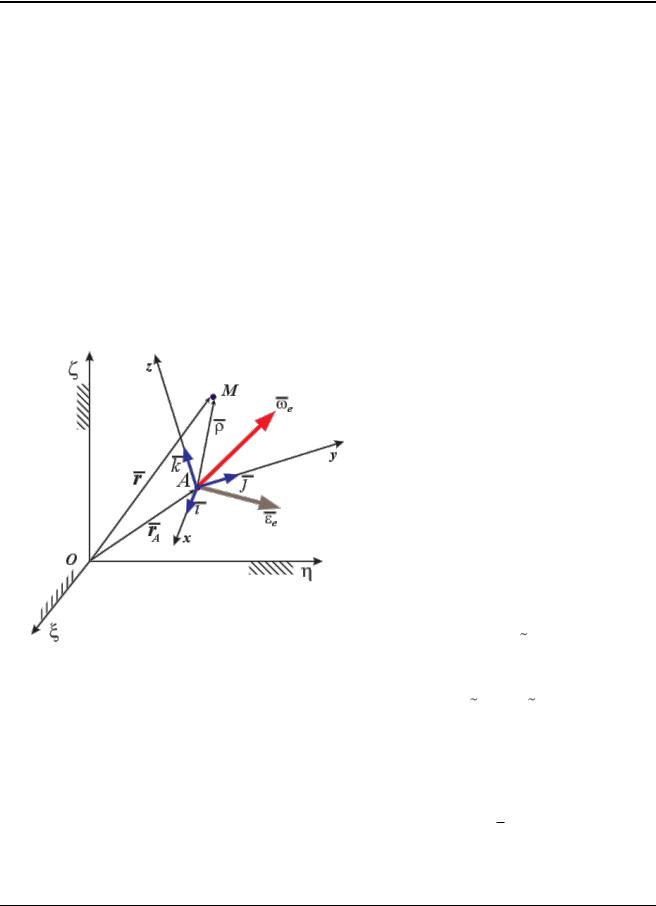
Рис. 4.2 |
u iux juy kuz |
|
вектора U по осям координат подвижного пространства Axyz .
В результате получаются следующие выражения для относительной и абсолютной производных вектора:
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iu |
x |
|
ju |
y |
|
ku |
z |
(4.1) |
|||||
|
||||||||||||||
dt |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
iu |
|
|
|
|
|
|
|
d i |
|
|
|
d j |
u |
|
dk |
. |
|
|||||
u |
|
ju |
|
ku |
|
u |
|
|
u |
|
|
(4.2) |
|||||||||||||
|
|
|
x |
y |
z |
x |
|
|
|
y |
|
z |
|
||||||||||||
dt |
|
|
|
dt |
|
|
dt |
dt |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Используя в последнем равенстве формулы Пуассона получим формулу, которой устанавливается связь между абсолютной и относительной производными вектора:
du |
|
du |
|
|
. |
(4.3) |
|
u |
|||||||
dt |
dt |
||||||
|
|
|
|
|
32
4.Сложное движение точки
Вэтой формуле – угловая скорость вращения подвижного пространства в неподвижном.
Обратим внимание на два следствия формулы (6.3).
1. Производные вектора в поступательно движущихся одно в другом пространствах одинаковы.
2. Абсолютная производная вектора, постоянного в подвижном пространстве,
du |
|
|
, |
если |
|
const в Axyz . |
(4.4) |
|
u |
u |
|||||||
dt |
||||||||
|
|
|
|
|
|
|
ТЕОРЕМЫ О СЛОЖЕНИИ СКОРОСТЕЙ И УСКОРЕНИЙ
|
Пусть радиус-векторы r |
и |
|||||||||||
|
точки |
М в |
пространствах |
||||||||||
O и |
Axyz |
|
связаны |
равен- |
|||||||||
ством |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
rA . |
(4.5) |
||||||
|
|
|
r |
||||||||||
|
Рассмотрим относитель- |
||||||||||||
ное движение точки. |
|
|
|||||||||||
|
Для |
скорости и ускорения |
|||||||||||
ar |
точки М в пространстве |
и |
|||||||||||
Axyz имеем: |
|
|
|
|
|
|
|
|
|||||
Fig. 6.3 |
|
|
v |
d |
, |
|
(4.6) |
||||||
|
|
|
|||||||||||
|
|
|
r |
|
|
dt |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
a |
|
d 2 |
|
|
d 2v |
|
|
|||||
|
|
|
|
|
|
|
r |
. |
(4.7) |
||||
|
|
|
|
|
|
|
|
||||||
|
r |
dt2 |
|
|
|
dt |
|
|
|||||
|
|
|
|
|
|
|
|
||||||
Переносное движение
Когда точка М совершает переносное движение в неподвижном пространстве, ее радиус-вектором в этом пространстве служит вектор r1 , равный:
r1 rA const в Axyz .
33

4. Сложное движение точки
Поэтому наблюдатель в неподвижном пространстве O для нахождения переносных скорости и ускорения воспользуется равенствами:
v |
|
dr1 |
|
v |
|
|
|
d |
|
|
v |
|
, |
(4.8) |
|
|
A |
|
|
const в Axyz |
A |
||||||||||
e |
|
dt |
|
|
|
dt |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a |
d 2r1 |
|
dvA |
|
(4.9) |
|||||||||
|
|
|
|||||||||||||
|
|
e |
|
dt2 |
|
|
dt |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
Абсолютное движение
v |
d r |
|
d rA |
|
d |
|
d rA |
|
d |
. |
|
|
|
|
|
||||||
a |
dt |
|
dt dt |
dt dt |
|
|||||
|
|
|
||||||||
С учетом равенств (9) и (11) получим |
|
|
|
|
||||||
|
|
|
va vr ve |
(4.10) |
||||||
Теорема 1. Абсолютная скорость точки равна сумме ее относительной и переносной скоростей.
Для абсолютного ускорения получаем
|
|
|
a |
d va |
|
d ve |
|
d vr |
|
d |
v |
|
|
|
d vr |
|
v |
||||||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
||||||||||||||||||
|
|
|
a |
dt |
|
|
dt |
|
dt dt |
|
|
|
|
|
|
dt |
r |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В свою очередь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
d |
v |
|
|
|
d vA |
|
d |
|
|
|||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
dt |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
d v |
A |
|
|
|
|
|
|
d |
|
|
|
|
|
d v |
A |
vr . |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
dt |
|
|
|
|
|
dt |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
||||||||
С учетом равенств (7) и (9) получаем: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
aa ar ae 2 vr . |
|
|||||||||||||||||
2 |
vr aк называется добавочным ускорением или ускорением Ко- |
||||||||||||||||||||||||||||
риолиса.
Теорема 2. (Теорема Кориолиса). Абсолютное ускорение точки равно сумме ее относительного, переносного и добавочного ускорений
34
4. Сложное движение точки
aa ar ae aк . |
(4.11) |
Нахождение ускорения Кориолиса
Добавочное ускорение точки в неподвижном пространстве, которое называется ускорением Кориолиса или поворотным, равно удвоенному векторному произведению угловой скорости вращения подвижного пространства и относительной скорости vr точки
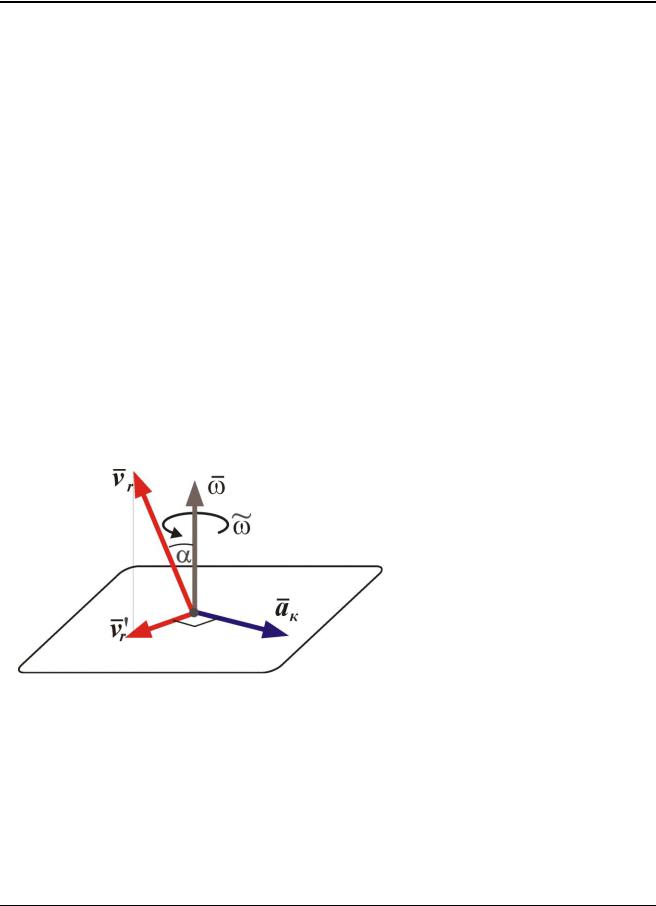
Модуль и направление добавочного ускорения точки часто проще находить, используя правило Н.Е. Жуковского построения векторного произведения.
Модуль добавочного ускорения точки равен удвоенному произведению мо-
дуля угловой скорости |
|
отно- |
подвижного пространства и модуля проекции vr |
||
сительной скорости этой точки на плоскость, перпендикулярную вектору : |
||
ak |
|
|
vr sin . |
|
|
|
|
2 vr , |
vr |
|
|
|
|
||
Направление вектора ak |
|
|
|
° |
|
|
в сторо- |
|
|
|
|
|
|||
получается поворотом на 90 проекции vr |
|||||||
ну вращения подвижного пространства. |
|
|
|
|
|
|
|
|
|
|
Теорема 3. В случае по- |
||||
|
|
|
ступательного движения по- |
||||
|
|
|
движного пространства в не- |
||||
|
|
|
подвижном |
абсолютное |
|||
|
|
|
ускорение точки равно сум- |
||||
|
|
|
ме ее относительного и пе- |
||||
|
|
|
реносного ускорений. |
||||
|
|
|
|
|
aa ar ae . |
||
Рис. 4.4 |
|
|
Утверждение |
теоремы |
|||
|
|
|
очевидно: если |
равна нулю |
|||
угловая скорость подвижного пространства, то обращается в нуль и добавочное ускорение ak точки в неподвижном пространстве.
35

Оглавление
ОГЛАВЛЕНИЕ |
|
ВВЕДЕНИЕ .............................................................................................................. |
1 |
КООРДИНАТЫ И УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОГО ОБЪЕКТА (МО)........................................................ |
1 |
1. Кинематика точки................................................................................................ |
2 |
СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ ................................................................................................................ |
2 |
ЕСТЕСТВЕННЫЕ ОСИ КРИВОЙ................................................................................................................................ |
4 |
СКОРОСТЬ ТОЧКИ. ................................................................................................................................................. |
7 |
УСКОРЕНИЕ ТОЧКИ................................................................................................................................................ |
9 |
КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ТОЧКИ И КРИТЕРИИ ХАРАКТЕРА ДВИЖЕНИЯ ...................................................... |
11 |
2. Простейшие движения твердого тела.............................................................. |
13 |
ОСНОВНЫЕ ТЕОРЕМЫ КИНЕМАТИКИ ТВЕРДОГО ТЕЛА ........................................................................................ |
13 |
ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ................................................................................................. |
14 |
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ........................................................................ |
16 |
ФОРМУЛЫ ПУАССОНА ........................................................................................................................................ |
22 |
3. Плоское движение твердого тела..................................................................... |
23 |
КООРДИНАТЫ И УРАВНЕНИЯ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ............................................................... |
23 |
СКОРОСТИ ТОЧЕК ПЛОСКОЙ ФИГУРЫ .................................................................................................................. |
25 |
МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ ТОЧЕК ФИГУРЫ ............................................................................................. |
26 |
УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ ............................................................................................................... |
29 |
4. Сложное движение точки ................................................................................. |
30 |
АБСОЛЮТНОЕ, ОТНОСИТЕЛЬНОЕ И ПЕРЕНОСНОЕ ДВИЖЕНИЯ ТОЧКИ................................................................. |
30 |
СВЯЗЬ МЕЖДУ ПРОИЗВОДНЫМИ ВЕКТОРА В ДВУХ ПРОСТРАНСТВАХ.................................................................. |
32 |
ТЕОРЕМЫ О СЛОЖЕНИИ СКОРОСТЕЙ И УСКОРЕНИЙ............................................................................................ |
33 |
36
