
КИНЕМАТИКА
.pdf
2. Простейшие движения твердого тела
Тангенс угла наклона полного ускорения к нормали tg 2 .
Рис. 2.7 |
Рис. 2.8 |
|
Из равенства (2.7) видно, что модули ускорений точек тела, вращающегося около неподвижной оси, как и модули их скоростей, пропорциональны расстояниям точек от оси вращения тела.
При решении задач удобно пользоваться следующими зависимостями для скорости и ускорения точки вращающегося тела (рис. 2.8):
|
|
|
|
|
|
|
|
|
|
|
v CM , v CM . |
|
|
(2.8) |
|||||
|
a an a ; |
|
|
|
(2.9) |
||||
a 2CM , a |
|
|
|
|
|
|
|
||
MC; a CM , a |
|
|
|||||||
|
CM . |
||||||||
n |
n |
|
|
|
|
|
|||
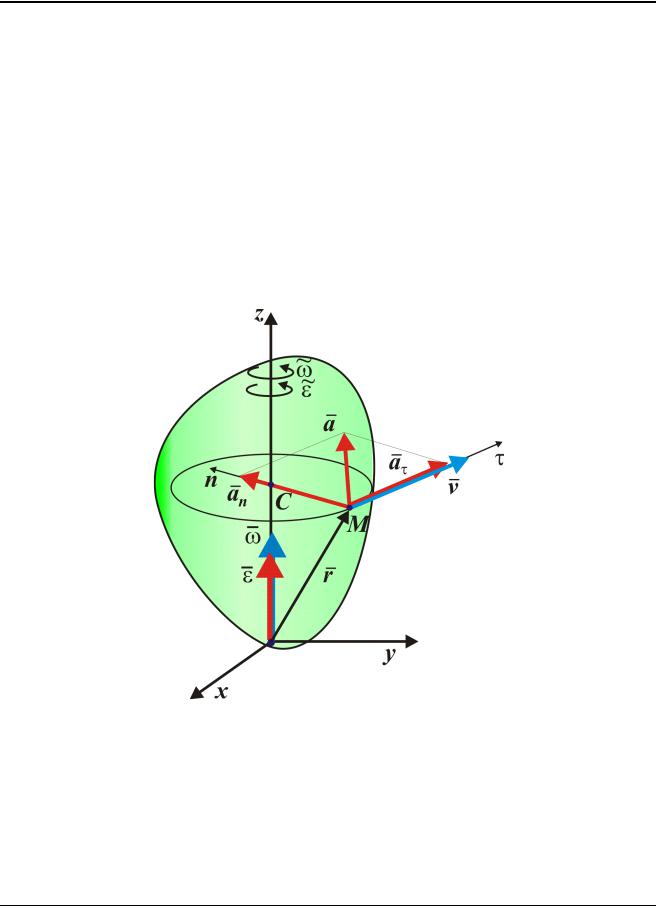
Вектор скорости точки тела, вращающегося вокруг неподвижной оси можно определить как векторное произведение вектора угловой скорости на радиусвектор этой точки относительно некоторого центра на оси вращения (рис. 2.9).
v r . |
(2.10) |
20
2.Простейшие движения твердого тела
Всамом деле, легко проверить, что и модуль и направление векторного произведения (2.10) удовлетворяет зависимостям (2.8).
Равенство(2.10), которое называется формулой Эйлера, описывается поле скоростей точек тела, вращающегося около неподвижной оси. Оно называется ротационным, или Эйлеровым.
Ускорение точки вращающегося тела в векторной форме можно получить дифференцируя по времени зависимость (2.10).
a |
d v |
|
d |
r |
d |
|
r |
d r |
r v . |
|
dt |
dt |
dt |
dt |
|||||||
|
|
|
|
|
||||||
Рис. 2.9
Нетрудно проверить, что
r a – тангенциальное ускорение точки,
v an – нормальное ускорение точки.
21

2. Простейшие движения твердого тела
Производная от вектора постоянной длины
Вектор постоянной длины можно рассматривать как радиус-вектор точки вращающегося тела. Поэтому можно утверждать что
d |
. |
(2.11) |
dt |
Производная от вектора постоянной длины равна векторному произведению угловой скорости на вектор.
ФОРМУЛЫ ПУАССОНА
Воспользуемся формулой (2.11) для нахождений производных ортов i , j ,k подвижных осей Ax , Ay , Az , жестко связанных с телом
Только теперь вектор будем рассматривать как угловую скорость пространства Axyz .
Подставляя в уравнение (2.11) вместо вектор i , получим первую из формул Пуассона
didt i .
Аналогично получаются две другие:
|
|
|
|
|
|
|
|
|
|
|
|
dj |
|
|
|
|
dk |
|
|
||||
|
|
j |
, |
|
|
k |
. |
||||
dt |
|
dt |
|
||||||||
|
|
|
|
|
|
|
|
||||
Здесь – угловая скорость подвижного пространства в неподвижном.
22
3.Плоское движение твердого тела
3.ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
КООРДИНАТЫ И УРАВНЕНИЯ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
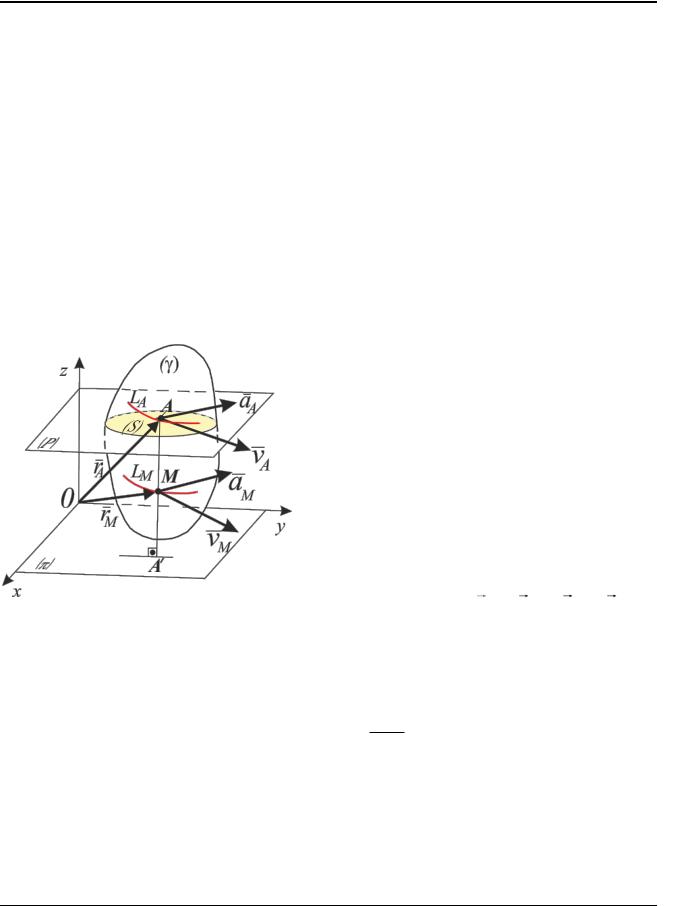
Движение твердого тела в пространстве Оxyz называется плоским (плоскопараллельным), если все его точки движутся в параллельных плоскостях. Любая из них, например плоскость π (рис.3.1), называется направляющей плоскостью или плоскостью движения тела. Расстояния точек тела в плоском движении до направляющей плоскости остаётся
неизменными.
AA const .
Рис. 3.1
такие точки тела. В равенстве
Лемма. Точки тела, расположенные на одном перпендикуляре к направляющей плоскости, движутся одинаково; их траектории – конгруэнтные кривые, скорости и ускорения одинаковы в каждый момент времени.
|
|
|
LA LM , vA vM , aA aM |
|
Доказательство. Пусть А и М – две |
||
|
|
|
|
rM rA AM , |
(3.1) |
||
которым связаны их радиус-векторы, вектор AM постоянен
|
|
|
AM const . |
(3.2) |
|
23
3. Плоское движение твердого тела
Так как траекторией точки служит годограф ее радиус-вектора, то из равенства (3.1) при условии (3.2) следует, что траектория LM точки М может быть
получена сдвигом на вектор AM траектории LA точки А.
LM LA .
Дифференцированием этого же равенства находим:
vM vA , aB aA .
Плоская фигура S сечения тела γ плоскостью
щей плоскости, движется все время в этой плоскости (Р).
Поэтому, при изучении плоского движения твердого тела достаточно иссле-
довать движение плоской фигуры S в ее плоскости Р. |
|
|
|
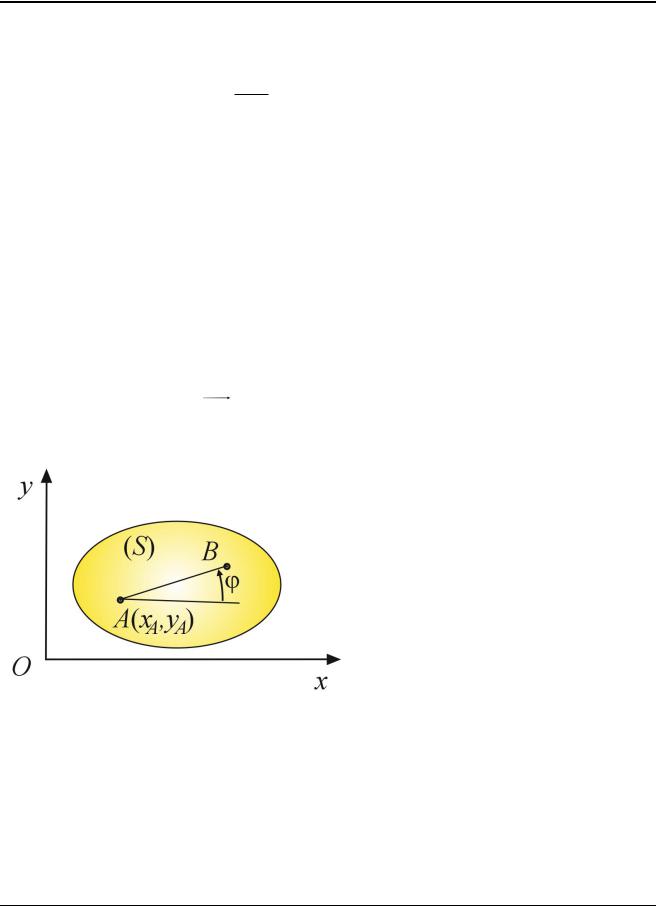
За координаты фигуры S примем координаты |
xA , yA какой-либо точки |
||
A S и угол φ отрезка |
AB S , например, с осью Ох (рис. 3.2). Точку А назо- |
||
вем полюсом фигуры, а угол φ – углом поворота фигуры около полюса. |
|||
|
Зависимости |
координат |
|
|
xA , yA , фигуры S а значит и тела |
||
|
от времени t (3.1) будут уравне- |
||
|
ниями |
плоского |
движения в |
|
плоскости Р. |
|
|
Рис. 3.2
Парциальными движениями фигуры на плоскости
xA x t , |
|
|
|
yA y t , |
(3.3) |
|
|
t .
Oxy являются:
1)xA — поступательное вдоль оси x ;
2)yA — поступательное вдоль оси y ;
3)— вращательное вокруг оси, S , проходящей через полюс A.
24

3. Плоское движение твердого тела
Если два первых поступательных движения заменить одним поступательным, то любое перемещение фигуры можно осуществить последовательностью ее поступательного и вращательного движений. Поступательная часть движения фигуры при перемещении ее из одного положения в другое зависит от выбора полюса, а вращательная часть — не зависит, т.е. одинакова для любого полюса. За положительное направление вращения плоской фигуры примем направление против часовой стрелки.
Угловая скорость фигуры определяется отношением
|
|
d |
. |
|
||
|
k |
(3.4) |
||||
|
|
|||||
|
|
|
dt |
|
||
где k – единичный вектор, направленный перпендикулярно плоской фигуре на наблюдателя (рис. 3.3). Вектор направлен перпендикулярно плоскости фигуры в ту сторону, откуда поворот фигуры на угол d виден против хода часовой стрелки.
Угловое ускорение фигуры определяется производной угловой скоростипо времени:
|
d |
. |
(3.5) |
|
|||
|
d t |
|
|
СКОРОСТИ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
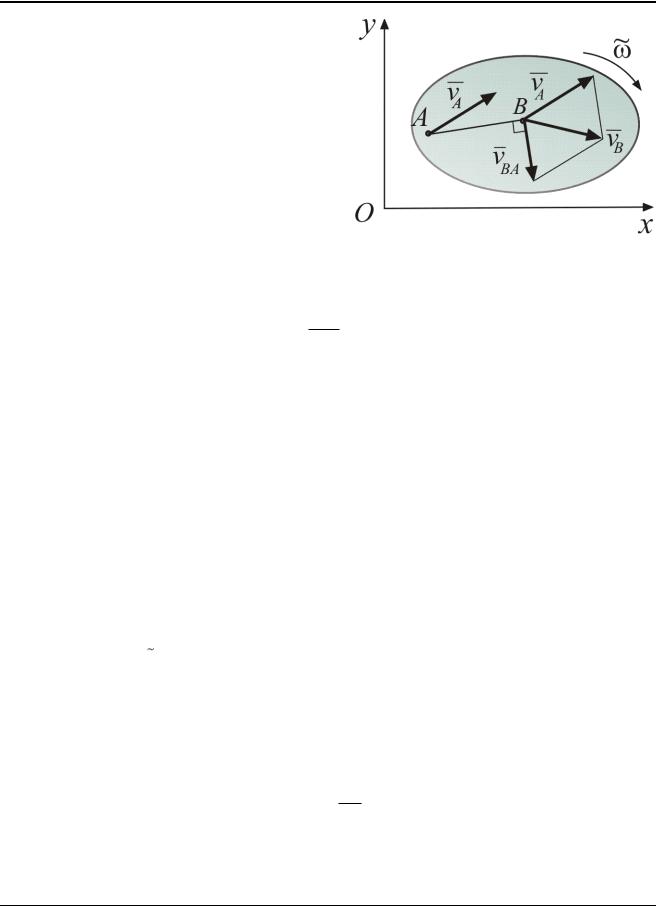
Для нахождения скорости произвольной точки В фигуры воспользуемся теоремой о скоростях точек твердого тела.
Скорость любой точки фигуры равна сумме ее скоростей в каждом из элементарных парциальных движений фигуры:
vB vA vBA .
где vBA скорость точки В в круговом движении около полюса А:
|
|
|
|
vBA AB , |
vBA AB, |
||
где – модуль угловой скорости фигуры.
25
3. Плоское движение твердого тела
Скорость произвольной точки фигуры равна скорости ее полюса, сложенной со скоростью этой точки в круговом движении около полюса.
В задаче скоростей за полюс следует принимать ту точку фигуры, скорость которой известна или достаточно просто находится.
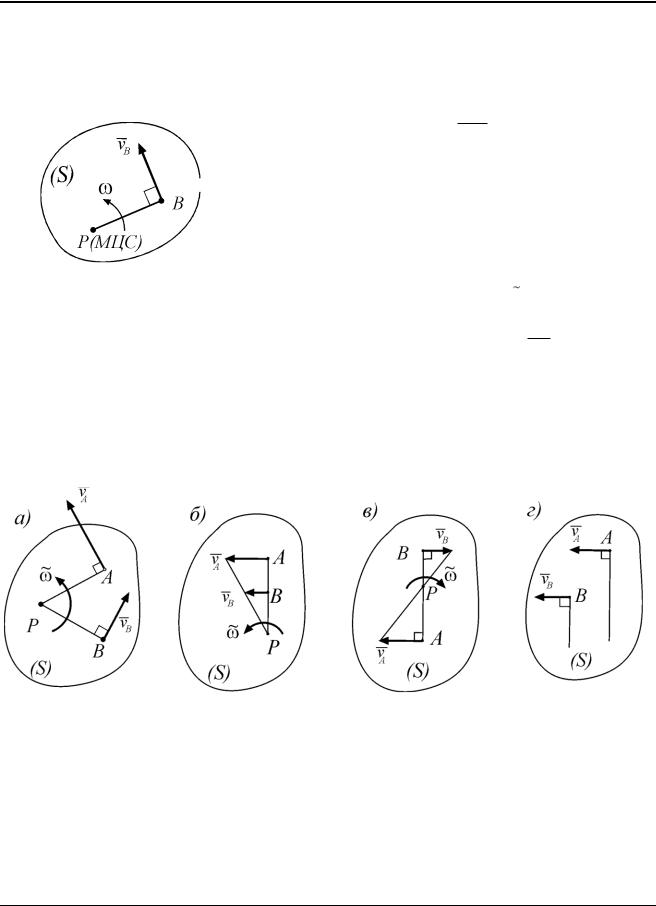
Модуль угловой скорости фигуры Рис. 3.3 находится по формуле
vABBA .
Модуль угловой скорости фигуры равен модулю скорости какой-либо ее точки в круговом движении вокруг полюса, деленному на расстояние от этой точки до полюса.
Алгебраическая угловая скорость ~ фигуры определяется по направлению
скорости vBA .
МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ ТОЧЕК ФИГУРЫ
В каждый момент времени на плоскости движущейся фигуры имеется точка, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей ее точек или МЦС фигуры.
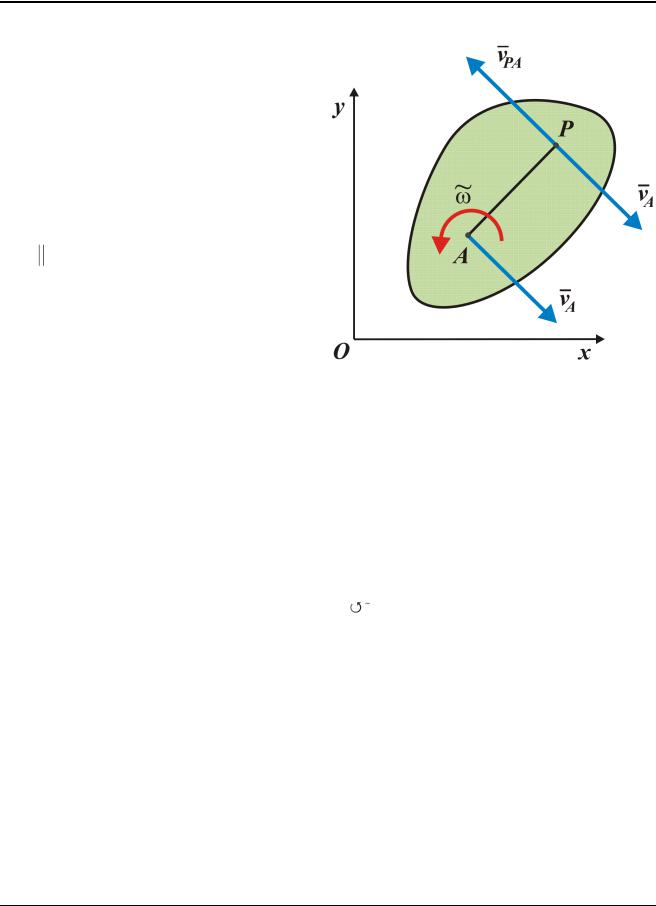
Пусть vA и скорость точки А фигуры и ее алгебраическая угловая ско-
рость в некоторый момент времени (рис. 3.5). На перпендикуляре к скорости vA ,
отклоненном от этого вектора в сторону вращения фигуры, отложим отрезок АР, равный
AP vA .
26
3. Плоское движение твердого тела
Скорость точки Р |
фигуры |
найдем с помощью равенства |
|
vP vA vPA . |
(3.6) |
Скорость точки Р в круговом ее движении около точки А направлена перпендикулярно отрезку АР в сто-
рону |
вращения фигуры и |
поэтому |
vPA |
vA Модуль этой скорости |
|
|
vPA AP vA . |
|
Таким образом, |
|
|
|
vPA vA |
Рис. 3.4 |
и в соответствии с равенством (3.6), находим
vP 0.
Следовательно, в рассматриваемый момент времени точка Р фигуры является ее MЦC.
Примем за полюс фигуры точку Р – ее МЦС. Тогда для скорости произвольной точки В фигуры получим
|
|
|
|
|
|
|
|
|
|
|
|
|
PB |
|
|||
|
|
|
|
|
||||
|
|
v |
B |
|
|
|||
vB PB |
|
|
|
B S , |
||||
|
|
v |
B |
BP |
|
|||
|
|
|
|
|
|
|
|
|
где точка Р – мгновенный центр скоростей фигуры (рис. 3.4). Таким образом:
Скорость произвольной точки фигуры равна её скорости во вращательном движении фигуры около мгновенного центра скоростей (МЦС).
Движение фигуры в каждый момент времени является мгновенновращательным около оси, проходящей через МЦС перпендикулярно плоскости фигуры.
27
3. Плоское движение твердого тела
Модуль угловой скорости фигуры равен модулю скорости какой-либо ее точки, деленному на расстоянии от этой точки до МЦС.
BPvB .
Алгебраическая угловая скорость ~ фигу-
ры определяется по направлению скорости vB
Два правила нахождения МЦС фигуры:
1) Известны скорость vB точки В и алгеб-
раическая угловая скорость фигуры. МЦС
Рис. 3.5
находится на расстоянии BP vB от точки В
на перпендикуляре к скорости vB этой точки, отклоненном от ее скорости на прямой угол в сторону вращения фигуры (рис. 3.5);
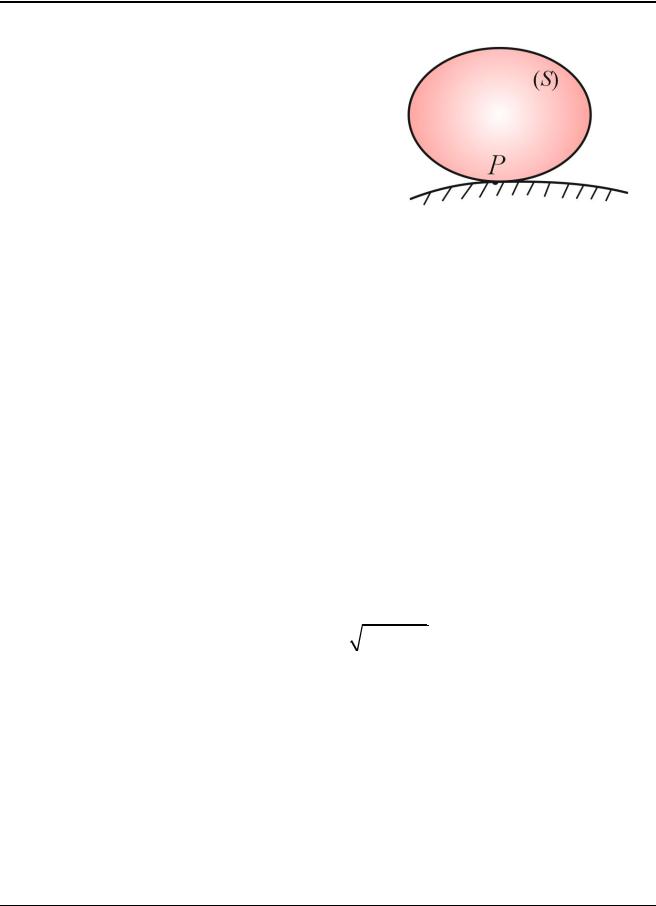
2) Известны скорости vA , vB двух точек A и B . МЦС находится в точке пересечения перпендикуляров к скоростям двух точек фигуры (рис. 3.6а).
Рис. 3.6
В случаях, когда перпендикуляры к скорости совпадают, нахождение МЦС фигуры показано на рис. 3.6б, в. Если же они параллельны (рис. 3.6г) – пересекаются в бесконечно удаленной точке, МЦС фигуры устремляется в бесконечность и ее движение является мгновенно-поступательным (угловая скорость
28
3. Плоское движение твердого тела
~ ). Его можно рассматривать как
0
мгновенно-вращательное около МЦС, находящегося в бесконечности.
Иногда сразу можно назвать точку |
|
фигуры, скорость которой равна нулю. |
|
Например, при качении без скольжения |
|
фигуры по неподвижной кривой ее МЦС |
|
находится в точке контакта (соприкосно- |
|
вения) фигуры с кривой (рис. З.7). |
Рис. З.7 |
|
УСКОРЕНИЯ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
Ускорение произвольной точки фигуры равно ускорению полюса фигуры, сложенному с ускорением этой точки в круговом ее движении около полюса
aB aA aBA .
Заменяя здесь два последних слагаемых ускорением aBA точки В в круго-
вом движении около, полюса А
aBA aBAn aBA ,
получим
aB aA aBAn aBA .
Модуль ускорения
aBA AB 
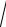 2 4 .
2 4 .
29
