
МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ
.pdf
Ранее мы говорили о важнейших требованиях, предъявляемых к любой математической теории: это непротиворечивость, полнота, разрешимость. Выясним, удовлетворяет ли этим требованиям построенное нами И.В.
Воснове формализованного И.В. лежат понятия, представляющие собой некие абстрактные, лишенные смысла знаки и формальные действия с ними: алфавит, формула, аксиома, правило вывода, доказательство, теорема.
Вто же время А.В., изученная ранее, пронизана содержательным смыслом: за каждой пропозициональной переменной стоит конкретное высказывание, каждая формула может превращаться в конкретное составное высказывание, некоторые формулы могут превращаться только в истинные высказывания (тавтологии) и т.д.
Возникает вопрос: существует ли связь (и если существует, то какова она) между формализованным ИВ и содержательной АВ? Установить искомую связь призвана теорема о полноте ИВ, которая будет доказана позднее. Оказывается, ИВ построено таким образом, что всякая его теорема является тавтологией (т.и.ф.) АВ, и обратно, для всякой тавтологии АВ можно построить ее вывод из аксиом ИВ, т.е. доказать, что она является теоремой ИВ. Т.о. теорема полноты связывает абстрактную аксиоматическую теорию исчисления высказываний и содержательную АВ, теорию с практикой.
Интерпретация ИВ. Непротиворечивость ИВ. (Связь ИВ с АВ)
Пропозициональные переменные будем истолковывать как высказывания, которые принимают значения из множества {0, 1}, логические связки , будем истолковывать как операции над высказываниями, определяемые теми же таблицами истинности, что и А В, А .
Опр. Формула ИВ называется тавтологией или т.и.ф., если на любом наборе значений переменных она принимает значение 1 (истина).
Лемма 1. Все аксиомы ИВ являются тавтологиями.
41

Проверим аксиому А1: А (В А). Построим таблицу истинности:
А |
(В |
|
А) |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Также проверяются остальные аксиомы.
Лемма 2. Правило вывода МР сохраняет тавтологичность формулы, т.е., если А и А В – тавтологии, то В – тавтология.
Доказательство (методом от противного):
Допустим, что В не является тавтологией, т.е. существует набор значений переменных, на котором значение формулы В равно 0 (ложь), т.к. А – тавтология, то импликация А В на наборе (1,0) ложна, т.к. В – ложна по допущению, что противоречит условию А В – тавтология. Следовательно, формула В – тавтология.
Отсюда следуют теоремы:
Т1. Если формула ИВ выводима, то она является тавтологией.
├А  А – Т.И.Ф.
А – Т.И.Ф.
Доказательство проведем м.м.и.
Дано: формула А – выводима из аксиом в ИВ, т.е. существует ее вывод:
F1, F2, …, Fn=А – вывод А.
Покажем что любая формула вывода является ТИФ. Индукцию будем проводить по длине вывода формулы А.
I.Построение базиса. Пусть n =1.
F1 – аксиома ( по лемме 1 – она тавтология).
II.Индукционный шаг. Пусть доказано, что для n N, 1<n<k Fn является тавтологией.
Докажем, что при n=k – Fk тавтология.
Для формулы Fk возможны случаи: |
|
|
|
а) Fk – аксиома, |
Fk – тавтология по лемме 1. |
|
|
б) Fk получена по правилу МР из Fi и Fj (i, j<k) |
Fk |
– |
|
тавтология по лемме 2. |
|
|
|
42

Следовательно, теорема справедлива n N.
Следствие: Если формула не тавтология, то она в ИВ не выводима.
Опр. ИВ называется непротиворечивым, если не существует формулы А такой, что одновременно в этом ИВ выводима она сама и ее отрицание, т.е. ├А и
├ А .
Замечание: Требование непротиворечивости – важнейшее требование к математической теории.
Т2. Исчисление высказываний непротиворечиво. Доказательство: Допустим противное. Пусть ИВ – проти-
воречиво, т.е. существует формула А такая, что ├А и ├ А . Т.к.
├А, то по Т1 она является тавтологией, но тогда А тавтологией не является и поэтому она выводимой быть не может. Приходим к противоречию. Следовательно ИВ непротиворечиво.
Для доказательства теоремы, обратной к Т1 потребуется лемма:
Лемма о полноте ИВ
Введем обозначения:
F(x1, x2, …, xn) – формула ИВ,
x1, x2, …, xn – список попарно различных переменных, среди которых есть все переменные, входящие в формулу F.
Пусть =< 1, 2, …, n> – упорядоченный набор длины n
из 0 и 1: i {0, 1}, i 1,n.
|
xi , если i 1; |
|
||||
xi |
|
|
|
|
|
|
|
|
|
||||
|
xi , если i 0. |
|
||||
F |
F , если значение F |
на наборе 1; |
||||
|
|
|
на наборе 0. |
|||
|
||||||
|
F , если значение F |
|||||
Пример: Пусть F=x1 x3; = <0, 1, 1>, тогда x1 x1 , x2 x2 , x3 x3 .
F F x1 x3 , т.к. 0 1=1.
Если = <1, 0, 0>, то x1 x1 , x2 x2 , x3 x3 . F F x1 x3 , т.к. 1 0=0.
43

Лемма (о выводимости).
Для любой формулы F(x1, x2, …, xn) и любого набора справедлива выводимость: x1 , х2 ,…, хn ├F (x1, x2, …, xn).
Дано: Г={x1 , х2 , …хn }. Требуется доказать, что Г├F .
Доказательство проведем м.м.и. по длине формулы F (числу логических связок k, входящих в запись формулы).
I.Базис: k=0; F=xi.
Нужно доказать: x1 , х2 , … xi , …, хn ├F =xi – следует по свойству 1 выводимости из гипотез.
II.Пусть для любой формулы длины 0<k<s лемма вы-
полняется. Рассмотрим формулу длины k=s. Возможны случаи:
1)F F1;
2)F F1 F2 , F1 и F2 имеют длину меньше, чем s и для
них утверждение леммы выполняется, т.е. Г├F1 , Г├F2 . Требуется доказать: Г├F .
1) Рассмотрим 1–й случай: F F . Дано: Г├F1 .
Доказать: Г├F . Возможны 2 подслучая:
№ |
Знач. F1 |
F1 |
Знач. F |
F |
||||
а) |
0 |
|
|
|
1 |
F |
||
F1 |
||||||||
б) |
1 |
F1 |
0 |
|
|
|
||
F |
||||||||
1 подслучай: а) Дано: Г├F1 = F1. Доказать: Г├F =F= F1.
То, что требуется доказать – дано.
2 подслучай: б) Значение F1 на равно 1. Дано: Г├F1 =F1.
Доказать: Г├F = F (F F1).
Требуемое следует по закону введения двойного отрица-
ния.
2) Рассмотрим 2–й случай: F F1 F2 .
44
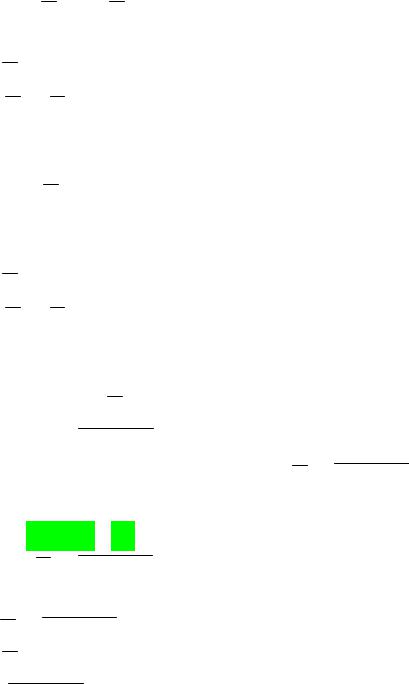
По индукционному предположению лемма считается верной для формул F1 и F2. Здесь возможны 4 подслучая:
№ |
Знач. F1 |
Знач. F2 |
F1 |
F2 |
Знач. F |
F |
|||||||||
а) |
0 |
0 |
|
|
|
|
|
|
|
|
1 |
F |
|||
|
F1 |
F2 |
|||||||||||||
б) |
0 |
1 |
|
|
|
|
F2 |
1 |
F |
||||||
F1 |
|||||||||||||||
в) |
1 |
0 |
F1 |
|
|
|
|
0 |
|
|
|
||||
F2 |
|||||||||||||||
|
F |
||||||||||||||
г) |
1 |
1 |
F1 |
F2 |
1 |
F |
|||||||||
В каждом из подслучаев запишем, что дано и что требуется доказать.
а) Дано: Г├ F1, Г├ F2 .
Доказать: Г├F1 F2.
1)Г├ F1……………………дано
2)Г , F2 ├ F1………………из 1) по 2
3)Г, F1├F2………………...из 2) по О.К.
4)Г├F1 F2………………..из по ТД.
б) Дано: Г├ F1, Г├F2.
Доказать: Г├F1 F2.
Доказательство совпадает с предыдущим случаем.
1)Г├ F1……………………дано
2)Г , F2 ├ F1………………из 1) по 2
3)Г, F1├F2………………...из 2) по О.К.
4)Г├F1 F2………………..из по ТД.
в) Дано: Г├F1, Г├ F2 .
Доказать: Г├F1 F2 .
Иначе, требуется доказать: Г , F1 , F2 ├ F1 F2 . Доказательство:
1)Г, F1, F1 F2├F2…………..МР к списку гипотез
2)Г , F1 , F2 ├ F1 F2 …………из 1) по П.К.
3)Г├F1………………………..дано
4)Г , F2 ├ F1 F2 ……………..из 3), 4) по 3
5)Г├ F2 ………………………..дано
6)Г ├ F1 F2 ………………….из 4), 5) по 3 .
45

г) Дано: Г├F1, Г├F2.
Доказать: Г├F1 F2.
1)Г├F2………………………….дано
2)Г, F1├F2………………………из 1) по 2
3)Г├F1 F2……………………...из 2) по ТД.
Т.о., лемма справедлива для любой формулы F.
Полнота ИВ
Опр. ИВ называется полным, если в нем выводима любая тавтология (ТИФ).
Т. (о полноте) ИВ полно, т.е. если формула является тавтологией, то она выводима в ИВ.
Доказательство:
Пусть А – ТИФ, тогда А =А для любого набора . Применим лемму о полноте
x1 , х2 , …хn ├А =А.
Пусть – набор, имеющий вид =< 1, 2, …, n-1, 1>. Для этого набора получаем:
x1 , х2 , …хn-1 , хn├А………………..(1).
Возьмем другой набор =< 1, 2, …, n-1, 0>. Для него имеем по лемме о полноте:
x1 , х2 , …хn-1 , xn ├А…………………(2).
К соотношениям (1) и (2) применим правило удаления дизъюнкции:
x1 , х2 , …хn-1 , xn xn ├А, расшифруем дизъюнкцию:
xn xn
├xn xn – пример 1.
Выводимые формулы из списка гипотез можно исключать
(элеменировать) по свойству 3 : x1 , х2 , …хn-1 ├А.
Аналогично удаляются остальные гипотезы. Через конечное число шагов получим: х1├А
x1├А, применяем удаление дизъюнк-
ции: x1 x1├А x1 x1├А ├А.
Пример: Пусть А – тавтология, содержащая 2 переменные.
46
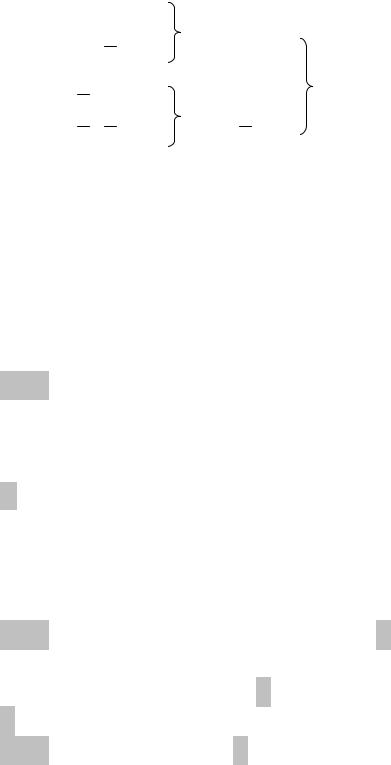
По лемме справедливы выводимости: 1) x1,x2 ├А
2) x1,x2├А
3) x1,x2├А
4) x1,x2├А x1├А ├А.
Следствие: Формула выводима в ИВ , когда она является тавтологией.
Это вытекает из теоремы о полноте и Т1 из предыдущего пункта.
Свойство полноты говорит о том, что система аксиом подобрана удачно. Выбранные аксиомы оказываются независимыми, т.к. ни одну из них нельзя вывести из других.
Разрешимость И.В.
Опр. ИВ называется разрешимым, если существует алгоритм (метод), позволяющий по любой формуле определить, выводима она этом исчислении или нет и ИВ неразрешимо в противном случае.
Т. ИВ (построенное нами) разрешимо.
Разрешающий алгоритм представляет собой построение таблицы истинности, если формула тождественно истинная, то она выводима.
Независимость системы аксиом
Опр. Аксиома А из системы аксиом называется независящей от остальных аксиом этой системы, если ее нельзя вывести (доказать) из множества \{A} всех остальных аксиом системы, кроме аксиомы А.
Опр. Система аксиом называется независимой, если каждая ее аксиома не зависит от остальных.
Из определения следует, как нужно доказывать независимость той или иной аксиомы от остальных аксиом данной системы. Нужно построить модель, в которой выполнялись бы все аксиомы данной системы, кроме той, независимость которой устанавливается.
47
|
|
Лемма 1. Аксиома (А1) не зависит от аксиом (А2) и (А3) |
|||||||
формализованного ИВ. |
|
|
|
|
|||||
|
|
Доказательство. Рассмотрим трехэлементное множество |
|||||||
М={0, 1, 2} и введем на нем 2 операции: унарную, сопостав- |
|||||||||
ляющую каждому элементу А М, элемент, обозначаемый А и |
|||||||||
бинарную, сопоставляющую каждой паре А и В элементов из |
|||||||||
М элемент из М, обозначаемый А В по правилам, определяе- |
|||||||||
мым таблицами: |
|
|
|
|
|
||||
А А |
А В А В |
|
|
|
|
||||
0 |
1 |
|
0 |
0 |
0 |
|
|
|
|
1 |
1 |
|
0 |
1 |
2 |
|
|
|
|
2 |
0 |
|
0 |
2 |
2 |
|
|
|
|
|
|
|
1 |
0 |
2 |
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
1 |
2 |
0 |
|
|
|
|
|
|
|
2 |
0 |
0 |
|
|
|
|
|
|
|
2 |
1 |
0 |
|
|
|
|
|
|
|
2 |
2 |
0 |
|
|
|
|
|
|
Если переменным, входящим в формулу ИВ придать не- |
|||||||
которые значения из М, то согласно введенным правилам сама |
|||||||||
формула примет значение из М. Формулу, всегда принимаю- |
|||||||||
щую значение 0, назовем выделенной. |
|
|
|||||||
|
|
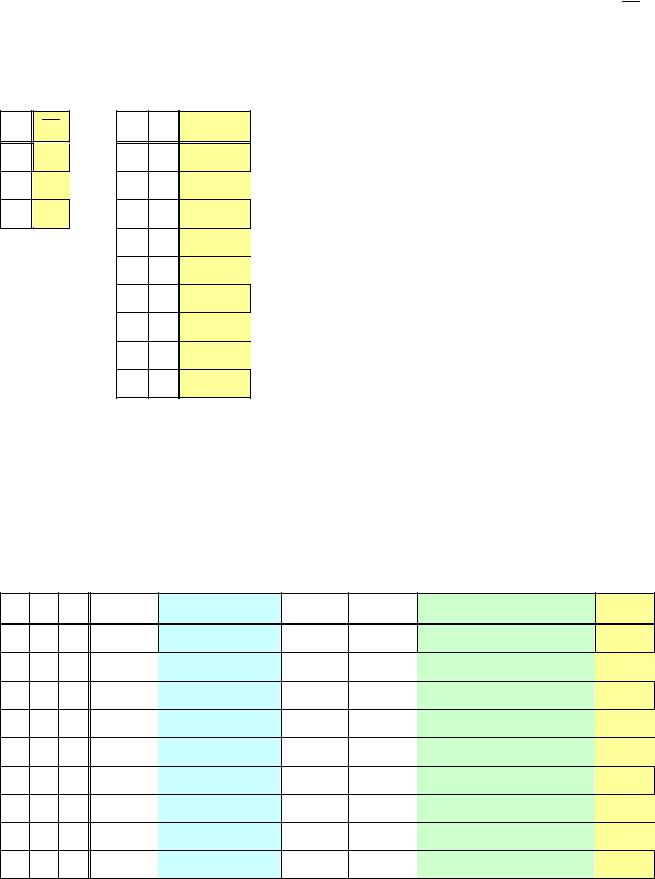
Покажем, что всякая формула, получающаяся по схеме |
|||||||
аксиом (А2) является выделенной. Для этого составим таблицу |
|||||||||
значений формулы (А2): |
А (В С) ((А В) (А С)) |
|
|||||||
А В С В С А (В С) |
А В А С (А В) (А С) (А2) |
||||||||
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
|
2 |
0 |
2 |
2 |
0 |
0 |
0 |
2 |
2 |
|
2 |
0 |
2 |
2 |
0 |
0 |
1 |
0 |
2 |
|
2 |
2 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
|
2 |
2 |
2 |
0 |
0 |
0 |
1 |
2 |
0 |
|
0 |
2 |
2 |
0 |
0 |
0 |
2 |
0 |
0 |
|
0 |
2 |
0 |
0 |
0 |
0 |
2 |
1 |
0 |
|
0 |
2 |
2 |
0 |
0 |
0 |
2 |
2 |
0 |
|
0 |
2 |
2 |
0 |
0 |
|
|
|
|
|
|
|
|
|
48 |
1 |
0 |
0 |
0 |
2 |
2 |
2 |
0 |
0 |
1 |
0 |
1 |
2 |
0 |
2 |
2 |
0 |
0 |
1 |
0 |
2 |
2 |
0 |
2 |
0 |
0 |
0 |
1 |
1 |
0 |
2 |
0 |
2 |
2 |
0 |
0 |
1 |
1 |
1 |
2 |
0 |
2 |
2 |
0 |
0 |
1 |
1 |
2 |
0 |
2 |
2 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
2 |
0 |
2 |
2 |
0 |
1 |
2 |
1 |
0 |
2 |
0 |
2 |
2 |
0 |
1 |
2 |
2 |
0 |
2 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
Покажем, что всякая формула, получающаяся по схеме
аксиом (А3), также является выделенной: |
||||||||||||||||
А |
В |
|
|
|
|
|
|
|
|
|
|
|
|
А В |
(А3) |
|
В |
|
|
А |
|
|
В |
А |
|
||||||||
0 |
0 |
1 |
|
1 |
|
2 |
|
|
|
0 |
0 |
|
||||
0 |
1 |
1 |
|
1 |
|
2 |
|
|
|
2 |
0 |
|
||||
0 |
2 |
0 |
|
1 |
|
2 |
|
|
|
2 |
0 |
|
||||
1 |
0 |
1 |
|
1 |
|
2 |
|
|
|
2 |
0 |
|
||||
1 |
1 |
1 |
|
1 |
|
2 |
|
|
|
2 |
0 |
|
||||
1 |
2 |
0 |
|
1 |
|
2 |
|
|
|
0 |
0 |
|
||||
2 |
0 |
1 |
|
0 |
|
2 |
|
|
|
0 |
0 |
|
||||
2 |
1 |
1 |
|
0 |
|
2 |
|
|
|
0 |
0 |
|
||||
2 |
2 |
0 |
|
0 |
|
0 |
|
|
|
0 |
0 |
|
||||
В третьих покажем, что правило вывода МР сохраняет свойство выделенности. Это видно из таблицы, определяющей операцию . Формулы А и А В принимают одновременно
49
значение 0 только в первой строке, но в этой строке формула В также принимает значение 0.
Т.о., всякая формула, выводимая из аксиом (А2) и (А3) с помощью правила вывода МР является выделенной.
Докажем, что формула (А1) не является выделенной, т.е. ее нельзя вывести из (А2), (А3) с помощью правила МР.
Пусть А=1, В=2:
А (В А)=1 (2 1)=1 0=2 0.
Модель построена. (А1) не зависит от (А2) и (А3). Независимость остальных аксиом доказывается анало-
гично.
50
