6. Теоремы о непрерывных ф-ях.

Т 1. Если y=f(x) и y=g(x) непрерывны в т. x ₀ , то в этой т-ке непрерывны также f(x) ±g(x), f(x)*g(x), f(x)/g(x),(g(x₀) ≠0)

Т 2. Сложная ф-ция, составленная из конечного числа непрерывных ф-ций непрерывна.

Т 3. Ф-я обратная к непрерывной и монотонной ф-ции непрерывна.

Вывод: Все элементарные ф-ции непрерывны в областях, где они определены

Св-ва ф-ций непрерывных на отрезке

Т 1. Если ф-ция y=f(x) непрерывна на отрезке [а,b], то, по крайней мере, в одной т-ке этого отрезка она достигает наибольшее значение и, по крайней мере, в одной наименьшего, т.е

Ė x₁€[a,b],что f(x₁) ≥f(x), ¥ x€[a,b];

Ė x₂€[a,b],что f(x₂)≤ f(x), ¥ x€[a,b];

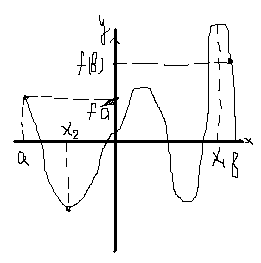
Т 2. Если f(x) непрерывна на [а,b], то она принимает все промежуточные значения между ее значениями на концах, т.е если f(a) ≠f(b),f(a)=A,f(b)=B

Пусть A<C<B,то Ė c€ [а,b], что f(c)=c

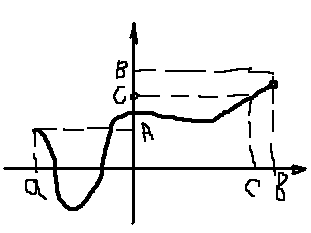
Т 3. Если f(x) непрерывна на [а,b] и f(a) и f(b) разных знаков, то Ė c€ [а,b], что f(c)=0

Дифференциальное исчисление одной переменной.

y=f(x), х €D(f), х+∆x €D(f)c→y-∆y=f(x+∆x)-f(x)

Опр. lim(∆x→0) ∆y/∆x наз производной данной ф-ции , (обозначается f'(x), y'_x, dy/dx, df(x)/dx)

y'=lim(∆x→0) ∆y/∆x

y'=lim(∆x→0) (f(x+∆x)-f(x))/ ∆x

7. Определение производной, её физический и геометрический смысл. Связь дифференцируемости и непрерывности.

Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется какпределотношения приращения функции к приращению ееаргументапри стремлении приращения аргумента кнулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называетсядифференци́рованием.

y=f(x), х €D(f), х+∆x €D(f) ∆y=f(x+∆x)-f(x)

Опр. lim(∆x→0) ∆y/∆x наз производной данной ф-ции, (обозначается f'(x), y'_x, dy/dx, df(x)/dx)

y'=lim(∆x→0) ∆y/∆x

y'=lim(∆x→0) (f(x+∆x)-f(x))/ ∆x

Физический смысл производной

y=f(x) определяет скорость изменения ф-ции в момент х

Геометрический смысл

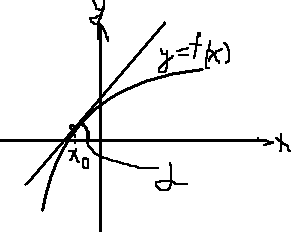
f(x )=tg – угловой коэффициент касательной

Дифференцируемость ф-ции. Связь диффер-ти и непрерывности

Производная f'(x₀) функции f в точке x₀, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x₀ тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в x₀ функции f в окрестности U(x₀) справедливо представление

f(x) = f(x₀) + f'(x₀)(x − x₀) + o(x − x₀) при

По опр y'=lim(∆x→0) ∆y/∆x

Опр. Ф-я y=f(x) наз дифференцируемой в т х, если в этой т-ке существует производная в этой точке.

Ф-ция наз диффер-емой на отрезке [а,b], если она диф-ма в каждой т-ке этого отрезка.

Теорема (связь между диф-тью. и непрерывностью в т.)

Если ф-я диф-ма в т.х , то она непрерывна в этой точке. Обратное неверно!