1. Понятие функции. Способы задания, свойства, классификация функций.

Определение: если одному значению независимой переменной x соответствует одно (много) значений y, то y назыв однозначной (многозначной) функцией аргумента x и обозн y=f(x)

Определение: множество значений аргумента x, для которых функция существует, определена, назыв областью определения функции. D(f)

Определение: множество значений переменной y, соответствующих значений x из области определения, назыв областью значения ф-ции. E(f)

Для нахождения нулей функции нужно решить уравнение f (x) = 0, а для нахождения промежутков знакопостоянства нужно решить неравенства f (x) > 0 и f (x) < 0.

Если на некотором промежутке функция непрерывна и не имеет корней, то она сохраняет знак на этом промежутке.

Определение: ф-ция f(x) называется возрастающей, если большему значению аргумента соответствует большее значение ф-ции, т.е. для x1<x2: f(x1)<f(x2)

Определение: ф-ция f(x) назыв убывающей, если большему значению аргумента соответствует меньшее значение ф-ции, т.е. для x1<x2: f(x1)>f(x2)

Определение: ф-ция f(x) называется чётной, если выполняется f(-x)= f(x)

Ф-ция назыв нечётной, если выполняется

f(-x)= -f(x)

Определение: ф-ция y=f(x) назыв. периодической с периодом Т, еси выполняется соотношение f(x+T)=f(x) основные элементарные ф-ции: y=xⁿ, y=aⁿ, y=log_ax, y=sinx, y=arcsinx,…

Определение: если ф-ция задана звеньями элементарных ф-ций на определённых интервалах, назыв. сложной ф-цией.

Определние: ф-ция x=φ(y) назыв. обратной для ф-ции y=f(x), если первая ф-ция будучи подставлена во вторую, превращает её в тождество: y=f[φ(y)]

2. Числовые последовательности. Предел последовательности. Предел функции.

Определение: Числовой последовательностью назыв множество чисел, пронумерованных с помощью натуральных чисел и расположенных в порядке возрастания их номеров.

у1, у2, …, уn={yn}→yn=f(n), где у1, у2 –члены, yn=f(n) –общий член последов.

Определение: Число а назыв пределом последов, если >0, сколь угодно малого, что для всехn> N(), выполняется, при этом

=a, (a-ε;a+ε) - окрестность

Геометрическая интерпретация

y=f(x) – ф-ция, х - аргумент ф-ции, х→а, f(x) →А, А предел ф-ции

Определение: числа А назыв. пределом ф-ции f(x) при х→а, если >0, сколь угодно малого,>0, что для всехx, для которых выполняется условие <, имеет место<=A

Замечание: 1) х→а как угодно; 2) f(x) в точке а может быть и не определена.

Определение: числа А назыв. пределом ф-ции f(x) при х→∞, если >0, сколь угодно малого, , что для всехx,|x|>N , выполняется.<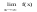=A

Теорема: Любая функция, имеющая предел, является ограниченной.

3. Теоремы о пределах. Односторонние пределы.

Теорема 1: Пусть lim{x→a}f(x)=А и lim{x→a}g(x)=В, тогда 1)lim{x→a}(f(x)+g(x)) = А+В; 2)lim{x→a}(f(x)*g(x)) = А*В; 3)lim{x→a}(f(x)/g(x)) =А/В

Теорема 2: lim f1(x)= А1 lim f2(x) = А2, f1(x)<=f2(x), xD(f) => A1<A2

Теорема 3: lim f1(x)=А, lim f2(x) = А, f1(x)<f(x)<f2(x) => lim f(x) =A

Определение: если при вычислении предела lim{x→a}f(x) при х→а, Х остаётся всё время меньше (больше) а, то предел называется левым(правым) – оба односторонние.

Замечание: 1) Если сущ-ют и равны м/у собой односторонние пределы, то они равны пределу f(x), при х→а. 2) Если существует предел данной функции, то существует и его односторонние пределы.