V. Малые колебания механических систем §17. Свободные одномерные колебания консервативной системы

 Литература: [8] (§ 13).

 Некоторые важные положения

 Свободные одномерные колебания консервативной системы возможны вблизи положения равновесия, соответствующего минимуму потенциальной функции U = U(q) как функции обобщенной координаты q.

 При достаточно малых отклонениях x = q – q₀ от положения равновесия лагранжиан системы можно представить в виде:

L = –. (17.1)

Кинематический параметр m вычисляется следующим образом:

m = =. (17.2)

Динамический параметр k, или коэффициент квазиупругой силы, определяется так:

q = q₀

k =(17.3)

 Лагранжиан (17.1) приводит к динамическому уравнению

+²x = 0, (17.4)

где  = . (17.5)

Этому уравнению удовлетворяют функции, описывающие гармонические колебания:

x = a cos( t + ₀) . (17.6)

Так что в системе с лагранжианом (17.1) реализуются свободные линейные гармонические колебания. Поэтому такую систему называют линейным гармоническим осциллятором.

 Энергия E линейного гармонического осциллятора связана с амплитудой a соотношением

E = m ² a² / 2 . (17.7)

? Задания и контрольные вопросы

1. Расскажите о колебаниях, колебательных движениях и механических колебаниях.

2. При каких условиях возможны свободные одномерные механические колебания?

3. При каких условиях колебания считаются малыми?

4. Каковы особенности малых свободных колебаний консервативной системы?

5*. Выведите формулу (17.1).

6. Расскажите, как находится период малых колебаний консервативной системы.

7. Расскажите, как определяются амплитуда и начальная фаза колебаний гармонического осциллятора.

§18. Вынужденные одномерные колебания при наличии диссипативных сил

 Литература: [3] (§§ 39 – 41), [8] (§§ 25, 26).

 Некоторые важные положения

 Рассматривается система с одной степенью свободы, описываемая лагранжианом (17.1). В системе имеется диссипативная сила (сила сопротивления движению), а также периодически изменяющаяся с циклической частотой  внешняя сила. Диссипативная сила f_Т выражается формулой

f_Т = –  , (18.1)

в которой  > 0 – коэффициент сопротивления. Внешнюю периодически изменяющуюся силу f_В удобно представить в комплексном виде:

f_В = f exp(i  t) . (18.2)

Физический смысл, естественно, имеет действительная часть комплексной величины f_B.

Уравнение Лагранжа рассматриваемой системы записывается так:

+ 2  + ₀² x = exp(i  t), (18.3)

где  =–коэффициент затухания.

 Общее решение уравнения (18.3) имеет вид:

x = x_C(t) + x_В(t) . (18.4)

Первое слагаемое описывает свободное движение , то есть такое, которое происходило бы в замкнутой системе.

Второе слагаемое существенно зависит от внешних сил. Ему соответствуют вынужденные колебания.

 Свободное движение при достаточно малой величине  представляет собой затухающие колебания:

x_C(t) = a exp(– t) cos( t) . (18.5)

Здесь  = (18.6)

– циклическая частота свободных колебаний, а ₀ = –собственная частота осциллятора.

Если  > ₀, то функция x_C(t) существенно отличается от (18.5): вместо колебаний происходит апериодическое затухание, величина x_C(t)  0 при t  .

Из (18.4) следует, что при t   функция x(t)  x_В(t), то есть устанавливаются вынужденные колебания.

 Вынужденные колебания под действием гармонически изменяющейся внешней силы (18.2) представляют собой гармонические колебания с частотой этой силы:

x_В(t) = b cos( t + ) , (18.7)

где b = 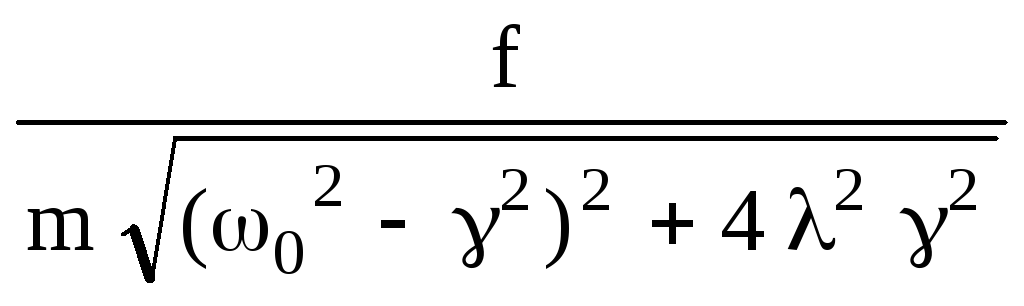, tg = . (18.8)

Амплитуда b вынужденных колебаний существенно зависит от соотношения частот  и ₀. Эта зависимость представлена на рисунке 19.

При  = _Р = (18.9)

амплитуда b достигает максимального значения

b_m = . (18.10)

Явление резкого возрастания амплитуды вынужденных колебаний вблизи _Р носит название амплитудного резонанса.

 Амплитуда колебаний рассматриваемого осциллятора не изменяется с течением времени, если энергия, затрачиваемая системой на преодоление сил трения, компенсируется работой внешних сил.

Энергия, поглощаемая осциллятором в единицу времени от источника внешних сил, определяется выражением:

I() = m  ² b² = 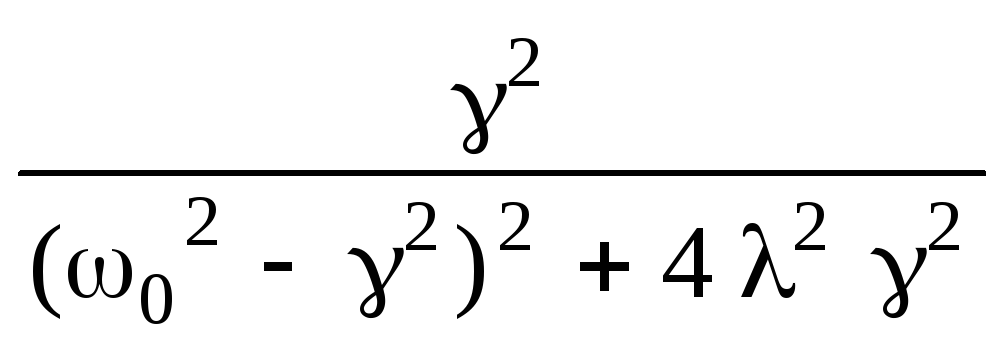. (18.11)

Максимальное поглощение энергии имеет место при = ₀.

Зависимость (18.11) вблизи острого максимума можно приблизительно описать формулой:

I() = , (18.12)

где =  – ₀. График функции I() называют резонансной кривой поглощения. Полуширина  резонансной кривой поглощения – такое значение  = , при которой интенсивность поглощения I() составляет половину ее максимального значения (I() = I_MAX / 2).

Из (18.12) следует, что

 = . (18.13)

Таким образом, полуширина кривой, равна коэффициенту затухания .

? Задания и контрольные вопросы

1. Объясните происхождение уравнения (18.3). Какой смысл имеют

входящие в него величины? Как решается это уравнение?

2. Расскажите о свободных колебаниях при наличии диссипативных

сил.

3*. Расскажите об апериодическом затухании.

4*. Объясните, как получаются формулы (18.8).

5. Нарисуйте графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы при различных коэффициентах сопротивления.

6. Расскажите об амплитудном резонансе.

7*. Выведите формулы (18.9) и (18.10).

8. Расскажите об энергетических превращениях в системе, совершающей вынужденные колебания.

9*. Расскажите о резонансной кривой поглощения и об измерении с ее помощью коэффициента затухания.

10*. Выведите формулу (18.13).