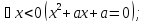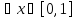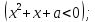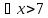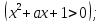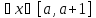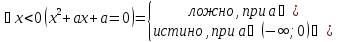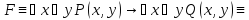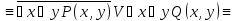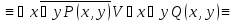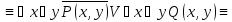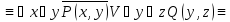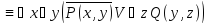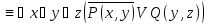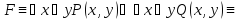- •Логика предикатов
- •§ 1. Основные понятия
- •§ 2. Классификация предикатов
- •Примеры:
- •§ 3. Множество истинности предиката
- •Примеры:
- •Утверждения:
- •Примеры:
- •§ 4. Равносильность предикатов
- •Пример 1
- •§ 5. Логические операции над предикатами Отрицание предиката
- •Примеры:
- •Пример 3
- •Предикат от n переменных и квантор общности
- •Квантор существования
- •Замечание
- •Предикат от n переменных и квантор существования
- •Замечание
- •Примечание
- •§ 7. Численные кванторы
- •Ограниченные кванторы
- •§ 8. Формулы логики предикатов
- •Определение формулы логики предикатов (по индукции)
- •§ 9. Классификация формул логики предикатов
- •Классификационные определения для формул логики предикатов
- •Значение формулы логики предикатов
- •§ 10. Тавтологии (равносильности) логики предикатов
- •Доказательство
- •§ 11. Равносильные преобразования формул
- •Пример неравносильных формул
- •§ 12. Общезначимость и выполнимость
- •Из определений следует:
- •Связь между общезначимостью и выполнимостью формул логики предикатов.
- •Проблема разрешения для общезначимости и выполнимости формул.
- •Решение проблемы для формул на конечных множествах.
- •Алгоритм распознавания общезначимости формул в частных случаях
- •Теорема 1
- •Следствие
- •Решение проблемы для -формул и-формул.
- •§ 13. Примеры и задачи
- •§ 14. Решение примеров
- •Решение
- •Решение
- •Решение
- •Решение примеров:
- •Литература
- •Содержание
§ 14. Решение примеров
На множестве M = {1, 2, 3, …, 20} заданы предикаты:
A (х): «х не делится на 5»;
B (х): «x - четное число»;
С(х): «х - число простое»;
D(х): «х кратно 3».
Найдите множества истинности предиката:

Решение:
Область истинности для предиката
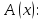
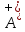 = M
= M {5,
10, 15, 20}
{5,
10, 15, 20}Область истинности для предиката
 : M
: M

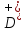 = M
= M {3,
6, 9, …, 18}
{3,
6, 9, …, 18}Область истинности для заданного предиката
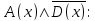
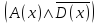 +
=
+
=
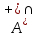 (
(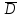 )+
=
M
)+
=
M {5,
10, 15, 20}
{5,
10, 15, 20}
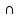 M
M {3,
6, 9, …, 18} =
{3,
6, 9, …, 18} == {1, 2, 4, 7, 8, 11, 13, 14, 16, 17, 19}
Найдите множества истинности предиката:
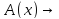
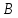 (x).
(x).
Решение:
Область истинности для предиката
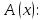
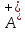 = M
= M {5,
10, 15, 20}
{5,
10, 15, 20}Область истинности для предиката
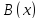 :
:
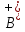 = {2, 4, 6, …, 20}
= {2, 4, 6, …, 20}Область истинности для заданного предиката
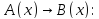
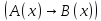 +
=
+
=
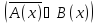 +
=(
+
=( )+
)+
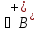 =(M
=(M =
=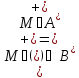
== {2, 4, 5, 6, 8, 10, 12, 14, 15, 16, 18, 20}
Установить, является следующее высказывание истинным или ложным, при условии, что область определения предикатов M совпадает с R:
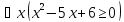
Решение
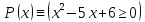
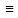 (x
– 3)(x
– 2)
(x
– 3)(x
– 2)
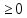 ,
,То есть область истинности предиката
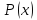 есть совокупность двух открытых
полусегментов:
есть совокупность двух открытых
полусегментов: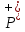 =
(-
=
(-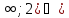
По определению
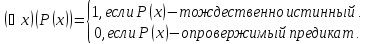
Предикат
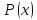 опровержимый для всехна
опровержимый для всехна
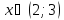 ,
следовательно, высказывание
,
следовательно, высказывание
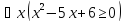 = 0.
= 0.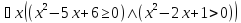
Решение
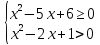 ,
,
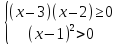 ,
т.е.
,
т.е.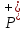 = (-
= (-
Т.к
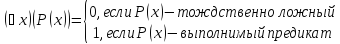 ,
то
,
то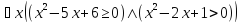 =
1, на
=
1, на
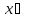 (-
(- – выполним
– выполним
Приведите примеры таких значений a, для которых данное высказывание: а) истинно; б) ложно. (M=R).
Решение
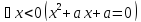
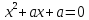
D =
 – 4a,
т.е P(x)
-выполнимый, при a
– 4a,
т.е P(x)
-выполнимый, при a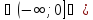 ,
при D
,
при D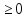
и P(x) –тождественно ложный, при a
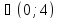 ,
приD
,
приD
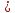 0, т.к тогда уравнение не имеет корней.
0, т.к тогда уравнение не имеет корней.По теореме Виета из уравнения
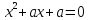 имеем
имеем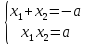
При D
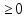 рассмотрим все случаи:
рассмотрим все случаи:
При a
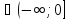 , т.е a
, т.е a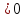 .
Если
.
Если
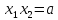 ,
значит
,
значит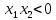 ,
следовательно
,
следовательно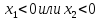 .
Т.е
.
Т.е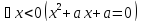
При a

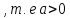 ,
если
,
если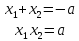 ,
значит
,
значит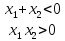 ,
следовательно
,
следовательно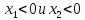 .
Т.е
.
Т.е
При a=0 имеем
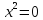 ,
т.еx
= 0.
,
т.еx
= 0.
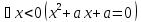 -
ложно
-
ложно
Даны утверждения
A(n): « число n делится на 3 »,
B(n): « число n делится на 2 »,
C(n): « число n делится на 4 »,
D(n): « число n делится на 6 »,
E(n): « число n делится на 12 ».
Укажите, какие из следующих утверждений истинны, какие ложны:
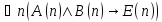 ;
;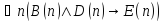 ;
;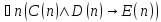 ;
;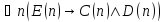 ;
; ;
;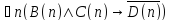 ;
; .
.
Решение примеров:
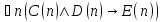
Область истинности для предиката
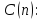
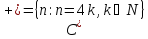
Область истинности для предиката
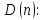
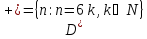
Область истинности для предиката
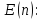
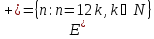
Область истинности для предиката
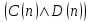 :
:
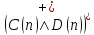 =
=
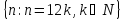
Области истинности для предикатов
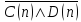 и
и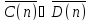 совпадают и равны:
совпадают и равны: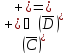
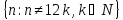 =
=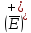
Тогда
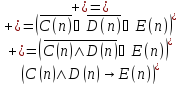

Таким образом, утверждение
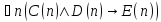 истинно
истинно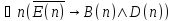
Область истинности для предиката
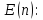

Область истинности для предиката
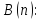
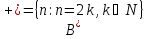
Область истинности для предиката
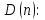
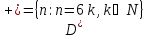
Область истинности для предиката
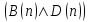 :
:
 =
=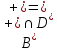
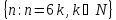
Тогда
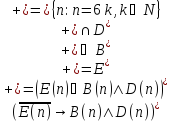
Таким образом, утверждение
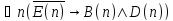 - ложно
- ложно
Пусть предикат
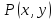 определен на множествеM
= N
определен на множествеM
= N
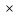 N
и означает «x<y».
N
и означает «x<y».Какие из следующих предикатов тождественно истинные и какие тождественно ложные:
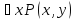 - выполнимый
предикат Q1(y)
- выполнимый
предикат Q1(y)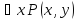 –тождественно-ложный
предикат Q2(y)
–тождественно-ложный
предикат Q2(y) –тождественно-истинный
предикат Q3(y)
–тождественно-истинный
предикат Q3(y)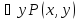 –тождественно-ложный
предикат Q4(y)
–тождественно-ложный
предикат Q4(y)
Для тех предикатов из 1), которые не являются ни тождественно истинными, ни тождестывенно ложными, указать область истинности и область ложности.
Q1 = {2,3,…,N}
Доказать следующую равносильность:
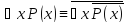
Доказательство:
Так как
 –
предикатная переменная, подставим
вместо нее конкретный предикат
–
предикатная переменная, подставим
вместо нее конкретный предикат
 и докажем, что:
и докажем, что:
По определению:
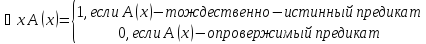
Пусть
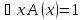 ,
тогда предикатA(x)
– тождественно-истинный, отсюда
,
тогда предикатA(x)
– тождественно-истинный, отсюда
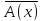 – тождественно-ложный предикат, отсюда
по определению связывания квантором
существования по переменнойx
предиката B(x)
получаем выказывание
– тождественно-ложный предикат, отсюда
по определению связывания квантором
существования по переменнойx
предиката B(x)
получаем выказывание
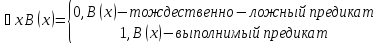
Отсюда следует, что высказывание
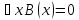 ,
значит отрицание этого высказывания
является истинным:
,
значит отрицание этого высказывания
является истинным:
Пусть
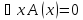 (*)
(*)
По определению:
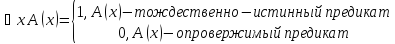
Из (*) следует, что
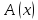 – опровержимый
предикат, тогда его отрицание
– опровержимый
предикат, тогда его отрицание
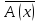 - выполнимый предикат.
- выполнимый предикат.Тогда высказывание
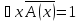 (**)
(**)А отрицание высказывания (**) равно нулю:
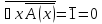
Доказать следующую равносильность:
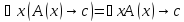
Доказательство:
По определению
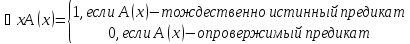 (*)
(*)1)Предположим, что
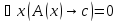
Тогда по определению (*),
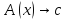 –опровержимый,
т.е.
–опровержимый,
т.е.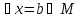 -предмет,
при котором
-предмет,
при котором
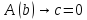 .
Получаем
.
Получаем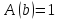 ,
,
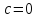
Т.к.
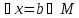 ,
что
,
что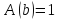 ,
то
,
то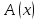 - доказуемый предикат, т.е.
- доказуемый предикат, т.е.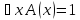
Тогда
 при
при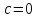
Следовательно
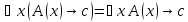
При
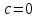
2) Предположим, что
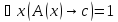
Тогда по определению (*),
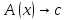 –тождественно
истинный, т.е.
–тождественно
истинный, т.е.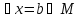 -предмет,
при котором
-предмет,
при котором
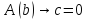 .
Получаем
.
ПолучаемЕсли
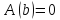 ,
то значениеc
не важно
,
то значениеc
не важно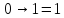
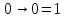
Если c=1, то значение
 не важно
не важно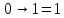
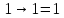
Т.к.
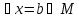 ,
что
,
что ,
то
,
то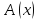 - доказуемый предикат, т.е.
- доказуемый предикат, т.е.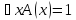
Тогда
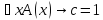 при
при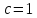
Следовательно
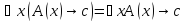
При
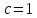
Доказать следующую равносильность:
1.
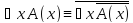
Законы де Моргана для кванторов
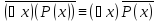
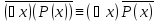
Доказательство.
Данная формула замкнута, т.е. не имеет свободных предметных переменных. Поэтому подставим в эту формулу вместо предикатной переменной
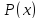 любой конкретный одноместный предикат
любой конкретный одноместный предикат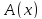 ,
определенный на некотором множестве
М=>получим высказывание
,
определенный на некотором множестве
М=>получим высказывание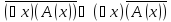 (*)
(*)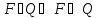 -тавтология
-тавтология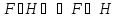
Для доказательства его истинности (*) нужно убедиться, что обе части эквивалентности одновременно истинны или одновременно ложны. В самом деле, высказывание
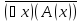 истинно тогда и только тогда, когда
высказывание
истинно тогда и только тогда, когда
высказывание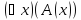 ложно, что возможно, на основании
определения, тогда и только тогда,
когда предикат
ложно, что возможно, на основании
определения, тогда и только тогда,
когда предикат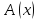 -опровержим:
-опровержим: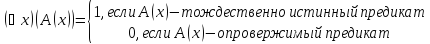
Далее, опровержимость предиката
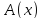 означает выполнимость предиката
означает выполнимость предиката ,
что равносильно истинности высказывания
,
что равносильно истинности высказывания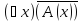 (по
определению)
(по
определению)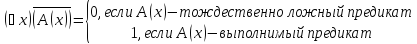
Итак, высказывание
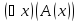 истинно тогда и только тогда, когда
высказывание
истинно тогда и только тогда, когда
высказывание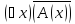 истинно. Следовательно, высказывание
(*) истинно, что и доказывает тождественную
истинность первой формулы.
истинно. Следовательно, высказывание
(*) истинно, что и доказывает тождественную
истинность первой формулы.
Найти отрицания следующих формул:
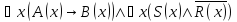
Решение:
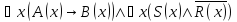
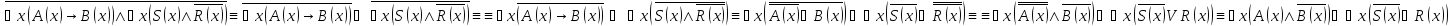
Даны два предиката Q(x, y) и R(y, z), определенные на множестве M
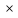 M,
где M = {a, b, c}.
Записать без использования кванторных
операций следующие формулы:
M,
где M = {a, b, c}.
Записать без использования кванторных
операций следующие формулы:
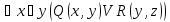 :
:Решение:
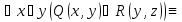
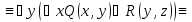
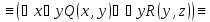
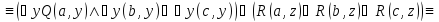
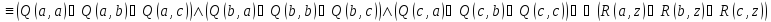
Привести к приведенной нормальной форме следующие формулы логики предикатов: