
2.Задача 2.6
а)Решить графическим методом следующие задачи линейного программирования.
f=-x1+2x2→ max (min),
x1-8x2≤10,
x1+x2≥1,
x1-5x2≥-5,
3x1+10x2≤30,
x1≥0, x2≥0.
Решение.
f=-x1+2x2→ max,
x1 -8x2 ≤ 10, (1)
x1 +x2 ≥ 1, (2)
x1 -5 x2 ≥-5, (3)
3x1+10x2≤30 (4)
x1 ≥ 0, x2 ≥ 0.
1.Строим область допустимых решений задачи. Нумеруем ограничения задачи.
2.Решаем уравнение х1 - 8х2 = 10,получаем две точки x1 = 0, x2 =-1,25 и x1 = =10, x2 =0.
В прямоугольной декартовой системе координат (рис. 2.1) по этим точкам строим прямую х1 - 8х2 = 10 (L1), соответствующую ограничению (1). Подставляем в неравенство координаты какой-либо точки, не лежащей на прямой. Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Стрелки на концах прямой L1 направлены в полуплоскость, которая является областью решений неравенства.
3. Решаем уравнение x1 +x2 =1,получаем две точки x1 = 0, x2 =1 и x1 = 1, x2 =0.
В прямоугольной декартовой системе координат (рис. 2.1) по этим точкам
строим прямую x1 +x2 =1 (L2), соответствующую ограничению (2). Подставляем в неравенство координаты какой-либо точки, не лежащей на прямой. Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (2). Стрелки на концах прямой L2 направлены в полуплоскость, которая является областью решений неравенства.
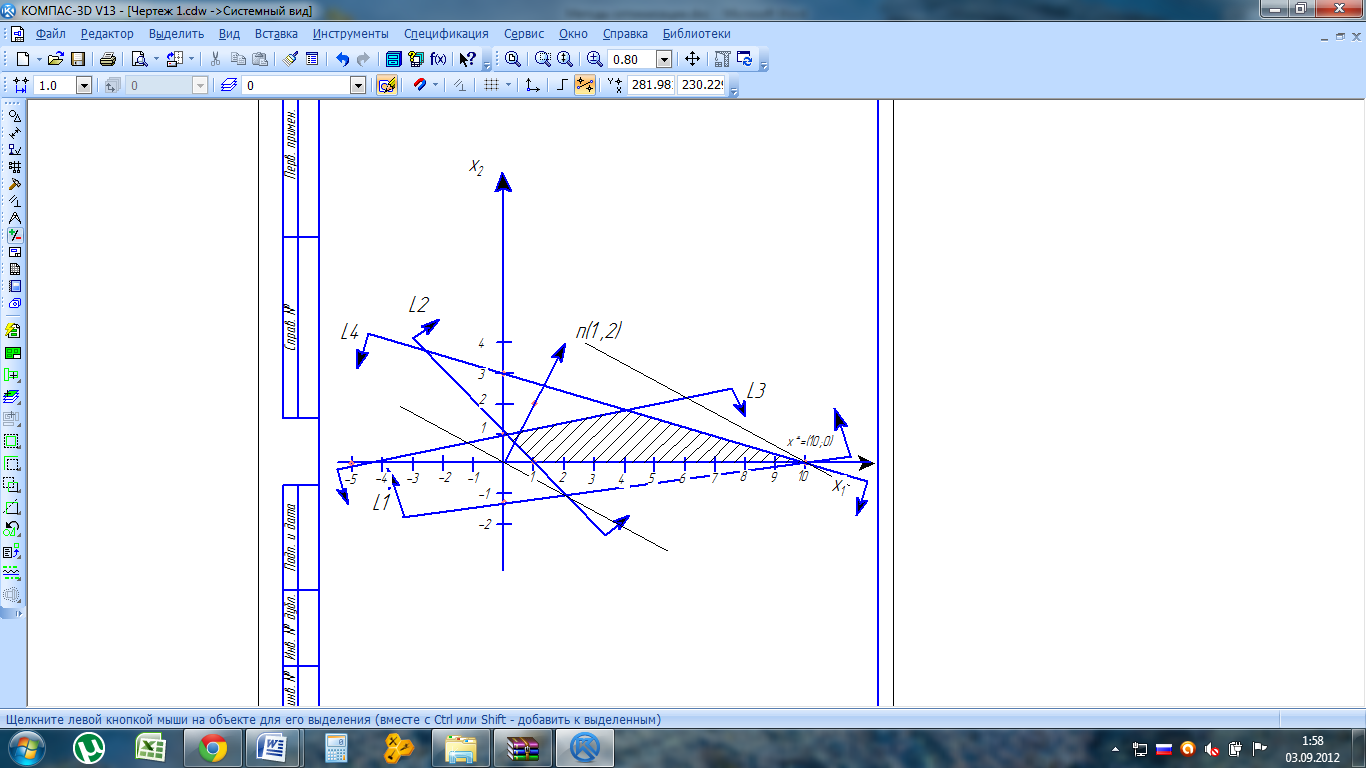
Рис.2.1
4. Решаем уравнение x1 -5 x2 =-5,получаем две точки x1 = 0, x2 =1 и x1 = -5, x2 =0.В прямоугольной декартовой системе координат (рис. 2.1) по этим точкам строим прямую x1 -5 x2 =-5 (L3), соответствующую ограничению (3). Подставляем в неравенство координаты какой-либо точки, не лежащей на прямой. Находим, какая из двух полуплоскостей, на которые эта прямая делит
всю координатную плоскость, является областью решений неравенства (3). Стрелки на концах прямой L3 направлены в полуплоскость, которая является областью решений неравенства.
5. Решаем уравнение 3x1+10x2=30,получаем две точки x1 = 0, x2 =1 и x1 = -5, x2 =0.В прямоугольной декартовой системе координат (рис. 2.1) по этим точкам строим прямую 3x1+10x2=30 (L4), соответствующую ограничению (4). Подставляем в неравенство координаты какой-либо точки, не лежащей на прямой. Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (4). Стрелки на концах прямой L4 направлены в полуплоскость, которая является областью решений неравенства.
6.Находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности; полученную область допустимых решений отметим на рис. 2.1 штриховкой.
7.Строим нормаль линий уровня ñ = (1, 2) и линию уровня, например x1+2x2=0. Так как решается задача на отыскание максимума целевой функции,
то линию уровня перемещаем в направлении нормали до опорной прямой. Эта прямая проходит через точку X* пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (4). Определяем, координаты точки X*=L1∩L4.
Решаем систему x1 -8x2 = 10 , x1 =8x2 + 10,
3x1+10x2=30 ; 3(8x2 + 10)+10x2=30
34x2 =30-30; x2 =0 ; x1=10
получаем X* = (10, 0)
Вычисляем Z(X*) = x1+2x2=10 + 2 • 0 = 10.
Ответ: max Z(X) = 10 при X* = (10, 0).
б)Решить графическим методом следующие задачи линейного программирования.
f=-x1+2x2→min,
x1-8x2≤10,
x1+x2≥1,
x1-5x2≥-5,
3x1+10x2≤30,
x1≥0, x2≥0.
Решение: f=-x1+2x2→ min
x1 -8x2 ≤ 10, (1)
x1 +x2 ≥ 1, (2)
x1 -5 x2 ≥-5, (3)
3x1+10x2≤30 (4)
x1 ≥ 0, x2 ≥ 0.
В задаче на отыскание минимума функции выполняем пункты с 1по 5 предыдущей задачи на отыскание максимума функции. Строим область допустимых решений, нормаль линий уровня ñ = (1, 2) и одну из линий уровня, имеющую общие точки с этой областью (рис. 2.). Перемещаем линию уровня в направлении, противоположном направлению нормали ñ, так как решается задача на отыскание минимума функции.
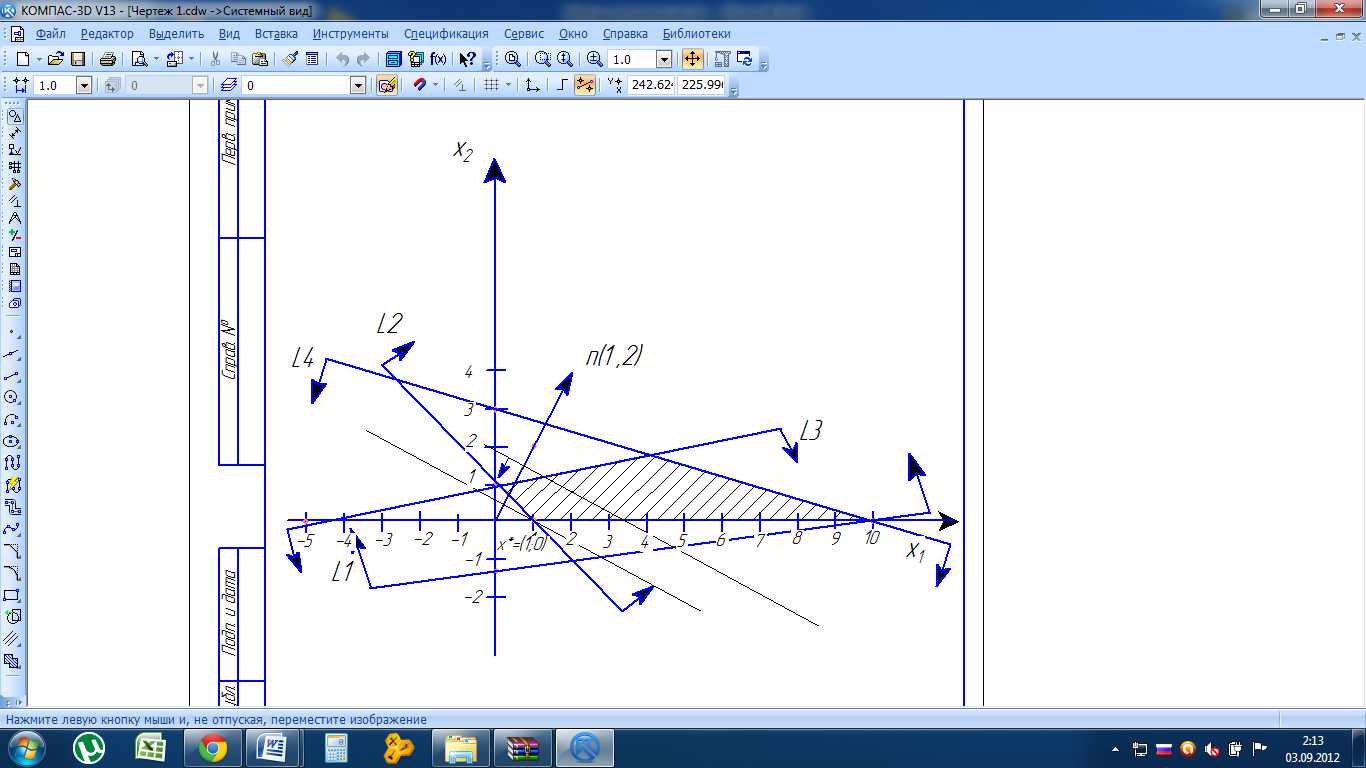
Рис.2.2
Опорная прямая проходит через точку пересечения прямой L2 и оси абсцисс х1. Эту точку Х*=L2∩ х1, находим, решая систему уравнений:
x1 +x2 =1 x1 =1 X *= (1, 0)
x2=0 ; x2 =0 Вычисляем Z(X*) = x1+2x2=1 + 2 • 0 = 1.
Ответ: min Z(X) = 1.
