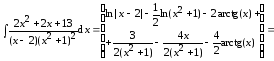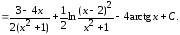- •1. Первообразная. Неопределённый интеграл
- •Вопросы для самопроверки.
- •2. Свойства неопределённого интеграла.
- •Вопросы для самопроверки.
- •3. Внесение функции под знак дифференциала
- •Вопросы для самопроверки.
- •4. Метод замены аргумента
- •Вопросы для самопроверки
- •5. Интегрирование по частям. Рекурре;´нтные4формулы
- •Вопросы для самопроверки.
- •6. Интегрирование рациональных5дробей
- •Вопросы для самопроверки.
- •7. Интегрирование иррациональных7функций
- •Вопросы для самопроверки.
- •8. Интегрирование тригонометрических выражений
- •Вопросы для самопроверки.
- •9. Нахождение неопределенных интегралов с помощью справочника
- •Ответы к примерам из вопросов для самопроверки
5. Интегрирование по частям. Рекурре;´нтные4формулы
Рассмотрим
дифференциал произведения функций
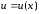 и
и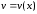
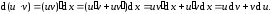
Итак,
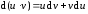 .
(5.1)
.
(5.1)
Проинтегрируем обе части равенства (5.1)
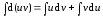 .
.
Отсюда
 (5.2)
(5.2)
Эта формула называется формулой интегрирования по частям.
Пример. 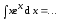
Обозначим 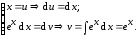
Тогда
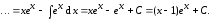
Теперь
рассмотрим полезный для будущего пример
(для
 )
)
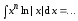
Обозначим 
Тогда
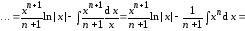
 (5.3)
(5.3)
В
частности, при
 получаем следующее важное дополнение
к таблице основных интегралов
получаем следующее важное дополнение
к таблице основных интегралов
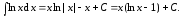 (5.4)
(5.4)
Формулу
интегрирования по частям целесообразно
использовать в случае, если вычисление
интеграла
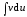 легче осуществить, чем вычисление
интеграла
легче осуществить, чем вычисление
интеграла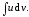
Теперь последовательно рассмотрим два интеграла
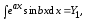
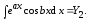
1.
Пусть 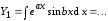

Тогда
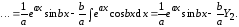
2.
Пусть 
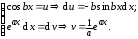
Тогда

Получаем систему
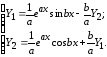
Отсюда
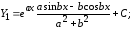 (5.5)
(5.5)
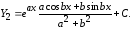 (5.6)
(5.6)
Продемонстрируем метод последовательного понижения степени у подынтегральной функции на следующем примере
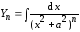 .
.
Здесь
 − целое положительное число.
− целое положительное число.
При
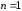 получаем, как частный случай, формулу
(4.2).
получаем, как частный случай, формулу
(4.2).
Пусть
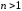 .
Представим единицу в числителе
подынтегральной функции в виде
.
Представим единицу в числителе
подынтегральной функции в виде
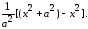
Тогда получим

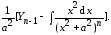
Для вычисления второго интеграла применяем метод интегрирования по частям
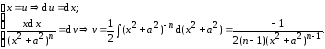
Получим
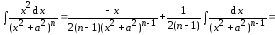
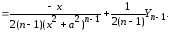
Следовательно,
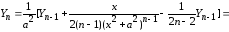
 (5.7)
(5.7)
Таким образом,
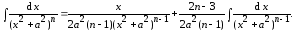 (5.8)
(5.8)
За счёт применения интегрирования по частям удалось получить формулу (5.8) и уменьшить показатель степени знаменателя подынтегральной функции на единицу. Продолжая идти тем же путём, можно дойти до интеграла (4.2). Формулы типа (5.8) и называются рекуррентными.
Вопросы для самопроверки.
1. Выведите формулу интегрирования по частям для неопределён-ного интеграла.
2. Укажите примеры интегралов, вычисление которых целесообраз-но производить при помощи метода интегрирования по частям.
3. Найдите
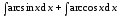 и объясните получающийся результат.
и объясните получающийся результат.
4. Попробуйте
применить метод интегрирования по
частям к интегралу
 ,
полагая
,
полагая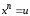 ,
,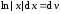 ,
и сделайте сравнение с ходом решения
того же примера при выведении формулы
(5.3).
,
и сделайте сравнение с ходом решения
того же примера при выведении формулы
(5.3).
5. Каково предназначение рекуррентных формул?
Используя формулу (5.8), найдите
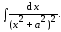
Результат проверьте по справочнику.
6. Интегрирование рациональных5дробей
Методом деления числителя на знаменатель любую неправильную дробь можно представить в виде суммы многочлена и правильной дроби6, поэтому интегрирование неправильных дробей сводится к интегрированию многочлена и правильной дроби.
Пример
1. 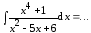
Здесь интегрируемая дробь – неправильная, поэтому надо выделить целую часть и остаток деления «столбиком» (или по методу Горнера)
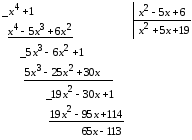
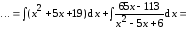

Вычисление последнего интеграла должно быть получено в ответе на 6-й вопрос для самопроверки в конце настоящего параграфа.
Пример
2. Рассмотрим интеграл вида
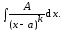
При
 имеем
имеем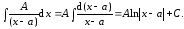
При


Теперь
рассмотрим интеграл вида 
Преобразуем
квадратный трёхчлен
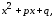 стоящий в знаменателе подынтегральной
функции, к сумме квадратов
стоящий в знаменателе подынтегральной
функции, к сумме квадратов
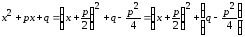
Если
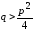 ,
обозначим
,
обозначим 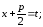
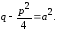
Тогда 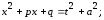

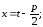
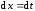 .
.
Пусть,
для начала,
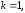 тогда
тогда
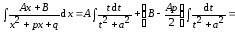

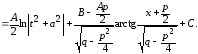
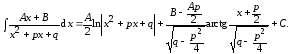 (6.1)
(6.1)
При
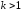 и
и
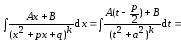
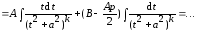
Обозначим

Тогда
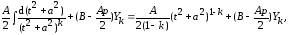
где
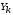 далее преобразуется по формуле (5.8).
далее преобразуется по формуле (5.8).
В итоге получаем
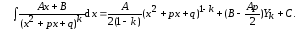 (6.2)
(6.2)
Теперь рассмотрим несколько конкретных примеров, в каждом из которых подынтегральная функция является правильной рациональной дробью.
Пример
3. Случай, когда знаменатель подынтегральной
функции имеет только действительные
различные корни 
Подынтегральная функция является правильной рациональной дробью. Разложим её на простейшие
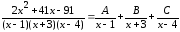 ,
,
где
 – неизвестные коэффициенты, подлежащие
определению.
– неизвестные коэффициенты, подлежащие
определению.
Освобождаясь от знаменателей в обеих частях равенства, получаем
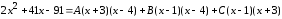 ,
,
или

Приравнивая коэффициенты при одинаковых степенях x слева и справа от знака равенства, получим систему трёх уравнений с тремя неизвестными
при 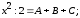
при 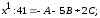
при 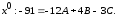
Решая эту систему, найдем А = 4; В = – 7; С = 5.
Итак,
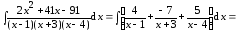
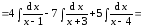
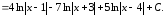
Пример 4. Случай, когда знаменатель подынтегральной функции имеет только действительные корни, причём некоторые из них − кратные
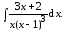
Разложим подынтегральную функцию на простейшие дроби
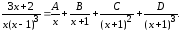
Приводя
правую часть к общему знаменателю и
приравнивая коэффициенты при одинаковых
степенях
 в левой и правой частях равенства,
получаем систему алгебраических
уравнений относительно неизвестных
коэффициентов разложения на простейшие
дроби.
в левой и правой частях равенства,
получаем систему алгебраических
уравнений относительно неизвестных
коэффициентов разложения на простейшие
дроби.
Решая полученную систему уравнений, находим, что
А = 2; В = – 2; С = – 2; D = 1.
Следовательно,

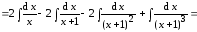
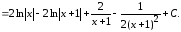
Пример
5. Случай, когда знаменатель имеет
различные, в том числе - комплексные,
корни 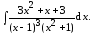
Разложим подынтегральную функцию на простейшие дроби

Как
и в предыдущих примерах, приравниваем
коэффициенты при одинаковых степенях
 .
В результате решения образовавшейся
системы уравнений получаем
.
В результате решения образовавшейся
системы уравнений получаем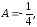
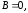
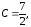
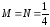 .
.
Следовательно,
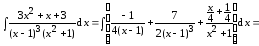
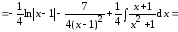
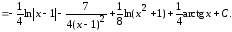
Пример
6. Случай, когда знаменатель подынтегральной
функции имеет кратные комплексные
корни 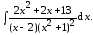
Разлагаем подынтегральную функцию на простейшие дроби

Приравнивая
коэффициенты при одинаковых степенях
 ,
получаем систему уравнений, из которой
находим
,
получаем систему уравнений, из которой
находим
А = 1; В = – 1; С = – 2; D = – 3, Е = – 4.
Тогда