Вопросы для самопроверки.

1. Перечислите основные свойства неопределённого интеграла. Как они доказываются?

2. Чему равны следующие интегралы:

а) 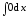; б).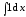

3. Найдите .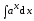

4. Напишите таблицу простейших интегралов на память.

5. Найдите интеграл .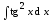

Указание: используйте известное тригонометрическое соотношение

.

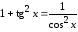3. Внесение функции под знак дифференциала

Всякая формула интегрирования справедлива независимо от того, является ли переменная интегрирования независимой переменной или любой непрерывно дифференцируемой функцией независимой переменной, то есть из справедливости равенства

(3.1)

следует справедливость равенства

, (3.2)

где 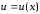– любая непрерывно дифференцируемая функция аргумента x.

Применение основного правила, следующего из определения дифференциала функции,

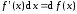(3.3)

демонстрируется на следующих примерах.

Пример 1. .

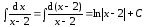Пример 2. .

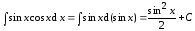Пример 3. .

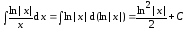Пример 4. .

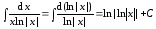Иллюстрация рассмотренного приёма вынесена в отдельный параграф, т. к. этот способ очень часто оказывается эффективным и должен быть хорошо отработан на практике.

Вопросы для самопроверки.

1. Вычислите интеграл .

2. Найдите .

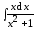3. Применяя формулу (3.3), найдите .

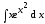4. Найдите .

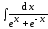5. Найдите .

.

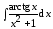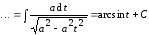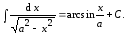
6. Найдите .

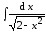4. Метод замены аргумента

Метод введения нового аргумента (метод подстановки) основан на следующей теореме.

Теорема. Если 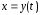и существует производная, то

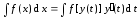. (4.1)

Используя эту теорему, расширим таблицу простейших интегралов, приведённых в § 2.

Пример 1.

Обозначим , тогда.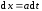

.

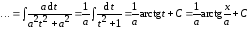Таким образом,

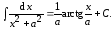^(4.2)

Полученная формула является обобщением формулы (2.16). Последняя получается из (4.2) при .

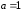Пример 2.

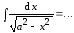
Пусть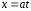, тогда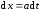. (4.3)

Полученная формула является обобщением формулы (2.15). Целесообразно сравнить ход решения примера (4.3) с решением примера 6 из вопросов для самопроверки предыдущего параграфа.

Пример 3.

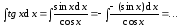
Положим 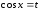, тогда,

.

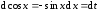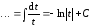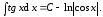(4.4)

Если ,

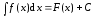то Теперь следует обратиться к первому из вопросов для самопроверки в конце данного параграфа, связанному с формулой (4.6).

Указание: в процессе вывода формул (4.4) и (4.6) необходимо использовать общее правило: если числитель подынтегральной функции есть производная её знаменателя, то интеграл равен натуральному логарифму модуля знаменателя, т.е.

; .

.

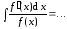
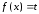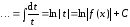Пример 4.

.

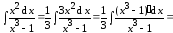
Пример 5.

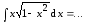
Делаем замену переменной по соотношению ,

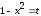тогд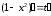а ; отсюда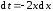и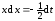

.

Пример 6.

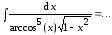
Обозначим 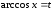, тогда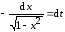

.

Применяя метод введения нового аргумента, можно добавить к изученным свойствам неопределённого интеграла ещё одно полезное соотношение (свойство):

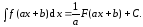(4.5)

Доказательство.

Очевидно,

; ;.

.

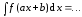
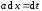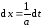Пример 7. .

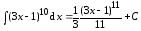Пример 8. .

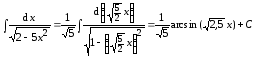Вопросы для самопроверки

1. Покажите, что

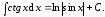(4.6)

2. Выведите формулу замены переменной в неопределённом интеграле.

3. Найдите 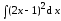двумя способами:

а) раскройте скобки возведением разности в квадрат, проинтегрируйте получающуюся сумму;

б) непосредственно, как интеграл от степенной функции со сложным аргументом, используя формулу (4.5).

Покажите, что полученные результаты не противоречат друг другу.

4. Найдите .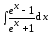

5. Укажите целесообразные подстановки в следующие примеры и найдите первообразные:

а) ;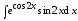

б) ;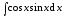

в) ;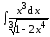

г) 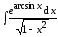.