
- •РАБОЧАЯ ТЕТРАДЬ ПО ТЕМАМ 6.1, 6.2
- •Тема 6.1. Интегрирование функций нескольких переменных
- •Двойной интеграл
- •Задача 1.1
- •Задача 1.2
- •Справочный материал
- •Решение задачи 1.1
- •Решение задачи 1.2
- •Задача 2.1
- •Задача 2.2
- •Справочный материал
- •Механический смысл двойного интеграла
- •Геометрический смысл двойного интеграла
- •Решение задачи 2.1
- •Решение задачи 2.2
- •Тройной интеграл
- •Задача 3.1
- •Задача 3.2
- •Задача 3.3
- •Справочный материал
- •Решение задачи 3.1
- •Решение задачи 3.2
- •Тройной интеграл в сферических координатах
- •Решение задачи 3.3
- •Задача 4.1
- •Задача 4.2
- •Задача 4.3
- •Справочный материал
- •Решение задачи 4.1
- •Решение задачи 4.2
- •Решение задачи 4.3.
- •Задача 5.1
- •Задача 5.2
- •Задача 5.3
- •Справочный материал
- •Решение задачи 5.1
- •Решение задачи 5.2
- •Решение задачи 5.3
- •Задача 6.1
- •Задача 6.2
- •Задача 6.3
- •Справочный материал
- •Решение задачи 6.1
- •Решение задачи 6.2
- •Решение задачи 6.3
- •Тема 6.2. Теория поля
- •Скалярное поле
- •Задача 7.1
- •Задача 7.2
- •Задача 7.3
- •Справочный материал
- •Решение задачи 7.1
- •Решение задачи 7.2
- •Решение задачи 7.3
- •Векторное поле
- •Задача 8.1
- •Задача 8.2
- •Справочный материал
- •Решение задачи 8.1
- •Решение задачи 8.2
- •Задача 9.1
- •Задача 9.2
- •Справочный материал
- •Решение задачи 9.1
- •Решение задачи 9.2
- •Задача 10
- •Справочный материал
- •Теорема Стокса
- •Решение задачи 10
- •Задача 11
- •Справочный материал
- •Решение задачи 11
- •Задания к типовым расчетам
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •ПРИЛОЖЕНИЕ
- •Полярная система координат
- •Эллиптические координаты
- •Сферическая система координат
- •Обобщенно эллиптические координаты
- •Механические приложения интегралов функций нескольких переменных
- •Механические приложения двойных интегралов
- •Статические моменты
- •Координаты центра тяжести
- •Моменты инерции
- •Механические приложения тройного интеграла
- •Статические моменты
- •Координаты центра тяжести
- •Моменты инерции
- •Механические приложения криволинейного интеграла первого рода
- •Статические моменты дуги
- •Координаты центра тяжести дуги
- •Моменты инерции дуги
- •Механические приложения поверхностного интеграла первого рода
- •Статические моменты участка поверхности
- •Моменты инерции участка поверхности

|
|
|
|
|
1−x2 |
|
|
|
|
|
|
− x2 |
= |
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||
V = ∫∫∫1dV = ∫∫dx dy |
∫dz = ∫∫dx dy z |
|
0 |
|
|
||||||||||||||
|
Ω |
D |
|
0 |
D |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
1−x |
|
1 |
(1 − x2 )(1 − x)dx = |
||||||||||
= ∫∫(1 − x2 )dx dy = ∫ |
(1 − x2 )dx ∫dy = ∫ |
||||||||||||||||||
D |
|
|
0 |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
(1 − x |
2 |
|
3 |
)dx = |
|
x3 |
|
|
x2 |
|
|
x4 |
|
1 |
|
|||
|
|
|
|
|
|
|
|||||||||||||
= ∫ |
|
− x + x |
|
x − |
|
− |
|
|
+ |
|
|
|
|
|
0 |
= |
|||
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
4 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
=1 − 13 − 12 + 14 = 125 .
Решение задачи 3.2
Объем тела вычисляется по формуле
V = ∫∫∫1 dV .
Ω
Область интегрирования Ω показана на рисунке 10. Ее удобно проектировать в плоскость yOz . Чтобы найти проекцию области Ω,
определим |
линию |
пересечения |
заданных |
поверхностей: |
|||
|
|
2 |
+ z |
2 |
|
|
|
x = y |
|
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
x |
=1 |
|
|
|
|
|
|
|
|
|
|
|||
z 
x = y2 + z2
x =1 |
y |
1
x
Рис. 10.
16
|
2 |
+ z |
2 |
=1 |
|
y |
|
|
, из которого ясно, что |
||
Преобразуем систему к виду |
|
|
|
|
|
|
|
x =1 |
|
|
|
|
|
|
|
||
линией пересечения является окружность с радиусом 1, лежащая в плоскости x =1.
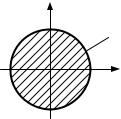
Следовательно, область интегрирования проектируется в координатную плоскость yOz на круг с радиусом, равным 1 (рис. 11).
|
|
y |
|
|
|
|
ρ =1 |
|
|
|
D |
|
|
|
|
|
|
x |
|
|
|
Рис. 11. |
|
|
Тройной интеграл по области Ω сведется к двойному интегралу |
||||
по области |
D (рис. 11). Пределы интеграции для переменной |
x |
||
определяются из неравенства: |
y2 + z 2 ≤ x ≤1 . |
|
||
|
|
|
1 |
|
|
V = ∫∫∫1 dV = ∫∫1dydz |
∫dx = |
|
|
|
Ω |
D |
y2 +z2 |
|
|
|
2 1 |
|
|
∫∫(1− y2 − z2 )dydz . |
||||||||
= ∫∫ dydz x |
y |
|
2 = |
||||||||||
D |
|
+ z |
|
|
D |
|
|
|
|
|
|||
Область интегрирования |
|
D |
|
- |
круг. |
Поэтому перейдем к |
|||||||
полярным координатам. |
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ρcos ϕ |
, |
y |
2 |
+ z |
2 |
= ρ |
2 |
, |
0 ≤ ϕ ≤ 2π |
. |
|||
|
|
|
|
|
|
0 ≤ ρ ≤1 |
|||||||
z = ρsin |
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
V = ∫∫(1 −ρ2 )ρdρdϕ = 2∫πdϕ1∫(ρ −ρ3 )dρ = |
|||||||||||||
D |
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
17
