
- •44.1. Частные производные первого порядка и их геометрическое истолкование
- •44.2. Частные производные высших порядков
- •44.3. Дифференцируемость и полный дифференциал функции
- •44.4. Применение полного дифференциала к приближенным вычислениям
- •44.5. Дифференциалы высших порядков
- •44.6. Производная сложной функции. Полная производная
- •44.7. Инвариантность формы полного дифференциала
- •44.8. Дифференцирование неявной функции
- •Необходимое и достаточное условие интегрируемости.
- •Формула Ньютона – Лейбница
- •40.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)
- •40.2. Интеграл от разрывной функции (несобственный интеграл II рода)
- •42.1. Формула прямоугольников
- •42.2. Формула трапеций
- •42.3. Формула парабол (Симпсона)
40.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)
Пусть
функция ƒ(х) непрерывна на промежутке
[а;+∞). Если существует конечный предел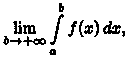 то
его называют несобственным
интегралом первого родаи
обозначают
то
его называют несобственным
интегралом первого родаи
обозначают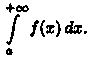
Таким образом, по определению

В
этом случае говорят, что несобственный
интеграл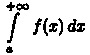 сходится.
сходится.
Если
же указанный предел не существует или
он бесконечен,то говорят, что
интеграл 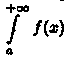 dx расходится.
dx расходится.
Аналогичноопределяется
несобственный интеграл на промежутке
(-∞; b]: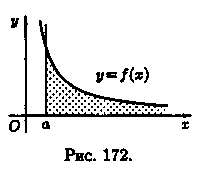
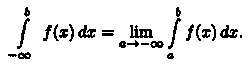
Несобственный интеграл с двумя бесконечны ми пределами определяется формулой
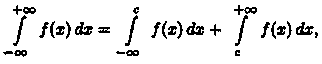 где
с — произвольное число.
где
с — произвольное число.
В
этом случае интеграл слева сходится
лишь тогда, когда сходятся оба интеграла
справа. Отметим, что если непрерывная
функция ƒ (х) ≥ 0 на промежутке [а; +∞) и
интеграл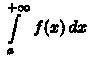 сходится,
то он выражает площадь бесконечно
длинной криволинейной трапеции (см.
рис. 172).
сходится,
то он выражает площадь бесконечно
длинной криволинейной трапеции (см.
рис. 172).
Пример 40.1. Вычислить несобственные интегралы или установить их расходимость:
1) 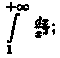 2)
2)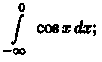 3)
3)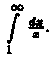
Решение:
1)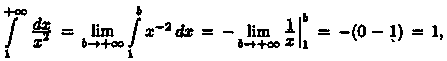 интеграл
сходится;
интеграл
сходится;
2)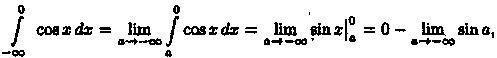 интеграл
расходится, так как при а →-∞ предел
интеграл
расходится, так как при а →-∞ предел![]() не
существует.
не
существует.
3)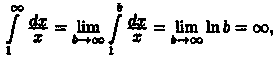 интеграл
расходится.
интеграл
расходится.
В некоторых задачах нет необходимости вычислять интеграл; достаточно лишь знать, сходится ли он или нет.
Приведем без доказательства некоторые признаки сходимости.
Теорема 40.1 (признак сравнения). Если на промежутке [а; +∞) непрерывные функции ƒ(х) и φ(х) удовлетворяют условию 0 ≤ ƒ(х) ≤φ(х), то из сходимости
интеграла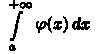 следует
сходимость интеграла
следует
сходимость интеграла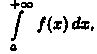 а
из расходимо-
а
из расходимо-
сти
интеграла 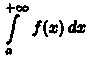 следует
расходимость интеграла
следует
расходимость интеграла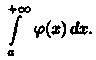
Пример
40.2. Сходится ли интеграл
Решение:
При х ≥ 1 имеем![]() Но
интеграл
Но
интеграл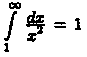 сходится.
Следовательно, интеграл
сходится.
Следовательно, интеграл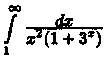 также
сходится (и его значение меньше 1).
также
сходится (и его значение меньше 1).
Теорема
40.2. Если существует предел![]() и φ(х)
> 0), то интегралы
и φ(х)
> 0), то интегралы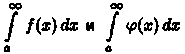 одновременно
оба сходятся или оба расходятся (т. е.
ведут себя одинаково в смысле сходимости).
одновременно
оба сходятся или оба расходятся (т. е.
ведут себя одинаково в смысле сходимости).
Пример
40.3. Исследовать сходимость интеграла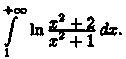
Решение:
Интеграл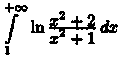 сходится,
так как интеграл
сходится,
так как интеграл 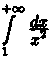 сходится
и
сходится
и
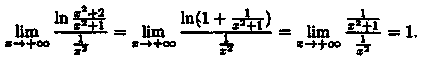
40.2. Интеграл от разрывной функции (несобственный интеграл II рода)
Пусть
функция ƒ(х) непрерывна на промежутке
[а; b) и имеет бесконечный разрыв при х =
b. Если существует конечный предел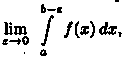 то
его называют несобственным интегралом
второго рода и обозначают
то
его называют несобственным интегралом
второго рода и обозначают 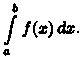
Таким образом,поопределению,
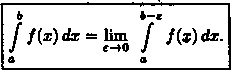
Если
предел в правой части существует, то
несобственный интеграл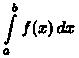 сходится.
Если же указанный предел не существует
или бесконечен,то говорят, что
интеграл
сходится.
Если же указанный предел не существует
или бесконечен,то говорят, что
интеграл 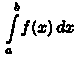 расходится.
расходится.
Аналогично,если
функция ƒ (х) терпит бесконечный разрыв
в точке х = а, то полагают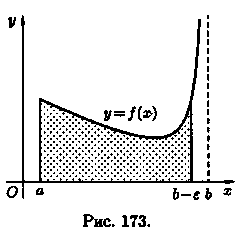
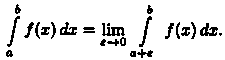
Если функция ƒ(х) терпит разрыв во внутренней точке с отрезка [а; b], то несобственный интеграл второго рода определяется формулой

В
этом случае интеграл слева называют
сходящимся, если оба несобственныхинтеграла,
стоящих справа, сходятся. В случае, когда
ƒ(х) > 0, несобственный интеграл второго
рода 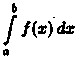 (разрыв
в точке х = b) можно истолковать геометрически
как площадь бесконечно высокой
криволинейной трапеции (см. рис. 173).
(разрыв
в точке х = b) можно истолковать геометрически
как площадь бесконечно высокой
криволинейной трапеции (см. рис. 173).
Пример
40.4. Вычислить![]()
Решение:
При х = 0 функция ![]() терпит
бесконечный разрыв;
терпит
бесконечный разрыв;
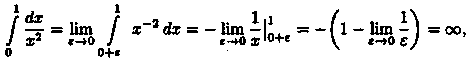
интеграл расходится.
Сформулируем признаки сходимости для несобственных интегралов второго рода.
Теорема 40.3. Пусть на промежутке [а; b) функции ƒ(х) и φ(х) непрерывны, при х = b терпят бесконечный разрыв и удовлетворяют условию 0 ≤ ƒ(х) ≤ φ(x).
Из
сходимости интеграла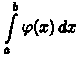 вытекает
сходимость интеграла
вытекает
сходимость интеграла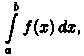 а
из расходимости интеграла
а
из расходимости интеграла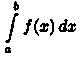 вытекает
расходимость интеграла
вытекает
расходимость интеграла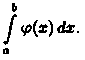
Теорема
40.4. Пусть функции ƒ(х) и φ(х) непрерывны
на промежутке [а; b) и в точке х = b терпят
разрыв. Если существует предел![]() то
интегралы
то
интегралы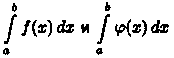 одновременно
сходятся или одновременно расходятся.
одновременно
сходятся или одновременно расходятся.
Пример
40.5. Сходится ли интеграл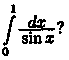
Решение:
Функция![]() имеет
на [0; 1] единственный разрыв в точке х =
0. Рассмотрим функцию
имеет
на [0; 1] единственный разрыв в точке х =
0. Рассмотрим функцию![]() ,
Интеграл
,
Интеграл
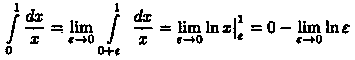
расходится. И так как
![]()
то
интеграл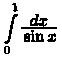 также
расходится.
также
расходится.
Пусть
требуется найти определенный интегралот
непрерывной функции ƒ(х). Если можно
найти первообразную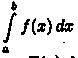 F(x)
функции ƒ(х), то интеграл вычисляется
по формуле Ньютона-Лейбница:
F(x)
функции ƒ(х), то интеграл вычисляется
по формуле Ньютона-Лейбница:
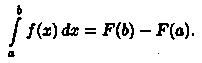
Но отыскание первообразной функции иногда весьма сложно; кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этих и других случаях (например, функция у = ƒ(х) задана графически или табличнo) прибегают к приближенным формулам, с помощью которых определенный интеграл находится с любой степенью точности.
Рассмотрим три наиболее употребительные формулы приближенного вычисления определенного интеграла — формулу прямоугольников, формулу трапеций, формулу парабол (Симпсона), основанные на геометрическом смысле определенного интеграла.
