44.7. Инвариантность формы полного дифференциала

Используя правило дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности: полный дифференциал функции z=ƒ(х;у) сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.

Пусть z=ƒ(х;у), где х и у — независимые переменные. Тогда полный дифференциал (1-го порядка) функции имеет вид

 (формула (44.5)).

Рассмотрим сложную функцию z=ƒ(х;у), где х = x(u;v), у = y(u;v), т. е. функцию z = f(x(u;v);y(u;v)) = F(u;v;), где u и v — независимые переменные. Тогда имеем:

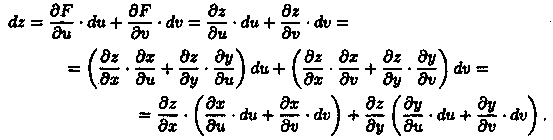
Выражения в скобках представляют собой полные дифференциалы dx и dy функций х = х(u;v) и y = y(u;v). Следовательно, и в этом случае,

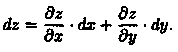
44.8. Дифференцирование неявной функции

Функция z = ƒ (х; у) называется неявной, если она задается уравнением

неразрешенным относительно z. Найдем частные производные неявной функции z, заданной уравнением (44.11). Для этого, подставив в уравнение вместо z функцию ƒ (х; у), получим тождество F(x;у;ƒ (х; у)) = 0. Частные производные по х и по у функции, тождественно равной нулю, также равны нулю:

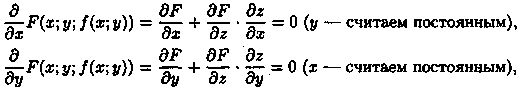
откуда

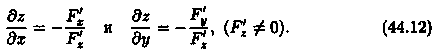
Замечания.

а) Уравнение вида (44.11) не всегда определяет одну переменную как неявную функцию двух других. Так, уравнение х²+у²+z²-4=0 определяет функцииопределенные в круге х²+у²≤4,определенную в полукруге х2+у2 ≤ 4 при у≥ 0 и т. д., а уравнение cos(x + 2у +3z)- 4 = 0 не определяет никакой функции.

Имеет место теорема существования неявной функции двух переменных: если функция F(x; у; z) и ее производные F'x(x; у; z), F'y(x; у; z), F'z(x;y;z) определены и непрерывны в некоторой окрестности точки M0(x₀;y₀;z₀), причем F(x₀;y₀;z₀)=0, а F'z(x₀;y₀;z₀)≠0, то существует окрестность точки М₀, в которой уравнение (44.11) определяет единственную функцию z=ƒ(х;у), непрерывную и дифференцируемую в окрестности точки (х₀;у₀) и такую, что ƒ(х₀;у₀)=z₀.

б) Неявная функция у=ƒ(х) одной переменной задается уравнением F(x;у)=0. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле

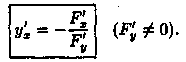
Пример 44.6. Найти частные производные функции z, заданной уравнением e^z+z-х²у+1=0.

Решение: Здесь F(x;y;z)=e^z+z-х²у+1, F'_x=-2ху, F'_y = -х2, F'_z=e^z+1. По формулам (44.12) имеем:

Пример 44.7. Найти если неявная функция у=ƒ(х) задана уравнением у³+2у=2х.

Решение: Здесь F(x;у) = у³+2у-2х, F'_x=-2, F'_y = 3у²+2. Следовательно,

Необходимое и достаточное условие интегрируемости.

Теорема. Для того, чтобы ограниченная на некотором отрезке функция была интегрируема на нем необходимо и достаточно, чтобы lim∣τ∣→0(Sτ−sτ)=0  (2.1).  Это условие означает, для любого ε>0 существует δ(ε)>0, что для любого разбиения τ мелкости меньше, чем δ выполняется неравенство: ∣Sτ−sτ∣<ε  (2.2). Т.к. sτ≤Sτ , то из (2.2) следует Sτ−sτ<ε . Доказательство.  Необходимость. Пусть некоторая ограниченная на [a,b] функция f интегрируема на нем и I=∫baf(x)dxт.е.lim∣τ∣→0στ=I. Поэтому для любого ε>0 существует δ(ε)>0, что для  любого разбиения τ мелкости ∣τ∣<δ  справедливо неравенство: ∣στ−I∣<ε  или  I−ε<στ<I+ε , отсюда при ∣τ∣<δ  по третьему свойству сумм Дарбу получено неравенство:  I−ε<sτ≤Sτ<I+ε (2.3). Если ∣τ∣<δ , то 0≤Sτ−sτ≤2ε , что  равносильно выполнению условия (2.2).  Достаточность. Пусть f ограничена и выполняется условие (2.1). Из определения нижнего и верхнего интеграла Дарбу и в силу свойства I*≤I* (свойство 4) им: sτ≤I*≤I*≤Sτ . Поэтому 0≤I*−I*≤Sτ−sτ , отсюда в силу (2.1) I*−I*=0 . Обозначим общее значение интегралов Дарбу I*=I*=I, из (2.3) получим: sτ≤I≤Sτ  и поэт. 0≤I−sτ≤Sτ−sτ и 0≤Sτ−I≤Sτ−sτ . В силу (2.1): lim∣τ∣→0(I−sτ)=lim∣τ∣→0(Sτ−I)=0 , значитlim∣τ∣→0sτ=lim∣τ∣→0Sτ=I, но в силу свойства 3 sτ≤στ≤Sτ  (2.4), тогда по теореме о пределе промежуточной функции lim∣τ∣→0στ=I, что и означает интегрируемость функции f. Ч.и т.д.

 Следствия.  1. Если f интегрируема, то не только ее интегральные суммы Римана, но и ее интегральные суммы Дарбу стремятся к ее интегралу при стремлении мелкости  разбиения к 0. 2. Для того, чтобы ограниченная на некотором отрезке функция f была интегрируема на нем необходимо и достаточно lim∣τ∣→0∑ki=1ωi(f)Δxi=0, где ωi(f) колебание функциии на [xi−1,xi] разбиения τ={xi}i=ki=0 отрезка [a,b](это следует из 4 свойства сумм Дарбу).

 

Необходимое условие интегрируемости. Теорема. Если функция интегрируема на отрезке, то она ограничена на нем.  Доказательство. (от противного) Интегрируемая на [a,b] функция f не ограничена и зафиксируем некоторое разбиение τ={xi}i=ki=0. В силу неограниченности f на [a,b] она будет по крайней мере неограниченной на одном отрезке разбиения τ, например, на [x0,x1], тогда на этом отрезке существует последовательность ξ1n∈[x0,x1],n=1,∞  такая, что limn→∞ξ1n=∞ ,limn→∞f(ξ1n)=∞ (1.1). Зафиксируем точки ξi∈[xi−1,xi],i=2,k, тогда сумма ∑ki=2f(ξi)Δxiбудет иметь вполне определенное значение, поэтому в силу (1.1): limn→∞στ(f,ξ,1...,ξ)k=limn→∞(f(ξ1n)Δx1+∑ki=2f(ξi)Δxi)=∞ и значит каково бы ни было М>0 всегда можно подобрать номер n0, что если на первом отрезке [x0,x1] взять точкуξ1n0получим: ∣ ∣  στ(f,ξ1n0,ξ2,...,ξk)∣ ∣  >M, => суммы στ не могут стремиться к конечному пределу при мелкости разбиения δτ=∣τ∣→0 . Действительно, если бы существовал конечный предел lim∣τ∣→0στ=A, то для любогоε>0 нашлось бы такое δ(ε)>0, что для разбиения τ={xi}i=ki=0 отрезка [a,b] мелкости ∣τ∣<δ(ε)  при любом выборе точек ξi∈[xi−1,xi],i=1,k, ∣στ−A∣<ε  и =>∣στ∣=∣(στ−A)+A∣≤∣στ−A∣+∣A∣<ε+∣A∣ . В случае  неограниченности функции f для любого разбиения τ (в т.ч. и для такого, что∣τ∣<δ(ε))  при  любом фиксированном ε>0 можно так выбрать ξi, что выполняется неравенство ∣στ∣>∣A∣+ε . Это противоречие доказывает теорему. Ч.и.т.д. Условие ограниченности функции f необходимое, но НЕ является достаточным. Например, для функции Дирихле: D(x) на [0,1]. Она ограничена, но не интегрируема, т.к. для любого разбиения интегрируемые суммы στ стремятся к 1 если выбрать ξi  рациональными, и к 0 если иррациональными, то есть не стремятся ни к какому пределу.