Басов3

По условию теоремы в области G для функции f(x; y) выполняется локальное условие Липшица. А значит, по лемме о связи между локальным и глобальным условиями Липшица f 2 Lipgly (H); и L –

глобальная константа Липшица, обслуживающая компакт H:

jjy(x) ye(x)jj 0:

21

§4. ПРОДОЛЖЕНИЕ РЕШЕНИЙ

10: Условия продолжения за границу интервала.

Рассмотрим нормальную систему (3.1) y0 = f(x; y) с f 2 C(G): Пусть y = '(x) решение системы, определенное на отрезке [a; b]: Поскольку по определению решения точка (b; '(b)) 2 G; то '(x) может быть продолжено вправо за точку b на полуотрезок Пеано, построенный в точке b (аналогично влево за точку a): И т. д.

При этом иногда можно таким образом продвинуться далеко, в том числе и до бесконечности, а иногда нет.

Разберемся, от чего это зависит.

В примере 1 §1, Гл.I уравнение y0 = y2 имеет, например, решение y = (1 x) 1 задачи Коши с начальными данными x0 = 0; y0 = 1: Влево оно продолжимо до 1; а вправо только до единицы.

Лемма (о продолжении решения за интервал). Пусть y = '(x)

решение системы (3.1), определенное на интервале (a; b):

Для того чтобы оно могло быть продолжено вправо за точку b

Д о к а з а т е л ь с т в о .

Достаточность. Предположим, что решение может быть продолжено вправо за точку b: Значит, существует такое решение y =

(a;b)

(x); определенное на интервале (a; b1) с b1 > b; что (x) '(x):

Поскольку функция y = (x) непрерывна, то (b) = = lim (x);

x!b

т. е. = lim '(x): Кроме того, по определению решения точки

x!b

(x; (x)) 2 G при x 2 (a; b1): В частности точка (b; ) 2 G:

Необходимость. По условию существует lim '(x) = : Доопре-

x!b

делим функцию '(x) в точку b; положив '(b) = ; и проверим, что y = '(x) является решением системы (3.1), определенным на

промежутке (a; b]: Поскольку '(x) = '(x0) + R x f(s; '(s)) ds для

x0

8 x; x0 2 (a; b) и точка (b; ) 2 G; функция f определена и непрерывна в этой точке. Перейдем в последнем равенстве к пределу при x ! b ; который, очевидно, существует, а значит, равенство справедливо и при x = b: Тогда по лемме о продолжении решения за границу отрезка '(x) может быть продолжено вправо за точку b:

22

Df. Интервал ( ; ) называется максимальным интервалом существования решения y = '(x) системы (3.1), если это решение определено на ( ; ) и не может быть продолжено ни на какой промежуток, содержащий ( ; ) внутри себя.

Df. Интегральной кривой системы (3.1) называется график любого ее решения y = '(x); определенного на максимальном интервале существования ( ; ):

Иными словами, интегральная кривая это множество точек

(x) = f(x; '(x)) j x 2 ( ; )g 2 G:

Акак ведет себя интегральная кривая при x ! или x ! ?

20: Поведение решений вблизи границ максимального интервала существования.

Теорема (о поведении интегральной кривой при стремлении аргумента решения к границе максимального интервала существования). Пусть в системе (3.1) f(x; y) 2 C(G); тогда при стремлении аргумента любого решения к границе своего максимального интервала существования интегральная кривая стремится к границе области G; т. е. покидает любой компакт H G и никогда

внего не возвращается.

До к а з а т е л ь с т в о . Пусть y = '(x) – произвольное решение системы (3.1), определенное на максимальном интервале существования ( ; ): Надо показать, что для 8 H G найдется такое 2 ( ; ); что для 8 x 2 ( ; ) точки (x; '(x)) интегральной кривой (x) лежат в множестве GnH: Или, другими словами,

8 H G; 8 fxkg1k=1 2 ( ; ) : xk ! ) 9K > 0 : 8 k > K ) k = (xk; '(xk)) 2 GnH:

Доказывая от противного, предположим, что

9 H1 G; 9 fxkg1k=1; xk ! : 8 k 2 N ) k 2 H1:

Отсюда сразу же вытекает важнейшее утверждение о том, что< +1; так как в противном случае последовательность xk оказывается неограниченной, и найдется индекс k такой, что точкаk интегральной кривой (x) будет лежать вне компакта H1:

23

Возьмем теперь любой компакт H2 такой, что H1 & H2 G:

Это значит, что если 1; 2 – границы H1; H2; то d = ( 1; 2) > 0; где расстояние ( 1; 2) = min8 2 1; 8 2 2fjj jjg:

Покажем, что при x ! интегральная кривая (x) покидает компакт H2 хотя бы один раз.

В противном случае (второй раз "от противного")

8 x0 2 ( ; ); 8 x 2 [x0; ) ) (x) 2 H2:

Покажем, что при таком предположении решение y = '(x) можно продолжить вправо за границу максимального интервала суще-

ствования ; для чего установим существование lim '(x) = :

x!

Если допустить, что такой предел отсутствует (в третий раз "от противного"), то найдутся такие последовательности аргумен-

компакт содержит все свои предельные точки.

Мы попали в условие леммы о продолжении решения за интервал, согласно которой ( ; ) не будет являться максимальным интервалом существования для решения y = '(x): !!!

Следовательно (x) покидает компакт H2 хотя бы один раз, т. е.

9 2 [x0; ) : ( ; '( )) 62H2:

24

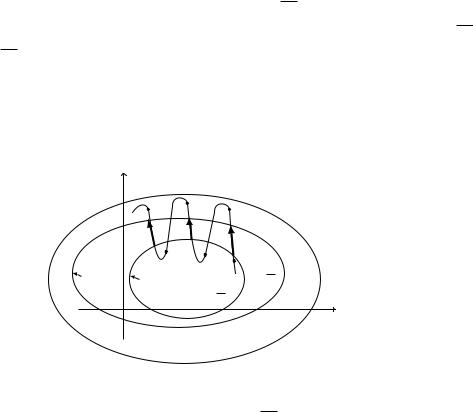
Поскольку x0 – произвольная точка из ( ; ); для 8 k 1 рассмотрим последовательность точек xk0 = ( )=(k + 1); лежащую в ( ; ) и стремящуюся к :

По доказанному выше существует f kg1k=1

( k ! при k ! 1) и ~k = ( k; '( k)) 62H2 для 8 k 1:

Разряжая при необходимости точки последовательностей xk 2 H1

и k 2 GnH2; перенумеруем их так, чтобы они чередовались:

x1 < 1 < x2 < 2 < x3 < : : : ;

и для 8 k 1 рассмотрим интервалы (xk; k):

Существуют моменты t1k; t2k 2 (xk; k) такие, что (tik; '(tik)) 2 i

идля 8 x 2 (t1k; t2k) точка (x; '(x)) 2 H2nH1:

Оценим длину промежутков t2k t1k:

По построению jj(t2k; '(t2k)) (t1k; '(t1k))jj d > 0 или по определению нормы maxft2k t1k; j'1(t2k)) '1(t1k))j; : : : ; j'n(t2k)) 'n(t1k))g d:

Следовательно или t2k t1k > d; или существует индекс j такой,

t2k

P

Рассуждения для левого конца интервала ( ; ) аналогичны.

25

Следствие. Пусть G = (a; b) D; где D – область фазового пространства Rn: Тогда либо решение y = '(x) системы (3.1) определено на всем интервале (a; b); либо при стремлении аргумента x к границе максимального интервала существования его интегральная кривая покидает любой компакт D1 D и никогда

внего не возвращается.

До к а з а т е л ь с т в о . Если, например, у максимального интервала существования ( ; ) решения y = '(x) правый конец< b; то конечно. Если допустить, что найдется D1 D; что

'(x) 2 D1 для 8x 2 [x0; ); то (x; '(x)) 2 [x0; ] D1 G: !!!

30: Продолжимость решений почти линейных систем.

Каждое из решений произвольной нормальной системы (3.1) может быть определено, вообще говоря, на своем максимальном интервале существования, которые не обязательно совпадают и даже имеют общие точки. Но существует класс систем, имеющих общий максимальный интервал существования для всех решений.

Df. Система (3.1) называется почти линейной, если функция f(x; y) 2 C(G); где область G = (a; b) Rn; и существуют непрерывные и неотрицательные на (a; b) функции L(x); M(x) такие, что jjf(x; y)jj L(x) + M(x)jjyjj для 8 (x; y) 2 G:

Теорема (о продолжимости решений почти линейных систем).

Любое решение почти линейной системы продолжимо на (a; b):

Д о к а з а т е л ь с т в о . Рассмотрим произвольное решение почти линейной системы y = '(x); заданное на максимальном

26

В. В. Басов Курс лекций по ОДУ

§5. ЛИНЕЙНЫЕ СИСТЕМЫ. ВВЕДЕНИЕ

10: Существование и единственность решений.

Df. Система (3.1) называется линейной, если она имеет вид

функции pij(x) и qi(x) непрерывны на (a; b):

Таким образом, система (3.1) – линейная, если f = P (x)y + q(x); а область G = (a; b) Rn:

Df. Линейная система (3.14) называется однородной (ЛОС), если

(a;b)

в ней q(x) 0; в противном случае линейная система – неоднородная (ЛНС). Функция q(x) – неоднородность системы (3.14).

Очевидно, что ЛОС всегда имеет тривиальное решение y(x) 0:

Df. Линейная система (3.14) называется вещественной, если все функции pij(x); qi(x) принимают только вещественные значения.

В дальнейшем, если не оговорено противное, будут рассматриваться только вещественные линейные системы.

Исходя из структуры области G; начальные данные для задачи Коши – это произвольная точка x0 из интервала (a; b) и произвольный вектор y0 = (y10; : : : ; yn0) из пространства Rn:

Теорема (о существовании и единственности решений линейных систем). Для любой точки x0 2 (a; b) и для любого вектора y0 2 Rn существует и единственно решение задачи Коши линейной системы (3.14) с начальными данными x0; y0; определенное на некотором отрезке Пеано Ph(x0; y0):

справедлива теорема о существовании и единственности решений нормальной системы (3.1).

27

20: Продолжимость решений линейных систем.

Теорема (о продолжимости решений линейных систем). Любое решение линейной системы (3.14) продолжимо на (a; b):

тогда функции p0(x); q0(x) непрерывны на (a; b):

Оценим сверху компоненты правой части системы (3.14). Имеем:

т. е. система (3.14) почти линейна и любое ее решение продолжимо на (a; b):

30: Комплексные линейные системы.

Если в линейной системе (3.14) pij(x) и qi(x) – комплекснозначные функции вещественного аргумента x; то решение системы (3.14) y = y(x) также будет иметь комплексные значения.

Возникает естественный вопрос о существовании, единственности и продолжимости такого решения.

Пусть y = u(x) + iv(x); P = R(x) + iS(x); q = g(x) + ih(x):

Согласно определению решения, подставляя y(x) в систему (3.14), получаем тождество на интервале (a; b)

u0 + iv0 (R + iS)(u + iv) + g + ih:

Выделяя в нем вещественную и мнимую части, заключаем, что вектор функция (u(x); v(x)) удовлетворяет вещественной линейной системе из 2n уравнений с 2n неизвестными

u0 Ru Sv + g; v0 Su + Rv + h;

к которой можно применить теоремы о существовании и единственности и продолжимости решений.

Таким образом доказано, что решение линейной системы (3.14) с непрерывными на (a; b) комплексными коэффициентами существует, единственно и продолжимо на весь интервал (a; b):

28

§6. ЗАВИСИМОСТЬ РЕШЕНИЙ ОТ НАЧАЛЬНЫХ ДАННЫХ И ПАРАМЕТРОВ

10: Непрерывность решений по начальным данным и параметрам.

Рассмотрим нормальную систему (3.1), зависящую от векторного

где функция f(x; y; ) непрерывна в области F = G M Rn+m; область изменения параметров M = f j jj 0jj < cg:

Фактически, (3.15) представляет собой семейство систем, каждая из которых отвечает своему значению вектора параметров :

Особое место в указанной семействе занимает расчетная система

которая в той или иной форме интегрируется и ее решение поставленной задачи Коши определяет расчетное движение материальной точки в пространственно-временном континууме.

Реальное движение материальной точки, естественно, будет отличаться от расчетного не только из-за погрешностей счета, но и за счет различий между реальными и расчетными значениями начальных данных и параметров как в момент начала, так и в процессе самого движения.

Поэтому основополагающая задача заключается в установлении непрерывной зависимости решений от начальных данных и параметров. В противном случае реальное движение со временем может начать катастрофически отличаться от расчетного.

Приведенные рассуждения вынуждают рассматривать решения зависящими не только от независимой переменной x; но и от начальных данных x0; y0 и вектора параметров :

Иными словами, решение y = y(x; x0; y0; ); причем по определению y(x0; x0; y0; ) = y0( ); т. е. эта запись задает решение задачи Коши с начальными данными x0; y0; а y0; вообще говоря, может непрерывно зависеть от :

29

Теорема (об интегральной непрерывности). Пусть в системе (3.15) функция f(x; y; ) определена, непрерывна и удовлетворяет условию Липшица по y локально в области F = G M пространства точек (x; y; ): И пусть y = '(x) = '(x; 0) есть решение системы (3:150); определенное на отрезке [a; b]: Тогда для системы (3.15) существуют число > 0 и область начальных данных

U = f(x0; y0; ) j a < x0 < b; jjy0 '(x0)jj < ; jj 0jj < g такие, что для любой точки (x0; y0; ) 2 U решение y = y(x; x0; y0; )

определено для 8x 2 [a; b] и является является непрерывной функцией по совокупности своих аргументов в области V = (a; b) U

(эту теорему называют также теоремой о непрерывной зависимости решений от начальных данных и параметров).

Д о к а з а т е л ь с т в о . Существует > 0 такое, что компакт

U = f(x; y; ) j a x b; jjy '(x)jj ; jj 0jj < g F:

По сути, U – это трубчатая -окрестность решения y = '(x; 0): Будем доказывать наличие столь малой константы > 0; что любое решение y = y(x; x0; y0; ) с начальными данными из трубчатой окрестности U продолжимо на [a; b]; непрерывно в V = (a; b) U по совокупности аргументов и его интегральная кривая остается в

компакте U при x 2 [a; b]:

Для этого для любой точки (x0; y0; ) из U будем строить решение y = y(x; x0; y0; ) методом последовательных приближений Пикара, по мере необходимости уменьшая ; но так, чтобы в конечном итоге оно оказалось большим нуля.

30