
- •Российский университет дружбы народов
- •Конспект лекций по молекулярной физике для специальностей «физика» и «радиофизика и электроника» Москва 2006
- •Относительная молекулярная масса вещества
- •Молярная масса вещества - масса одного моля, выраженная в килограммах.
- •Молекула из трех и большего числа атомов: (три координаты центра масс и три угла относительно трех взаимно перпендикулярных осей, проходящих через центр масс).
- •Первое начало термодинамики
- •Теплоемкость тела
- •Теплоемкость при постоянном объеме
Первое начало термодинамики
![]() .
(2)
.
(2)
Здесь
под
![]() понимается работа, совершаемая телом.
Бесконечно малое изменение коли-чества
тепла
понимается работа, совершаемая телом.
Бесконечно малое изменение коли-чества
тепла![]() ,
также как и
,
также как и![]() ,
не всегда является полным дифференциалом.
Согласно определению внутренняя энергия
,
не всегда является полным дифференциалом.
Согласно определению внутренняя энергия![]() есть однозначная функция состояния
термодинами-ческой системы. Поэтому ее
бесконечно малое изменение является
полным дифференциа-лом. В круговом
процессе
есть однозначная функция состояния
термодинами-ческой системы. Поэтому ее
бесконечно малое изменение является
полным дифференциа-лом. В круговом
процессе![]() ,
так как
,
так как![]() .
При этом
.
При этом![]() (см.
рис. 2). Значения
(см.
рис. 2). Значения![]() и
и![]() зависят от вида теплового процесса.
зависят от вида теплового процесса.
Первое начало термодинамики (2) является универсальным законом природы. Оно справе-дливо для любых тепловых процессов и любых агрегатных состояний вещества. Ведем еще оду важную физическую величину, необходимую для количественного описания тепловых процессов.
Теплоемкость тела
![]() .
.
Теплоемкость тела зависит от свойств его вещества, от его массы и от вида теплового процесса с помощью которого ему передается тепло. Теплоемкость 1 кг вещества называется его удельной теплоемкостью ([c] = 1 Дж/кгּград), а теплоемкость 1 моля вещества – молярной теплоемкостью ([C] = 1 Дж/мольּград). В зависимости от вида теплового процесса выделяют следующие значения теплоемкости.
Теплоемкость при постоянном объеме
![]() .
.
Теплоемкость при постоянном давлении
![]() .
.
Здесь
введена новая термодинамическая величина
![]() ,
называемаяэнтальпией
,
называемаяэнтальпией
![]() .
.
В
тепловых процессах при постоянном
давлении
![]() .
Поэтому ее еще называюттепловой
функцией.
Энтальпия так же как и внутренняя энергия
является однозначной функцией состояния
термодинамической системы.
.
Поэтому ее еще называюттепловой
функцией.
Энтальпия так же как и внутренняя энергия
является однозначной функцией состояния
термодинамической системы.
Из
первого начала термодинамики следует,
что всегда
![]() .
Рассмотрим значения этих величин для
идеального газа. В этом случае внутренняя
энергия равна полной кинетической
энергии теплового движения молекул.
Тогдадля
одного моля
идеального газа
.
Рассмотрим значения этих величин для
идеального газа. В этом случае внутренняя
энергия равна полной кинетической
энергии теплового движения молекул.
Тогдадля
одного моля
идеального газа
![]() .
.
Отсюда получаем выражения для молярных теплоемкостей
![]() ,
,
![]() ,
,![]() .
.
Последнее соотношение называется уравнением Майера. Оно справедливо только в случае идеального газа. В дальнейшем нам понадобится еще одна важная величина
![]() ,
,
называемая показателем адиабаты. Для идеального газа она, очевидно, равна
![]() .
.
Лекция 4. Тепловые процессы в идеальном газе.
Будем
рассматривать квазистатические тепловые
процессы в идеальном газе, в которых
термодинамические параметры
![]() одинаковы
во всем объеме газа, но при этом они
изменятся со временем. Можно считать,
что в таких процессах во все моменты
времени выполняется уравнение Клапейрона
– Менделеева
одинаковы
во всем объеме газа, но при этом они
изменятся со временем. Можно считать,
что в таких процессах во все моменты
времени выполняется уравнение Клапейрона
– Менделеева
![]() .
.
1.
Изохорический
процесс (![]() ).
).

В
таком процессе
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
2.
Изобарический
процесс (![]() ).
).

Здесь
![]() ,
,![]() ,
,![]() ,
,![]() .
.
3.
Изотермический
процесс (![]() ).
).

В
этом процессе
![]() ,
,
 ,
,
![]() .
.
4.
Адиабатический
процесс (![]() ).
).
Тепловой
процесс с телом, в котором оно не
обменивается теплом с другими телами,
назы-вается адиабатическим.
Из первого начала термодинамики следует,
что в таком процессе
![]() .
Для идеального газа
.
Для идеального газа![]() ,
поэтому при адиабатическом расширении
идеаль-ный газ охлаждается, а при
адиабатическом сжатии – нагревается.
,
поэтому при адиабатическом расширении
идеаль-ный газ охлаждается, а при
адиабатическом сжатии – нагревается.
Для одного моля идеального газа
![]() ,
или
,
или
![]() .
.
Производя интегрирование, получаем
![]() ,
,
![]() .
.
Возводя
последнее выражение в степень
![]() и используя уравнение Майера, приходим
к уравнению
и используя уравнение Майера, приходим
к уравнению
![]() .
.
Это так называемое уравнение Пуассона для адиабатического процесса в идеальном газе. С помощью уравнения Клапейрона - Менделеева его можно представить в следующих формах
![]()

![]() .
.
Из уравнения Пуассона видно, что если из одного и того же начального состояния с идеальным газом производится либо изотермический процесс (изотерма на рис. 4), либо адиабатический процесс (адиабата), то адиабата лежит ниже изотермы.
Типичным примером адиабатического процесса в идеальном газе является звуковая волна, которую мы рассмотрели в курсе механики. В этом случае успевает установиться локальное равновесие, но перенос тепла между областями с разным давление произойти не успевает.
Все рассмотренные выше процессы происходят при постоянной теплоемкости. Можно ввести еще один тип процессов в идеальном газе.
5.
Политропический
процесс (![]() ).
).
Аналогично случаю адиабатического процесса с помощью первого начала термодинамики для такого процесса можно получить уравнение политропы
![]() ,
где
,
где
![]() -показатель
политропы.
-показатель
политропы.
Для
адиабатического процесса
![]() ,
,![]() ,
для изотермического -
,
для изотермического -![]() ,
,![]() ,
для изохорического -
,
для изохорического -![]() ,
,![]() ,
для изобарического -
,
для изобарического -![]() ,
,![]() .
.
Лекция 5. Распределение молекул идеального газа по координатам и скоростям.
1. Идеальный газ во внешнем поле.
Р

![]() ,
перпенди-кулярными потенциальной
внешней силе
,
перпенди-кулярными потенциальной
внешней силе![]() и отстоя-щими друг от друга на расстоянии
и отстоя-щими друг от друга на расстоянии![]() (рис. 1). Ось
(рис. 1). Ось![]() направлена
противоположно силе
направлена
противоположно силе![]() .
Давления газа на верхней и нижней
площадках равны соответственно
.
Давления газа на верхней и нижней
площадках равны соответственно![]() и
и![]() .
Тогда условие равновесия выделенного
объема можно представить в виде
.
Тогда условие равновесия выделенного
объема можно представить в виде
![]() ,
или
,
или
![]() ,
,
где
![]() - потенциальная энергия молекулы газа.
Будем считать, что температура газа
- потенциальная энергия молекулы газа.
Будем считать, что температура газа
![]() постоянна во всем объеме. Из уравнения
Клапейрона
постоянна во всем объеме. Из уравнения
Клапейрона![]() (локальное равновесие) получим
(локальное равновесие) получим
![]() ,
,
![]() .
.
Интегрируя это уравнение, получаем формулу Больцмана для распределения молекул идеального газа по координатам во внешнем потенциальном поле
![]() .
.
Здесь
![]() - концентрация молекул газа в точке
- концентрация молекул газа в точке![]() ,
в которой
,
в которой![]() .
Аналогично для давления
.
Аналогично для давления
![]() .
В поле тяжести
.
В поле тяжести
![]() .
.
Последнее выражение носит название барометрической формулы. На ней основано устрой-ство альтиметра – прибора для определения высоты над поверхностью Земли.
2. Распределение молекул по скоростям.
Мы
уже ввели понятие средней квадратичной
скорости молекул
![]() .
Но молекулы в газе движутся с разными
скоростями и важно определить какая
часть молекул имеет скорости в определенном
интервале значений. Рассмотрим интервал
значений проекции скорости
.
Но молекулы в газе движутся с разными
скоростями и важно определить какая
часть молекул имеет скорости в определенном
интервале значений. Рассмотрим интервал
значений проекции скорости![]() между
между![]() и
и![]() .
Число молекул в единице объема с такими
значениями
.
Число молекул в единице объема с такими
значениями![]() можно представить в виде
можно представить в виде
![]() .
(1)
.
(1)
Функция
![]() в этом выражении называетсяфункцией
распределения по проекции скорости
в этом выражении называетсяфункцией
распределения по проекции скорости
![]() .
.
Вероятностный
смысл
![]() можно пояснить, если переписать выражение
(1) по другому
можно пояснить, если переписать выражение
(1) по другому
![]() .
.
Таким
образом, вероятность того, что проекция
скорости
![]() молекул лежит в интервале от
молекул лежит в интервале от![]() до
до![]() равна
равна![]() .
.
Понятие вероятности вводится при изучении случайных событий различной природы. Дадим простейшее определение вероятности события:
![]() ,
,
где
![]() - число опытов, приводящих к реализации
данного события,
- число опытов, приводящих к реализации
данного события,![]() -
общее число опытов. Например, при
многократном бросании монеты вероятности
выпадения ее каждой стороны
-
общее число опытов. Например, при
многократном бросании монеты вероятности
выпадения ее каждой стороны![]() ,
,![]() .
Сумма этих вероятностей
.
Сумма этих вероятностей![]() .Событие,
вероятность которого равна единице
называетсядостоверным
(оно выполняется всегда). Одна из сторон
монеты обязательно выпадет. Этот простой
пример отражает одну из основных теорем
теории вероятностей.
.Событие,
вероятность которого равна единице
называетсядостоверным
(оно выполняется всегда). Одна из сторон
монеты обязательно выпадет. Этот простой
пример отражает одну из основных теорем
теории вероятностей.
Теорема сложения вероятностей.
Если
![]() - вероятностиисключающих
друг друга событий,
то вероятность того, что осуществится
какое-нибудь одно из них
- вероятностиисключающих
друг друга событий,
то вероятность того, что осуществится
какое-нибудь одно из них
![]() .
.
Имеет место также теорема для вероятности независимых событий. Например, бросание монеты и следующая за этим попытка сдать экзамен.
Теорема умножения вероятностей.
Вероятность совмещения нескольких независимых событий равна произведению вероят-ностей каждого из них в отдельности
![]() .
.
Вычисление средних значений.
Пусть
![]()
![]() -
число наблюдений значения
-
число наблюдений значения![]() случайной величины
случайной величины![]() ,
,![]() -
полное число наблюдений. Тогда среднее
значение величины
-
полное число наблюдений. Тогда среднее
значение величины![]() можно вычислить по формуле
можно вычислить по формуле
![]() ,
,
где
![]() - вероятность того, что величина
- вероятность того, что величина![]() примет значение
примет значение![]() .
Тогдасреднее
значение проекции скорости молекулы
.
Тогдасреднее
значение проекции скорости молекулы
![]() можно представить в виде
можно представить в виде
![]() .
.
Получим
явный вид функции распределения
![]() .
Попадания скоростей молекул в интервалы
.
Попадания скоростей молекул в интервалы![]() ,
,![]() ,
,![]() являются независимыми событиями. Значит
вероятность попадания вектора скорости
являются независимыми событиями. Значит
вероятность попадания вектора скорости![]() сразу в три эти интервала равна
сразу в три эти интервала равна
![]() .
.
Из хаотичности теплового движения молекул вытекает свойство четности функции распределения
![]() ,
или
,
или
![]() .
.
Удобно
ввести переменные
![]() ,
,![]() ,
,![]() .
Тогда для функции распределения по
скоростям справедливы соотношения
.
Тогда для функции распределения по
скоростям справедливы соотношения
![]() .
(2)
.
(2)
Рассмотрим
такие изменения
![]() ,
которые удовлетворяют соотношениям
,
которые удовлетворяют соотношениям![]() ,
,![]() .
Тогда из (2) получим
.
Тогда из (2) получим
![]() (введем
такое обозначение).
(введем
такое обозначение).
Решая это дифференциальное уравнение, находим
![]() .
(3)
.
(3)
Для функции распределения выполняется условие нормировки
![]() ,
,
означающее,
что попадание
![]() в интервал от
в интервал от![]() до
до![]() является достоверным событием. Подставляя
в это условие выражение (3), находим
константу
является достоверным событием. Подставляя
в это условие выражение (3), находим
константу![]()
![]() .
.
Константу
![]() можно найти с помощью равенства
можно найти с помощью равенства
![]() .
.
Проводя
интегрирование, находим
![]() .
Подставляя
.
Подставляя![]() и
и![]() в
выражение (3), получаемраспределение
Максвелла по проекции скорости молекул
на ось
в
выражение (3), получаемраспределение
Максвелла по проекции скорости молекул
на ось
![]()
![]() .
.
С помощью соотношения (2) легко получить функцию распределения по всем проекциям скорости молекул
![]() .
.
Если
газ находится во внешнем потенциальном
поле то можно рассматривать более общее
распределение по полной энергии молекул
![]()
![]() ,
,
называемое распределением Максвелла – Больцмана.
Рассмотрим
распределение молекул по модулю скорости.
Вероятность найти молекулу в пространстве
скоростей в элементе объема
![]() в окрестности скорости
в окрестности скорости![]()
![]() .
.
Для
нахождения вероятности того, что молекула
имеет модуль скорости в интервале от
![]() до
до![]() мы должны в качестве взять в качестве
элементарного объема шаровой слой
радиуса
мы должны в качестве взять в качестве
элементарного объема шаровой слой
радиуса![]() и толщиной
и толщиной![]() .
В этом случае
.
В этом случае![]() ифункция
распределения по модулю скорости
принимает вид
ифункция
распределения по модулю скорости
принимает вид

![]() .
.
Эта
функция имеет максимум при
![]() .
Величина
.
Величина![]() называетсянаивероятнейшей
скоростью молекул
газа (рис. 2). При этом
называетсянаивероятнейшей
скоростью молекул
газа (рис. 2). При этом
![]() .
.
Лекция 6. Экспериментальные подтверждения молекулярно-кинетической теории. Броуновское движение.
Опыт Штерна.
В

![]() .
В случае вращения с угловой скоростью
.
В случае вращения с угловой скоростью![]() молекула, движущаяся со скоростью
молекула, движущаяся со скоростью![]() ,
попадает в точку
,
попадает в точку![]() ,
отстоящую от
,
отстоящую от![]() на расстоянии
на расстоянии
![]() ,
откуда
,
откуда
![]() ,
,![]() .
.
Число
молекул со скоростями от
![]() до
до![]() ,
испускаемых нитью в 1 секунду
,
испускаемых нитью в 1 секунду
 .
.
Проведенные
Штерном измерения толщины слоя осевшего
серебра с большой точностью соответствовали
этому выражению. Значения скоростей
изменялись примерно от 540 м/сек до 640
м/сек, а
![]() 580
м/сек.
580
м/сек.
Распределение Максвелла и атмосферы планет.
При
столкновении молекул в атмосфере планеты
они могут приобретать скорости,
превыша-ющие вторую космическую скорость
![]() .
Такие молекулы покидают атмосферу
планеты (убегающие
молекулы).
Такой процесс называется рассеянием
атмосферы.
Число молекул, покидающих атмосферу в
единицу времени можно определить с
помощью выражения
.
Такие молекулы покидают атмосферу
планеты (убегающие
молекулы).
Такой процесс называется рассеянием
атмосферы.
Число молекул, покидающих атмосферу в
единицу времени можно определить с
помощью выражения
![]() ,
,
где
![]() -
распределение Максвелла по модулю
скорости,
-
распределение Максвелла по модулю
скорости,![]() - площадь поверхности планеты,
- площадь поверхности планеты,![]() -
концентрация молекул у ее поверхности.
Множитель
-
концентрация молекул у ее поверхности.
Множитель![]() появляется после усреднения по всем
углам падения молекул по отношению к
поверхности
появляется после усреднения по всем
углам падения молекул по отношению к
поверхности![]() ,
,![]() -средняя
скорость убегающих молекул
-средняя
скорость убегающих молекул
![]() .
.
Пренебрегая кривизной поверхности планеты, можно оценить полное число молекул в атмосфере по формуле Больцмана
![]() .
.
С помощью приведенных соотношений можно получить уравнение
![]() ,
,
![]() -время
рассеяния атмосферы,
-время
рассеяния атмосферы,
![]() .
.
Для
Земли
![]() км/сек,
км/сек,![]() 9.8
м/сек2
. Отсюда при
9.8
м/сек2
. Отсюда при
![]() 3000К
для атомарного водорода
3000К
для атомарного водорода
![]() 27
лет, а для молекулярного водорода
27
лет, а для молекулярного водорода![]() 2ּ1012
лет.
2ּ1012
лет.
Броуновское движение.
Одним из убедительных доказательств молекулярно-кинетической теории является так называемое броуновское движение, открытое в 1827 г. английским ботаником Броуном.
Он
обнаружил, что при рассмотрении под
микроскопом частицы, взвешенные в
жидкости, находятся в непрерывном
беспорядочном движении. Оно возникает
вследствие ударов со стороны движущихся
молекул жидкости. На основе такого
представления Эйнштейном и Смолуховским
была построена теория броуновского
движения (1906 г.). Ее основные положения
состоят в следующем. Движение крупной
(по сравнению с размером молекул) частицы
массы
![]() в
жидкости можно описать в проекции на
ось
в
жидкости можно описать в проекции на
ось![]() с помощью уравнения
с помощью уравнения
![]() ,
(1)
,
(1)
где
первое слагаемое в правой части
представляет собой силу вязкого трения
по формуле Стокса, а
![]() есть
сила случайных толчков со стороны
молекул жидкости. Назовемподвижностью
частицы
величину
есть
сила случайных толчков со стороны
молекул жидкости. Назовемподвижностью
частицы
величину
![]() .
После несложных преобразований можно
привести уравнение (1) к следующему виду
.
После несложных преобразований можно
привести уравнение (1) к следующему виду
![]() .
(2)
.
(2)
Усредним
уравнение (2) по всем броуновским частицам.
В силу хаотичности движения молекул
![]() .
Так как броуновские частицы находятся
в тепловом равновесии с моле-кулами
жидкости, то
.
Так как броуновские частицы находятся
в тепловом равновесии с моле-кулами
жидкости, то![]() .
При таких предположениях после усреднения
получим
.
При таких предположениях после усреднения
получим
![]() .
.
Решение
этого уравнения имеет вид
![]() и называетсяформулой
Эйнштейна.
Она была экспериментально подтверждена
в опытах Перрена в 1908 г.
и называетсяформулой
Эйнштейна.
Она была экспериментально подтверждена
в опытах Перрена в 1908 г.
Лекция 7. Явления переноса и столкновения молекул в газе.
Переход от неравновесных состояний к равновесным происходит благодаря явлениям переноса. При этом происходит выравнивание значений термодинамических параметров. В зависимости от вида переносимых физических величин можно выделить три явления переноса.
1. Диффузия.
При
диффузии происходит перенос
массы и выравнивание плотности.
Пусть плотность газа
![]() меняется вдоль оси
меняется вдоль оси![]() .
Опытным путем был получензакон
диффузии
.
Опытным путем был получензакон
диффузии
![]() ,
(1)
,
(1)
где
![]() - масса вещества, переносимая через
площадку
- масса вещества, переносимая через
площадку![]() ,
перпендикулярную оси
,
перпендикулярную оси![]() ,
за время
,
за время
![]() .
Коэффициент
.
Коэффициент
![]() называетсякоэффициентом
диффузии,
называетсякоэффициентом
диффузии,
![]() 1
м2/сек.
Знак “-” означает, что перенос массы
происходит в направлении уменьшения
плотности. Величина
1
м2/сек.
Знак “-” означает, что перенос массы
происходит в направлении уменьшения
плотности. Величина
![]() является проекцией градиента плотности
на ось
является проекцией градиента плотности
на ось![]() .
В дальнейшем мы будем называть ее простоградиентом
плотности.
.
В дальнейшем мы будем называть ее простоградиентом
плотности.
2. Теплопроводность.
В
этом процессе происходит перенос
тепла и выравнивание температуры.
При изменении температуры вдоль оси
![]() закон
теплопроводности
имеет вид
закон
теплопроводности
имеет вид
![]() ,
,
где
![]() - количество тепла, переносимого через
площадку
- количество тепла, переносимого через
площадку![]() ,
перпендикулярную оси
,
перпендикулярную оси![]() ,
за время
,
за время
![]() .
Коэффициент
.
Коэффициент
![]() называетсякоэффициентом
теплопроводности,
называетсякоэффициентом
теплопроводности,
![]() 1 Дж/мּсекּград,
1 Дж/мּсекּград,
![]() -градиент
температуры.
-градиент
температуры.
3. Внутреннее трение.
Происходит перенос импульса между слоями газа (жидкости), движущимися друг относи-тельно друга. При этом между слоями возникает сила вязкого трения
![]() ,
,
где
ось
![]() перпендикулярна скорости течения газа
перпендикулярна скорости течения газа![]() ,
,![]() -
площадка слоя газа с коорди-натой
-
площадка слоя газа с коорди-натой![]() ,
,![]() -коэффициент
вязкости,
-коэффициент
вязкости,
![]() 1 кг/мּсек
= 1 г/смּсек
= 1 Пуаз,
1 кг/мּсек
= 1 г/смּсек
= 1 Пуаз,
![]() -градиент
скорости.
-градиент
скорости.
Процессы переноса в газе происходят в результате столкновений молекул. Рассмотрим основные величины, используемые для описания столкновений.
Средняя
длина свободного пробега молекул
![]() – среднее расстояние между двумя
последовательными столкновениями.
– среднее расстояние между двумя
последовательными столкновениями.
Эффективное сечение столкновений.
Е

![]() налетает на другую такую же молекулу,
то они столкнутся, если расстояние между
их центрами не превышает
налетает на другую такую же молекулу,
то они столкнутся, если расстояние между
их центрами не превышает![]() (рис. 1). Площадь заштрихованной окружности
(рис. 1). Площадь заштрихованной окружности![]() называетсяэффективным
сечением столкновений.
называетсяэффективным
сечением столкновений.
Если
центр налетающей молекулы попадает в
заштрихованную площадку
![]() (прицельная
площадь)
, то молекулы сталкиваются. Эффективное
сечение столкновений имеет также
вероятностный смысл. Можно показать,
что величина
(прицельная
площадь)
, то молекулы сталкиваются. Эффективное
сечение столкновений имеет также
вероятностный смысл. Можно показать,
что величина
![]() численно равна вероятности столкновения
молекулы в единице объема.
численно равна вероятности столкновения
молекулы в единице объема.
Число столкновений молекулы за 1секунду
![]() .
(2)
.
(2)

Это
выражение можно получить, рассмотрев
цилиндрический объем с площадью основания
![]() и высотой
и высотой![]() (рис. 2). Здесь
(рис. 2). Здесь![]() - средняя скорость молекул. Очевидно,
молекула в левом основании цилиндра
столкнется со всеми молекулами внутри
выделенного объема. На самом деле, после
каждого столкновения направление
движения выделенной молекулы изменяется
и цилиндр становится лома-ным. Однако,
формула (2) при этом не изменяется.
- средняя скорость молекул. Очевидно,
молекула в левом основании цилиндра
столкнется со всеми молекулами внутри
выделенного объема. На самом деле, после
каждого столкновения направление
движения выделенной молекулы изменяется
и цилиндр становится лома-ным. Однако,
формула (2) при этом не изменяется.
С
помощью (2) можно получить выражение для
длины свободного пробега
![]() .
Очевидно,
.
Очевидно,
![]() .
.
При
получении (1) мы считали молекулы внутри
выделенного цилиндра неподвижными.
Можно уточнить выражение для
![]() ,
если учесть относительное движение
молекул. Легко показать, что средняя
скорость относительного движения
,
если учесть относительное движение
молекул. Легко показать, что средняя
скорость относительного движения![]() .
Отсюда
.
Отсюда
![]() .
(3)
.
(3)
Приведем
характерные значения величин
![]() и
и![]() .
Для воздуха при 00С
и
.
Для воздуха при 00С
и
![]() =
1 атм
=
1 атм![]() см-3
,
см-3
,
![]() см2,
см2,
![]() см.
см.
Как было отмечено выше, явления переноса в газе происходят в результате столкновений молекул. Поэтому коэффициенты переноса должны зависеть от длины свободного пробега и средней скорости молекул. Рассмотрим эту зависимость для процесса диффузии.
Как
и в законе диффузии (1) будем считать,
что плотность газа
![]() меняется вдоль оси
меняется вдоль оси![]() .
.
Рассмотрим
малую площадку
![]() ,
перпендикулярную этой оси . Если бы все
молекулы двигались слева направо со
скоростью
,
перпендикулярную этой оси . Если бы все
молекулы двигались слева направо со
скоростью![]() ,
то через
,
то через![]() за время
за время![]() проходила бы масса газа
проходила бы масса газа![]() .
Пусть
.
Пусть![]() - плотности газа соответственно слева
и справа от площадки на расстоянии
- плотности газа соответственно слева
и справа от площадки на расстоянии![]() .
Тогда в силу того, что в этих промежутках
нет столкновений, слева направо через
.
Тогда в силу того, что в этих промежутках
нет столкновений, слева направо через![]() за время
за время![]() проходит масса
проходит масса
![]() .
.
Множитель
![]() появляется из-за того, что в среднем
появляется из-за того, что в среднем![]() молекул движется вдоль оси
молекул движется вдоль оси![]() и
и![]() от этого количества – слева направо.
от этого количества – слева направо.
Аналогично справа налево проходит масса
![]() .
.
Тогда
полная масса газа, проходящая через
площадку
![]() за время
за время![]()
![]() .
(4)
.
(4)
Пусть
на площадке
![]() значение плотности равно
значение плотности равно![]() .
Тогда в виду малости
.
Тогда в виду малости![]() можно записать
можно записать
![]() ,
,
![]() ,
,![]() .
.
Подставляя последнее выражение в (4), получим
![]() ,
,
![]() .
.
Аналогичным образом можно получить
![]() ,
,
![]() .
.
В
проведенном анализе мы считали молекулы
твердыми шариками радиуса
![]() .
В такой модели из выражения (3) следует
длина свободного пробега не зависит от
температуры. Тогда можно считать, что
.
В такой модели из выражения (3) следует
длина свободного пробега не зависит от
температуры. Тогда можно считать, что![]() или
или![]() .
Средняя скорость молекул идеального
газа
.
Средняя скорость молекул идеального
газа![]() .
Отсюда
.
Отсюда![]() при
при![]() и
и![]() при
при![]() .
Из выражений для
.
Из выражений для![]() и
и![]() следует, что эти коэффициенты переноса
не зависят от
следует, что эти коэффициенты переноса
не зависят от![]() при
при![]() и пропор-циональны
и пропор-циональны![]() при
при![]() .
.
Лекция 8. Нестационарные процессы переноса. Перенос в разреженных газах.
Процессы
переноса называются стационарными,
если градиент соответствующей физичес-кой
величины не зависит от времени. Такой
процесс возможен только при наличии
соответ-ствущих источников. Например,
в процессе стационарной теплопроводности
всегда при-сутствует источник тепла и
некоторые тела, поглощающие тепло. При
этом градиент температуры
![]() не меняется со временем в каждой точке.
Удобно для описания процессов переноса
использовать понятиепотока
соответствующей переносимой величины.
Например, поток
тепла
не меняется со временем в каждой точке.
Удобно для описания процессов переноса
использовать понятиепотока
соответствующей переносимой величины.
Например, поток
тепла
![]() равен количеству тепла, переносимому
в единицу времени через единицу площади
перпендикулярно к направлению градиента
температуры
равен количеству тепла, переносимому
в единицу времени через единицу площади
перпендикулярно к направлению градиента
температуры
![]() .
.
Тогда уравнение теплопроводности можно представить в виде
![]() .
(1)
.
(1)
Отсюда следует, что при стационарной теплопроводности поток тепла в любой плоскости, перпендикулярной к направлению градиента температуры не изменяется со временем.
В нестационарных процессах переноса градиенты физических величин изменяются со временем. При этом, если нет внешних источников, происходит выравнивание этих величин по всему объему. В этом случае важно выяснить, как зависит время установления равнове-сия от параметров физической системы.

Рассмотрим
конкретный процесс нестационарной
теплопроводности. Два сосуда с газом с
объемами
![]() ,
,![]() и начальными температурами
и начальными температурами![]() ,
,![]() соединены трубкой длины
соединены трубкой длины![]() с площадью поперечного сечения
с площадью поперечного сечения![]() (рис. 1). Пусть
(рис. 1). Пусть![]() .
Будем считать, что вдоль трубки температура
изменяется линейно
.
Будем считать, что вдоль трубки температура
изменяется линейно
![]() ,
где
,
где
![]() .
.
За
время
![]() из одного сосуда в другой перейдет
количество тепла
из одного сосуда в другой перейдет
количество тепла
![]() .
.
При
этом в сосуде 1 температура уменьшится
на
![]() , а в сосуде 2 – увеличится на
, а в сосуде 2 – увеличится на![]() .
Пусть плотность газа равна
.
Пусть плотность газа равна![]() ,
а его удельная теплоемкость при постоянном
объеме равна
,
а его удельная теплоемкость при постоянном
объеме равна![]() .
Тогда изменения температуры газа в
сосудах можно представить в виде
.
Тогда изменения температуры газа в
сосудах можно представить в виде
![]() .
.
Тогда
изменение разности температур
![]() за время
за время![]()
![]() .
.
Таким
образом, мы пришли к дифференциальному
уравнению для
![]() :
:
![]() ,
где
,
где
![]() -постоянная
времени теплопроводности
,
-постоянная
времени теплопроводности
,
![]() -
-
приведенный объем. Решение этого уравнения имеет вид
![]() ,
,
![]() - начальная разность температур газа в
сосудах.
- начальная разность температур газа в
сосудах.
Следовательно,
постоянная времени теплопроводности
![]() равна характерному времени выравнивания
температуры. В выражении для
равна характерному времени выравнивания
температуры. В выражении для![]() удобно выделить сомножитель, зависящий
только от свойств газа
удобно выделить сомножитель, зависящий
только от свойств газа
![]() ,
называемый коэффициентом
температуропроводности.
,
называемый коэффициентом
температуропроводности.
Аналогичным образом можно рассмотреть процесс нестационарной диффузии. В этом случае процесс выравнивания плотности определяется постоянной времени диффузии
![]() .
.
Общее уравнение нестационарной теплопроводности.

Рассмотрим
изменение количества тепла в малом
объеме, заключенном между двумя площадками
![]() перпендикулярными оси
перпендикулярными оси![]() и отстоящими слева и справа от точки
и отстоящими слева и справа от точки![]() на расстоянии
на расстоянии![]() (рис. 2). Будем также как и выше считать,
что поток тепла имеет место только вдоль
оси
(рис. 2). Будем также как и выше считать,
что поток тепла имеет место только вдоль
оси![]() .
Тогда изменение количества тепла в
объеме
.
Тогда изменение количества тепла в
объеме![]() за время
за время![]() равно
равно
![]() .
.
С
помощью разложения
![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки![]() ,
а также используя уравнение (1), получим
,
а также используя уравнение (1), получим
![]() .
.
С
другой стороны можно вычислить
![]() через теплоемкость и изменение температуры
через теплоемкость и изменение температуры
![]()
Поделив
два последних уравнения на
![]() и перейдя к пределу при
и перейдя к пределу при![]() ,
получимуравнение
теплопроводности
,
получимуравнение
теплопроводности
![]() .
.
Явления переноса в разреженных газах.
Разреженный
газ (вакуум)
– длина свободного пробега молекул
![]() сравнима или больше, чем характерный
размер сосуда
сравнима или больше, чем характерный
размер сосуда![]() ,
в котором находится газ, то есть
,
в котором находится газ, то есть![]() .
В этом случае роль длины свободного
начинает выполнять среднее расстояние
между ударами о стенки и при вычислении
коэффициентов переноса можно положить
.
В этом случае роль длины свободного
начинает выполнять среднее расстояние
между ударами о стенки и при вычислении
коэффициентов переноса можно положить![]() .
.
Теплопроводность в разреженном газе.
Для
идеального газа в обычных условиях
(лекция 7)
![]() .
В разреженном газе
.
В разреженном газе![]() ,
поэтому плотность не сокращается за
счет зависимости
,
поэтому плотность не сокращается за
счет зависимости![]() и возникает линейная зависи-мость
и возникает линейная зависи-мость![]() от давления газа
от давления газа
![]() (
(![]() - масса молекулы газа), то есть
- масса молекулы газа), то есть![]() .
.
Такая зависимость реализуется в сосудах с двойными стенками, между которыми находится разреженный газ (сосуд Дьюара, термос). Чем меньше давление разреженного газа тем меньше теплопроводность стенок такого сосуда.
Вытекание разреженного газа через малое отверстие (эффузия).
Отверстие
считаем малым, если его диаметр
![]() .
Тогда скорость вытекания молекул газа
.
Тогда скорость вытекания молекул газа
![]() .
(2)
.
(2)
Если при этом в сосуде находится смесь газов, то быстрее вытекает более легкая компо-нента. Это явление используется для разделения изотопов.
Эффект Кнудсена.
Если
два сосуда с газом соединены тонкой
трубкой с диаметром
![]() ,
то при равновесии
,
то при равновесии
![]() .
Тогда из (2) следует связь между давлениями
и температурами
.
Тогда из (2) следует связь между давлениями
и температурами
![]() .
.
Лекция 9. Тепловые машины. Теоремы Карно.
Из опыта известно, что работу можно произвести только с помощью тел, не находящихся в тепловом равновесии. Но если просто соединить два тела с разными температурами, то система через некоторое время придет к состоянию равновесия и мы в дальнейшем не получим никакой работы. Чтобы вернуть систему в первоначальное состояние, мы должны произвести некоторые изменения в данной системе и в окружающих телах. В связи с этим возникает важное понятие обратимости и необратимости тепловых процессов.
Обратимые процессы.
Процесс в термодинамической системе называется обратимым, если возможно осуществить его в обратном порядке, проходя через все его промежуточные состояния без изменения состояния внешних тел.
Так как каждое состояние в квазистатическом процессе является равновесным, то такой процесс можно считать обратимым.
Необратимые процессы.
Если для данного процесса невозможен обратный процесс без изменения во внешних телах, то он называется необратимым.
Все процессы, сопровождающиеся теплопередачей от нагретого тела к менее нагретому являются необратимыми. Существует много других необратимых процессов, которые мы рассмотрим в дальнейшем.
Тепловая машина.
Л

![]() и отдает охладителю теплоту
и отдает охладителю теплоту![]() .
За каждый цикл совершается работа
.
За каждый цикл совершается работа![]() .
Здесь
.
Здесь![]() ,
,![]() .
Эффективность работы тепловой машины
характеризуетсякоэффициентом
полезного действия (к.п.д.)
.
Эффективность работы тепловой машины
характеризуетсякоэффициентом
полезного действия (к.п.д.)
![]()
Из сказанного выше можно заключить, что с помощью тепловой машины можно получить максимально возможную работу, если тепловые процессы в ней происходят обратимым образом. На практике это невозможно, так как всегда имеет место контакт тел с разными температурами. Для вычисления максимально возможной работы следует рассмотреть идеальную тепловую машину, в которой все процессы обратимы.

Идеальная тепловая машина. Цикл Карно.
В
идеальной тепловой машине рабочим телом
являет-ся идеальный газ. С рабочим телом
в каждом цикле про-изводится обратимый
круговой процесс, назы-ваемый циклом
Карно (рис. 2). Он состоит из двух изотерм
(![]() и
и![]() )
и двух адиабат (
)
и двух адиабат (![]() и
и![]() ).
На участке
).
На участке![]() рабочее
тело получает тепло от нагрева-теля, а
на участке
рабочее
тело получает тепло от нагрева-теля, а
на участке![]() –
отдает тепло охладителю.
–
отдает тепло охладителю.
Для
вычисления к.п.д. достаточно вычислить
работы
![]() и
и![]() на изотермах. Работа газа на изотерме
на изотермах. Работа газа на изотерме![]()
![]() .
.
Из
уравнения Пуассона для адиабаты
![]() следует, что
следует, что .
Аналогично для
.
Аналогично для![]() получим
получим
![]() ,
где
,
где
 .
.
Учитывая,
что на изотермах
![]() и
и![]() отсюда можно получитьформулу
Карно
для к.п.д. идеальной тепловой машины
отсюда можно получитьформулу
Карно
для к.п.д. идеальной тепловой машины
![]() .
.
Имеют место следующие фундаментальные теоремы Карно.
Теорема 1.
К.п.д. тепловой машины, работающей при данных значениях температур нагревателя и охладителя, не может быть больше, чем к.п.д. машины, работающей по обратимому циклу Карно при тех же температурах нагревателя и охладителя.
Теорема 2.
К.п.д. идеальной тепловой машины не зависит от рабочего тела, а определяется лишь температурами нагревателя и охладителя.
Лекция 10. Второе начало термодинамики. Энтропия.
Теоремы Карно явились основой для формулировки второго начала термодинамики (или второго закона термодинамики). Этот фундаментальный закон природы позволяет количест-венно описать направленность процессов в термодинамических системах. Из него также следует ряд общих термодинамических соотношений, справедливых для любого состояния вещества. Существует несколько различных формулировок этого закона.
Первая формулировка второго начала термодинамики (принцип Томсона).
Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара.
Если бы такой процесс был возможен, то это означало бы возможность вечного двигателя второго рода, который мог бы непрерывно совершать работу, поглощая, например, теплоту от нагретой Солнцем океанской воды. При этом, в отличие от широко известного вечного двигателя первого рода, закон сохранения энергии не нарушался бы.
Можно записать выражение для к.п.д. цикла Карно в виде
![]() ,
или
,
или
![]() .
.
Последнее соотношение представляет собой частный случай равенства Клаузиуса для произвольного обратимого кругового процесса
![]() .
.
По первой теореме Карно для тепловой машины с необратимым круговым процессом
![]() ,
то есть
,
то есть
![]() .
.
В общем случае необратимого кругового процесса имеет место неравенство Клаузиуса
![]() .
.
Эти соотношения в дальнейшем привели к понятию одной из важнейших физических величин – энтропии.
Для бесконечно малого обратимого изменения состояния термодинамической системы изменение ее энтропии определяется как
![]() .
.
При
этом
![]() является полным дифференциалом. Это
следует из равенства Клаузиуса, так как
при возвращении в исходное состояние
энтропия остается неизменной независимо
от конкретного вида кругового процесса.
Отсюда, в частности, вытекает еще одна
формули-ровка второго начала термодинамики.
является полным дифференциалом. Это
следует из равенства Клаузиуса, так как
при возвращении в исходное состояние
энтропия остается неизменной независимо
от конкретного вида кругового процесса.
Отсюда, в частности, вытекает еще одна
формули-ровка второго начала термодинамики.
Вторая формулировка второго начала термодинамики.
Энтропия термодинамической системы, находящейся в равновесном состоянии, является однозначной функцией этого состояния.
Рассмотрим
изменение энтропии замкнутой
термодинамической системы. Очевидно,
в обра-тимых процессах
![]() ,
так как в этом случае суммарное малое
изменение
,
так как в этом случае суммарное малое
изменение![]() .
.

Для того, чтобы определить, как изменяется энтропия в необратимых процессах, рассмотрим круговой процесс, состоящий из необратимого процесса 1 – 2 и обратимого процесса 2 – 1 (рис. 1). При этом на этапе 1 – 2 система является замкнутой, а на этапе 2 – 1 – незамкнутой. Тогда для полного кругового необратимого процесса выпол-няется неравенство Клаузиуса
![]() .
.
Так процесс 2 – 1 является обратимым, то отсюда получим
![]() .
.
На
этапе 1 – 2 система является замкнутой,
поэтому здесь
![]() .
Таким образом измене-ние энтропии
замкнутой системы в необратимом процессе
.
Таким образом измене-ние энтропии
замкнутой системы в необратимом процессе
![]() .
.
Отсюда вытекает третья формулировка второго начала.
Третья формулировка второго начала термодинамики.
Энтропия замкнутой термодинамической системы не убывает при любых происходящих в ней процессах. В необратимых процессах она возрастает, а в обратимых – остается неизмен-ной.
Энтропия одного моля идеального газа.
Первое начало термодинамики для одного моля идеального газа в бесконечно малом обратимом процессе можно записать в виде
![]() .
.
Отсюда получаем
![]() ,
,
![]() .
.
В
силу того, что энтропия является
аддитивной величиной (пропорциональна
массе) для
![]() молей идеального газа
молей идеального газа
![]() .
(1)
.
(1)
В силу дифференциального характера определения энтропии, она так же как и потенциаль-ная энергия в механике, определена с точностью до произвольной константы.
Вычислим изменение энтропии в конкретных необратимых процессах с идеальным газом.
1. Расширение газа в вакуум.
Р

![]() ,
,![]() (теплоизоляция)
и из первого начала термодинамики
следует, что
(теплоизоляция)
и из первого начала термодинамики
следует, что![]() .
Для идеального газа при этом
.
Для идеального газа при этом![]() .
Тогда изменение энтропии одного моля
идеального газа в таком процессе
.
Тогда изменение энтропии одного моля
идеального газа в таком процессе
![]() ,
,
то
есть процесс является необратимым.
Мы можем пользоваться выражением (1) для
энтро-пии в силу того, что начальное и
конечное состояния являются равновесными.
При этом, однако, нужно убедиться в том,
что существует обратимый процесс,
переводящий систему из начального
состояния в конечное. В данном случае
таким процессом является изотерми-ческий
процесс с расширением газа от объема
![]() до объема
до объема![]() .
При этом к газу нужно подводить тепло,
то есть система станет незамкнутой.
Укажем на возможное ошибочное решение
данной задачи. Из условия теплоизоляции
.
При этом к газу нужно подводить тепло,
то есть система станет незамкнутой.
Укажем на возможное ошибочное решение
данной задачи. Из условия теплоизоляции![]() и по определению энтропии
и по определению энтропии![]() и
и![]() .
Ошибка состоит в том, что к необратимому
процессу в целом опреде-ление энтропии
неприменимо.
.
Ошибка состоит в том, что к необратимому
процессу в целом опреде-ление энтропии
неприменимо.
2. Смешивание газов. Парадокс Гиббса.
Пусть
при тех же условиях, что и в предыдущем
случае в левой части сосуда находится
![]() молей газа 1, а в правой с объемом
молей газа 1, а в правой с объемом![]() –
–![]() молей газа 2. После открытия перегородки
газы перемешиваются и в конце получается
равновесная смесь газов. Полное изменение
энтропии
молей газа 2. После открытия перегородки
газы перемешиваются и в конце получается
равновесная смесь газов. Полное изменение
энтропии
![]() .
.
Следовательно,
такой процесс является необратимым.
Парадокс
Гиббса
состоит в том, что если газы 1 и 2 одинаковы,
то по этой формуле также будет
![]() ,
хотя в этом случае конечное состояние
не отличается от начального. Ошибочность
этого результата объясняет-ся
невозможностью для одинаковых газов
обратимым образом перевести систему
из началь-ного состояния в конечное. В
случае разных газов такой процесс
возможен. Для этого пере-городку нужно
составить из двух полупрозрачных
перегородок
,
хотя в этом случае конечное состояние
не отличается от начального. Ошибочность
этого результата объясняет-ся
невозможностью для одинаковых газов
обратимым образом перевести систему
из началь-ного состояния в конечное. В
случае разных газов такой процесс
возможен. Для этого пере-городку нужно
составить из двух полупрозрачных
перегородок![]() и
и![]() ,
причем
,
причем![]() пропу-скает только газ 1, а
пропу-скает только газ 1, а![]() -
только газ 2. Медленно перемещая сначала
перегородку
-
только газ 2. Медленно перемещая сначала
перегородку![]() ,
а затем перегородку
,
а затем перегородку![]() до стенок сосуда мы обратимым образом
переведем систему в конечное состояние.
до стенок сосуда мы обратимым образом
переведем систему в конечное состояние.
Лекция 11. Флуктуации. Статистический смысл энтропии.
Второе
начало термодинамики говорит о том, что
все процессы в замкнутых системах идут
в сторону возрастания энтропии. При
достижении значения
![]() система приходит к состоя-нию
термодинамического равновесия и все
процессы в ней прекращаются. Однако, в
силу хаотичности теплового движения и
конечности числа частиц в системе
равновесие имеет динамический характер.
система приходит к состоя-нию
термодинамического равновесия и все
процессы в ней прекращаются. Однако, в
силу хаотичности теплового движения и
конечности числа частиц в системе
равновесие имеет динамический характер.
Флуктуации – самопроизвольные отклонения физических величин от их средних значений, обусловленные тепловым движением молекул.
Например,
если мысленно разделить сосуд с газом
на две части, то в каждой части в состоя-нии
равновесия будут свои средние числа
частиц
![]() и
и![]() .
Тогда флуктуации числа час-тиц в данный
момент времени равны
.
Тогда флуктуации числа час-тиц в данный
момент времени равны
![]() ,
,
![]() .
.
Относительная
флуктуация
числа частиц
![]() уменьшается с ростом числа частиц в
сис-теме. В принципе возможна такая
флуктуация, при которой все частицы
окажутся в одной части сосуда. При
большом числе частиц вероятность
уменьшается с ростом числа частиц в
сис-теме. В принципе возможна такая
флуктуация, при которой все частицы
окажутся в одной части сосуда. При
большом числе частиц вероятность![]() такой флуктуации очень мала. Рас-смотрим
зависимость этой вероятности от числа
частиц в случае, когда сосуд мысленно
разделен на две равные части.
такой флуктуации очень мала. Рас-смотрим
зависимость этой вероятности от числа
частиц в случае, когда сосуд мысленно
разделен на две равные части.
Одна
частица:
![]() .
.
Две
частицы:
![]() .
.
![]() частиц:
частиц:
![]() .
При
.
При![]() получаем
получаем![]() ,
при
,
при![]()
![]() .
В случае реального числа молекул в
газе
.
В случае реального числа молекул в
газе![]()
![]() .
Это практически нуль.
.
Это практически нуль.
В
этом, в частности, заключается причина
необратимости процесса расширения газа
в вакуум, рассмотренного в лекции 10.
Молекулы никогда снова не соберутся в
той части сосуда, где они находились до
открытия перегородки. Это относится к
возврату в начальное состояние во всех
необратимых процессах.![]()
Флуктуации
испытывают и все другие физические
величины, описывающие в целом состояние
термодинамической системы. Можно
показать, что относительная флуктуация
любой величины, зависящей от числа
![]() молекул в данном объеме с ростом
молекул в данном объеме с ростом![]() убывает как
убывает как![]() .
Например, относительная флуктуация
давления газа при
.
Например, относительная флуктуация
давления газа при![]() составляет
составляет![]() .
При давлениях порядка
.
При давлениях порядка![]() атм
(высокий вакуум) она уже равна
атм
(высокий вакуум) она уже равна![]() .
Но это все равно очень малая величина.
.
Но это все равно очень малая величина.
Итак, состояние равновесия замкнутой термодинамической системы имеет максимальную вероятность и максимальную энтропию. Обе эти величины возрастают при приближении к состоянию равновесия. На этом основана следующая гипотеза.
Гипотеза Больцмана.
Между
энтропией системы
![]() в
каждом состоянии и вероятностью этого
состояния
в
каждом состоянии и вероятностью этого
состояния![]() существует однозначная связь
существует однозначная связь![]() .
.
Больцман установил конкретный вид этой связи.
Формула Больцмана.
![]() .
.
Здесь
![]() - постоянная Больцмана, введенная в
лекции 2 при описании свойств идеального
газа. Формула Больцмана отражает другую
сторону понятия энтропии, а именно ее
статис-тический, или вероятностный
смысл. Это позволяет трактоватьэнтропию
как меру беспо-рядка в системе.
Например, начальное состояние в процессе
расширения газа в вакуум является
упорядоченным – все молекулы собраны
в одной части объема. Конечное состо-яние
равновесия является полным беспорядком
в силу хаотичности теплового движения
молекул. Таким образом, чем выше беспорядок
в системе, тем больше ее энтропия.
- постоянная Больцмана, введенная в
лекции 2 при описании свойств идеального
газа. Формула Больцмана отражает другую
сторону понятия энтропии, а именно ее
статис-тический, или вероятностный
смысл. Это позволяет трактоватьэнтропию
как меру беспо-рядка в системе.
Например, начальное состояние в процессе
расширения газа в вакуум является
упорядоченным – все молекулы собраны
в одной части объема. Конечное состо-яние
равновесия является полным беспорядком
в силу хаотичности теплового движения
молекул. Таким образом, чем выше беспорядок
в системе, тем больше ее энтропия.
Второй закон термодинамики является универсальным законом природы. Неоднократно предлагались некоторые мысленные процессы, которые на первый взгляд приводят к нарушению этого закона. При этом замкнутая система без внешнего вмешательства может переходить от большего беспорядка к меньшему, то есть самопроизвольно уменьшается ее энтропия. Но при подробном рассмотрении всегда оказывается, что предлагаемые примеры не могут быть реализованы на практике. Приведем один из таких мысленных процессов.
Демон Максвелла.
Р

Лекция 12. Термодинамические функции. Эффект Джоуля – Томсона.
Мы
уже ввели три однозначные функции
состояния термодинамической системы:
внутрен-нюю энергию
![]() ,
энтальпию
,
энтальпию
![]() и энтропию
и энтропию
![]() .
Введем еще две важнейшие термодинами-ческие
функции.
.
Введем еще две важнейшие термодинами-ческие
функции.
Свободная
энергия:
![]() .
.
Первый закон термодинамики можно представить в виде:
![]() .
.
Отсюда получаем, что
![]() .
При
.
При
![]()
![]() .
.
Из
этого соотношения видно, в чем состоит
физический смысл этой функции. Убыль
свободной энергии в квазистатическом
изотермическом процессе равна работе,
произве-денной системой. Величину
![]() называютсвязанной
энергией.
Ее нельзя перевести в работу.
называютсвязанной
энергией.
Ее нельзя перевести в работу.
Термодинамический
потенциал:
![]() ,
,
![]() .
.
Если
термодинамическая система находится
во внешней среде с постоянным давлением
![]() и постоянной температурой
и постоянной температурой![]() ,
то убыль термодинамического потенциала
в квазистати-ческом процессе равнаполезной
работе,
совершаемой системой. Под полезной
работой понимается работа системы за
вычетом работы против сил внешнего
давления.
,
то убыль термодинамического потенциала
в квазистати-ческом процессе равнаполезной
работе,
совершаемой системой. Под полезной
работой понимается работа системы за
вычетом работы против сил внешнего
давления.
Таким образом, приходим к следующей системе уравнений:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Такие
зависимости функций
![]() от термодинамических параметров
называютсяканоническими
уравнениями состояния вещества.
Они были введены Гиббсом. Из формулы
математического анализа для дифференциала
функции двух переменных отсюда легко
получить следующие соотношения:
от термодинамических параметров
называютсяканоническими
уравнениями состояния вещества.
Они были введены Гиббсом. Из формулы
математического анализа для дифференциала
функции двух переменных отсюда легко
получить следующие соотношения:
![]() ,
,
![]() ,
(1)
,
(1)
![]() ,
,
![]() , (2)
, (2)
![]() ,
,
![]() ,
(3)
,
(3)
![]() ,
,
![]() .
(4)
.
(4)
С
помощью этих уравнений можно получить
важные соотношения для расчета различных
термодинамических процессов. Можно
представить функции
![]() и
и![]() в виде
в виде
![]() ,
,
![]() .
.
Подставляя
соотношения (3) и (4) для
![]() в правые части этих уравнений, приходим
курав-нениям
Гиббса – Гельмгольца
в правые части этих уравнений, приходим
курав-нениям
Гиббса – Гельмгольца
![]() ,
,
![]() .
.
Проводя повторное дифференцирование в уравнениях (1) – (4) и используя теорему о пере-мене порядка дифференцирования, получаем соотношения Максвелла
![]() ,
(5)
,
(5)
![]() ,
(6)
,
(6)
![]() ,
(7)
,
(7)
![]() ,
(8)
,
(8)
Соотношения
Максвелла также часто используются при
выводе различных термодинами-ческих
соотношений. Такой метод называется
методом
термодинамических потенциалов.
Получим еще одно важное уравнение.
Поделив выражение для
![]() на
на![]() , находим
, находим
![]() .
.
С помощью уравнения (8) преобразуем это соотношение к виду
![]() .
(9)
.
(9)
Это уравнение понадобится нам при расчете эффекта Джоуля – Томсона.
Эффект Джоуля – Томсона.
В

![]() ,
,![]() и температуры
и температуры![]() ,
,![]() .
Пусть в начальном состоянии газ занимал
объем
.
Пусть в начальном состоянии газ занимал
объем![]() в левой части цилиндра, а в конечном
состоянии – объем
в левой части цилиндра, а в конечном
состоянии – объем![]() в правой части. Тогда полная работа газа
в этом процессе
в правой части. Тогда полная работа газа
в этом процессе![]() .
Из первого закона термодинамики с учетом
условия теплоизоляции получаем, что
.
Из первого закона термодинамики с учетом
условия теплоизоляции получаем, что![]() .
Подставляя выражение для
.
Подставляя выражение для![]() ,
приходим к сохранению энтальпии
,
приходим к сохранению энтальпии![]() .
.
Опыты
Джоуля и Томсона показали, что в случае
идеального газа температура газа не
изменяется. Для реального газа
![]() .
Изменение температуры газа в таком
процессе называетсяэффектом
Джоуля – Томсона.
Рассмотрим так называемый дифференциальный
эффект Джоуля -–Томсона,
когда
.
Изменение температуры газа в таком
процессе называетсяэффектом
Джоуля – Томсона.
Рассмотрим так называемый дифференциальный
эффект Джоуля -–Томсона,
когда
![]() .
Пусть при этом наблюдается неко-торая
малая разность температур
.
Пусть при этом наблюдается неко-торая
малая разность температур![]() .
Тогда из условия сохранения энтальпии
получим
.
Тогда из условия сохранения энтальпии
получим
![]() .
(10)
.
(10)
Из
определения энтальпии следует, что
![]() .
Тогда с помощью (9) и (10) получим
.
Тогда с помощью (9) и (10) получим
 .
(11)
.
(11)
Зная уравнение состояния газа, из уравнения (11) можно определить изменение температуры в эффекте Джоуля – Томсона. Для одного моля идеального газа
![]() ,
,
![]() .
Отсюда из (11) получаем, что для идеального
газа
.
Отсюда из (11) получаем, что для идеального
газа![]() .
.
Для
реального газа необходимо знать его
уравнение состояния. В дальнейшем мы
проведем анализ значения
![]() и в этом случае.
и в этом случае.
Лекция 13. Статистическое описание систем одинаковых частиц. Распределения Ферми – Дирака и Бозе – Эйнштейна.
Вещество в любом агрегатном состоянии представляет собой систему из большого числа частиц. Существует два вида описания таких систем.
Динамическое описание.
Частицы
пронумерованы с номерами от 1 до
![]() .
Мгновенное состояние системы опреде-ляется
заданием их координат
.
Мгновенное состояние системы опреде-ляется
заданием их координат![]() и скоростей
и скоростей![]() .
Это обычный подход, используемый в
механике.
.
Это обычный подход, используемый в
механике.
Статистическое описание.
Пространство координат и скоростей (фазовое пространство) разбивается на ячейки и рас-сматриваются вероятности состояний с разным числом частиц в ячейках. При этом, если мы считаем частицы различимыми, то задание числа частиц в каждой ячейке с указанием их номеров, называется микросостоянием системы. Если частицы неразличимы, то задаются только числа частиц в каждой ячейке – макросостояние системы.
Пусть
![]() - вероятность попадания молекулы в
- вероятность попадания молекулы в![]() - ую ячейку с объемом
- ую ячейку с объемом![]() .
Если полный объем системы равен
.
Если полный объем системы равен![]() , то
, то![]() . Перемещение частицы внутри ячейки не
меняет микросостояния. Следовательно,вероятность
микросостояния
равна
. Перемещение частицы внутри ячейки не
меняет микросостояния. Следовательно,вероятность
микросостояния
равна
![]() .
.
Найдем
теперь вероятность макросостояния.
Пусть задано макросостояние
![]() .
Возьмем какое-либо микросостояние с
теми же числами частиц в ячейках.
Представим себе, что все частицы
закреплены на своих местах. Проведем
все возможные перестановки
.
Возьмем какое-либо микросостояние с
теми же числами частиц в ячейках.
Представим себе, что все частицы
закреплены на своих местах. Проведем
все возможные перестановки![]() частиц. При этом число частиц в каждой
ячейке не изменится. Общее число
перестановок равно
частиц. При этом число частиц в каждой
ячейке не изменится. Общее число
перестановок равно![]() .
Но здесь учтены и все перестановки
внутри одной ячейки, не приводящие к
новым микросостояниям. Число таких
перестановок внутри
.
Но здесь учтены и все перестановки
внутри одной ячейки, не приводящие к
новым микросостояниям. Число таких
перестановок внутри![]() - ой ячейки равно
- ой ячейки равно![]() .
Тогда полное число микросостояний для
данного макросостояния
.
Тогда полное число микросостояний для
данного макросостояния
![]() .
.
Вероятность макросостояния
![]()

![]() .
.
Для
одинаковых ячеек объемом
![]() вероятность
вероятность![]() .
Тогда
.
Тогда![]() .
.
До
сих пор под
![]() понималась математическая вероятность
с условием
понималась математическая вероятность
с условием![]() .
В статисти-ческой физике более удобной
является нормировка, когда вероятность
задается целыми числами. Множитель
.
В статисти-ческой физике более удобной
является нормировка, когда вероятность
задается целыми числами. Множитель![]() не
зависит от чисел
не
зависит от чисел![]() .
Поэтому в такой норми-ровке можно
записать
.
Поэтому в такой норми-ровке можно
записать
![]() .
.
Статистический
вес макросостояния
![]() - число равновероятных состояний, каждое
из которых реализует данное макросостояние.
- число равновероятных состояний, каждое
из которых реализует данное макросостояние.
В модели Максвелла – Больцмана частицы считаются различимыми и при подсчете числа микросостояний считается, что если две частицы поменялись ячейками, то это различные микросостояния. Соответствующая этой модели статистическая теория называется статисти-кой Максвелла – Больцмана.
В
квантовой теории частицы считаются
неразличимыми. При этом оказывается,
что статис-тическое описание определяется
спином частиц. Спин
– квантовая величина, связанная с
собственным моментом импульса частицы.
Спин называется полуцелым,
если его проекция на выделенное
направление равна нечетному числу
![]() , где
, где![]() ,
,![]() -
постоянная Планка. Если такая проекция
выражается целым числом значений
-
постоянная Планка. Если такая проекция
выражается целым числом значений![]() ,
то такой спин называетсяцелым.
К частицам с полуцелым спином, относятся,
в частности. электроны, протоны и
нейтроны, а к частицам с целым спином –
фотоны,
,
то такой спин называетсяцелым.
К частицам с полуцелым спином, относятся,
в частности. электроны, протоны и
нейтроны, а к частицам с целым спином –
фотоны,
![]() и
и![]() мезоны
и т.д.
мезоны
и т.д.
Модель Ферми – Дирака.
Для системы взаимодействующих частиц с полуцелым спином (фермионы) в каждом заданном состоя-нии может находиться не более одной частицы (принцип Паули).
Модель Бозе – Эйнштейна.
Для системы частиц с целым спином (бозоны) в каждом заданном состоянии может находиться сколько угодно частиц.
Распределение Ферми – Дирака.
Пусть
![]() - число частиц на квантовом уровне с
энергией
- число частиц на квантовом уровне с
энергией![]() ,
а
,
а![]() - число состояний на этом уровне. В
статистической доказывается, что для
фермионов имеет место распределение
Ферми – Дирака
- число состояний на этом уровне. В
статистической доказывается, что для
фермионов имеет место распределение
Ферми – Дирака
 ,
где
,
где
![]() - нормировочная константа (химический
потенциал).
- нормировочная константа (химический
потенциал).
Распределение Бозе – Эйнштейна для бозонов отличается от этого выражения лишь знаком “ - ” перед единицей в знаменателе.
Оба
эти распределения переходят в распределение
Максвелла – Больцмана при
![]() .
.
Лекция 14. Химический потенциал. Третье начало термодинамики.
В
распределениях Ферми – Дирака и Бозе
– Эйнштейна из условия нормировки
![]() возникает параметр
возникает параметр![]() ,
который называетсяхимическим
потенциалом.
Рассмотрим термо-динамическое определение
этой величины. Она вводится для описания
тепловых процессов с переменным числом
частиц, что, например, имеет место в
химических реакциях. При
,
который называетсяхимическим
потенциалом.
Рассмотрим термо-динамическое определение
этой величины. Она вводится для описания
тепловых процессов с переменным числом
частиц, что, например, имеет место в
химических реакциях. При
![]() первый закон термодинамики можно
представить в виде
первый закон термодинамики можно
представить в виде
![]() .
.
Если
![]() изменяется, то в этом уравнении нужно
добавить слагаемое, пропорциональное
изменению числа частиц
изменяется, то в этом уравнении нужно
добавить слагаемое, пропорциональное
изменению числа частиц![]()
![]() .
.
Коэффициент
![]() называетсяхимическим
потенциалом.
называетсяхимическим
потенциалом.
Аналогичные выражения можно записать и для остальных термодинамических функций (лекция 12)
![]() ,
,
![]() ,
,
![]() .
.
Из этих соотношений вытекают следующие формулы для химического потенциала
![]() =
=
![]() =
=![]() =
=![]() .
.
Отдельно
остановимся на связи между химическим
и термодинамическим потенциалами. В
силу аддитивности
![]() можно записать
можно записать
![]() ,
где
,
где
![]() - произвольная константа.
- произвольная константа.
Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]()
![]() =
=![]() ,
или
,
или![]() .
.
Таким образом, химический потенциал равен термодинамическому потенциалу, отнесен-ному к одной частице.
Можно
показать, что параметр
![]() в распределениях Ферми – Дирака и Бозе
– Эйнштейна удовлетворяет этому
определению.
в распределениях Ферми – Дирака и Бозе
– Эйнштейна удовлетворяет этому
определению.
Третье начало термодинамики (теорема Нернста).
При приближении к абсолютному нулю энтропия термодинамической системы стремится к определенному конечному пределу. Все процессы при абсолютном нуле температур, перево-дящие систему из одного равновесного состояния в другое равновесное состояние, происхо-дят без изменения энтропии.
Изменение
энтропии при переходе из состояния с
температурой
![]() в состояние с темпера-турой
в состояние с темпера-турой![]() можно представить в виде
можно представить в виде
 .
.
Первая
часть теоремы Нернста говорит о том,
что этот интеграл сходится при
![]() .
Во второй части утверждается, что
предельное значение интеграла не зависит
от того, в каком состоянии окажется
система.
.
Во второй части утверждается, что
предельное значение интеграла не зависит
от того, в каком состоянии окажется
система.
В
связи с тем, что энтропия определена с
точностью до произвольной константы,
можно ввести понятие абсолютной
энтропии:
![]() при
при![]() .
Тогда теорему Нернста можно сформулировать
в другом виде.
.
Тогда теорему Нернста можно сформулировать
в другом виде.
При приближении к абсолютному нулю абсолютная энтропия системы стремится к нулю, независимо от параметров, характеризующих ее состояние.
Абсолютный
нуль недостижим, поэтому о справедливости
теоремы Нернста можно судить по поведению
вещества вблизи
![]() .
Практическую важность имеют следствия
из теоремы Нернста.
.
Практическую важность имеют следствия
из теоремы Нернста.
Следствие 1.
При
температуре, стремящейся к абсолютному
нулю, теплоемкости
![]() и
и![]() вещества также стремятся к нулю.
вещества также стремятся к нулю.
Отсюда, в частности, следует очень важный вывод о том, что теплоемкость вещества должна зависеть от температуры.
Следствие 2.
При приближении температуры к абсолютному нулю, внутренняя энергия вещества переста-ет зависеть от температуры.
Лекция 15. Силы взаимодействия между молекулами. Уравнение Ван-дер-Ваальса.
Для
одного моля идеального газа
![]() .
Эксперименты показывают, что при сжатии
одного моля реального газа
.
Эксперименты показывают, что при сжатии
одного моля реального газа![]() ,
то есть реальные газы менее сжимаемы.
Имеется также ряд других отличий свойств
реального газа, о которых мы будем
говорить далее. Эти отличия обусловлены
взаимодействием молекул друг с другом.
Силы взаимодействия между молекулами
имеют электромагнитную и квантовую
природу. На малых расстояниях они
проявляются как силы отталкивания, что
вызывает малую сжимаемость плотных
газов и жидкостей, сопротивление твердых
тел сжатию т.д. На больших расстояниях
они ведут себя как силы притяжения. Это
приводит к возникновению сил поверхностного
натяжения в жид-костях, к сопротивлению
растяжения твердых тел.
,
то есть реальные газы менее сжимаемы.
Имеется также ряд других отличий свойств
реального газа, о которых мы будем
говорить далее. Эти отличия обусловлены
взаимодействием молекул друг с другом.
Силы взаимодействия между молекулами
имеют электромагнитную и квантовую
природу. На малых расстояниях они
проявляются как силы отталкивания, что
вызывает малую сжимаемость плотных
газов и жидкостей, сопротивление твердых
тел сжатию т.д. На больших расстояниях
они ведут себя как силы притяжения. Это
приводит к возникновению сил поверхностного
натяжения в жид-костях, к сопротивлению
растяжения твердых тел.
Н

![]() имеет место положение равновесия, в
котором
имеет место положение равновесия, в
котором![]() .
Ниже изображена аналогичная зависимость
для энергии взаимодействия двух молекул
.
Ниже изображена аналогичная зависимость
для энергии взаимодействия двух молекул![]() .
При
.
При![]() эта энергия принимает минимальное
значение
эта энергия принимает минимальное
значение![]() .
Оно определяет вид агрегатного состояния
вещества:
.
Оно определяет вид агрегатного состояния
вещества:
![]() -
газообразное состояние,
-
газообразное состояние,
![]() -
жидкое состояние,
-
жидкое состояние,
![]() -
твердое состояние.
-
твердое состояние.
Уравнение состояния с учетом межмолекулярного взаимодействия.
Для одного моля идеального газа
![]() .
.
В
простейшей модели можно учесть влияние
сил отталкивания с помощью введения в
правую часть этого константы
![]() ,
зависящей от размера молекул
,
зависящей от размера молекул
![]() .
.
Силы
притяжения между молекулами приводят
к уменьшению давления, так как при
подлете молекулы к стенке сосуда соседние
молекулы тормозят ее движение. В грубом
приближении такое уменьшение
пропорционально концентрации молекул
![]() .
Само давление также пропорционально
концентрации, поэтому общее уменьшение
давления будет пропорционально
.
Само давление также пропорционально
концентрации, поэтому общее уменьшение
давления будет пропорционально![]() ,
или
,
или![]() .
Таким образом, получаем
.
Таким образом, получаем
![]() ,
или
,
или
![]() ,
(1)
,
(1)
где
![]() -
некоторая константа, связанная с силами
притяжения. Уравнение (1) называетсяуравнением
Ван-дер-Ваальса
для одного моля реального газа. Параметры
-
некоторая константа, связанная с силами
притяжения. Уравнение (1) называетсяуравнением
Ван-дер-Ваальса
для одного моля реального газа. Параметры
![]() и
и![]() назы-ваютсяконстантами
Ван-дер-Ваальса.
Уравнение (1) легко обобщается на случай
про-извольной массы газа
назы-ваютсяконстантами
Ван-дер-Ваальса.
Уравнение (1) легко обобщается на случай
про-извольной массы газа
![]() :
:
![]() .
.
Изотермы Ван-дер-Ваальса.
Н

![]() .
При этом
.
При этом![]() .
Эти кривые суще-ственно отличаются от
изотерм идеального газа.
.
Эти кривые суще-ственно отличаются от
изотерм идеального газа.
При
![]() они имеют волнообразный участок. При
они имеют волнообразный участок. При![]() (критическая
температура)
изотерма имеет точку перегиба
(критическая
температура)
изотерма имеет точку перегиба
![]() (критическая
точка).
Величины
(критическая
точка).
Величины
![]() ,
,![]() ,
,![]() ,
соответствующие этой точки называютсякритическими
параметрами вещества.
Их физический смысл мы обсудим далее.
Критические параметры можно выразить
через константы Ван-дер-Ваальса
,
соответствующие этой точки называютсякритическими
параметрами вещества.
Их физический смысл мы обсудим далее.
Критические параметры можно выразить
через константы Ван-дер-Ваальса
![]() и
и![]() .
.
В
точке перегиба функции
![]() ,
как известно из матанализа,
,
как известно из матанализа,![]() .
Кроме этого в точке
.
Кроме этого в точке![]() выполняется условие
выполняется условие![]() ,
так как в ней сливаются две точки
экстремума. Применяя эти соотношения
к уравнению (1), можно получить:
,
так как в ней сливаются две точки
экстремума. Применяя эти соотношения
к уравнению (1), можно получить:
![]() ,
,
![]() ,
,![]() .
.
Лекция 16. Фазовые переходы. Адиабатическое расширение реального газа.
Экспериментальные изотермы реального газа.
В опытах Эндрюса (1886 г.) по изотермическому сжатию углекислого газа были получены экспериментальные изотермы, изображенные на рис. 1.

На
экспериментальных кривых при
![]() имеется горизонтальный участок
имеется горизонтальный участок![]() на котором
на котором![]() ,
,![]() .
При
.
При![]() точки
точки![]() и
и![]() сливаются и переходят в критическую
точку
сливаются и переходят в критическую
точку![]() .
.
В
экспериментах было обнаружено, на
участке
![]() вещество находится в
жидком состоянии,
на участке
вещество находится в
жидком состоянии,
на участке
![]() -одновременно
в жидком и газообразном состоянии,
на участке
-одновременно
в жидком и газообразном состоянии,
на участке
![]() -в
газо-образном состоянии.
Таким образом, в процессе изотермического
сжатия реального газа имеет место
фазовый
переход
из газа в жидкость.
-в
газо-образном состоянии.
Таким образом, в процессе изотермического
сжатия реального газа имеет место
фазовый
переход
из газа в жидкость.
Н

![]() при разных температурах
при разных температурах
![]() .
Газообразное состояние при
.
Газообразное состояние при
![]() называетсяпаром.
Он конденсируется в жидкость при
изотермическом сжатии. Пар, находящийся
в динамическом равновесии с жидкостью
над ее поверхностью при данной температуре,
называется насыщенным
паром. Кривая
называетсяпаром.
Он конденсируется в жидкость при
изотермическом сжатии. Пар, находящийся
в динамическом равновесии с жидкостью
над ее поверхностью при данной температуре,
называется насыщенным
паром. Кривая
![]() представляет собой границу между жидким
состоянием и областью фазового перехода
«жидкость – пар». Ее называюткривой
кипения. Кривая
конденсации
представляет собой границу между жидким
состоянием и областью фазового перехода
«жидкость – пар». Ее называюткривой
кипения. Кривая
конденсации
![]() отделяет
двухфазную область от газообразного
состояния. При
отделяет
двухфазную область от газообразного
состояния. При![]() исчезает область двухфазного состояния.
При
исчезает область двухфазного состояния.
При![]() газ нельзя перевести в жидкое состояние
путем изотермического сжатия.
газ нельзя перевести в жидкое состояние
путем изотермического сжатия.
Особое поведение вещества имеет место вблизи критической точки - критическое состояние вещества. В этой области нет различия между жидким и газообразным состояниями. По-верхность жидкости отсутствует и нет поверхностного натяжения. Обе фазы существуют одновременно, не переходя одна в другую.
Внутренняя энергия реального газа.
По общему определению внутренней энергии (лекция 3) она равна
![]() .
.
Кинетическую
энергию молекул
![]() можно по-прежнему считать равной
можно по-прежнему считать равной![]() (1 моль). Для вычисления потенциальной
энергии взаимодействия
(1 моль). Для вычисления потенциальной
энергии взаимодействия![]() нужно вычислить работу сил «внутреннего
давления»
нужно вычислить работу сил «внутреннего
давления»![]() ,
связанных с силами притяжения:
,
связанных с силами притяжения:
 ,
то есть
,
то есть
![]() .
.
Таким образом, внутренняя энергия 1 моля реального газа
![]() .
.
С помощью этого выражения рассмотрим процессы адиабатического расширения реального газа.
1. Равновесное адиабатическое расширение.
Для идеального газа из первого начала термодинамики
![]() ,
,
![]() .
.
Для реального газа
![]() ,
,
 .
.
Таким образом при равновесном адиабатическом расширении охлаждение реального газа выше, чем идеального. Это происходит из-за того, что в реальном газе часть внутренней энергии расходуется на преодоление сил притяжения между молекулами.
2. Расширение газа в вакуум.
В
таком процессе мы считаем, что
![]() ,
,![]() (лекция 10),
(лекция 10),![]() .
Тогда для идеального газа
.
Тогда для идеального газа![]() .
.
Для реального газа
![]() ,
,
![]() ,
так как
,
так как
![]() .
.
Реальный газ при расширении в вакуум охлаждается. В этом процессе часть кинетической энергии теплового движения молекул переходит в потенциальную энергию их взаимодей-ствия.
3. Процесс Джоуля-Томсона.
В лекции 4 было показано, что в этом процессе сохраняется энтальпия
![]() .
.
Для
идеального газа отсюда следует, что
![]() .
.
Для реального газа
![]() .
.
В
этом случае уже нельзя считать, что
![]() и температура будет изменяться в
зависи-мости от параметров. Для нахождения
изменения температуры воспользуемся
формулой (11) из лекции 12 в случае
дифференциального эффекта Джоуля –
Томсона
и температура будет изменяться в
зависи-мости от параметров. Для нахождения
изменения температуры воспользуемся
формулой (11) из лекции 12 в случае
дифференциального эффекта Джоуля –
Томсона
 .
.
С помощью уравнения Ван-дер-Ваальса можно преобразовать это выражение к следующему виду
![]() .
.
Разделив
числитель и знаменатель в правой части
этого уравнения на
![]() и принимая во внимание, что
и принимая во внимание, что![]() и
и![]() ,
приходим к приближенному выражению
,
приходим к приближенному выражению
![]() .
.
Параметр
![]() называетсякоэффициентом
Джоуля – Томсона,
а величина
называетсякоэффициентом
Джоуля – Томсона,
а величина
![]() -температурой
инверсии.
При
-температурой
инверсии.
При
![]() (
(![]() )
газ охлаждается, а при
)
газ охлаждается, а при![]() - нагревается. Температуру инверсии
можно выразить через критическую
температуру
- нагревается. Температуру инверсии
можно выразить через критическую
температуру![]() :
:
![]() .
.
Например,
для кислорода
![]() температура инверсии
температура инверсии![]() .
Эффект Джоуля – Томсона используется
для сжижения газов.
.
Эффект Джоуля – Томсона используется
для сжижения газов.
Лекция 17. Сжижение газов. Жидкий гелий.
В установках для сжижения газов обычно сначала производится адиабатическое охлаждение газа до температуры ниже температуры инверсии, а затем многократно производится про-цесс Джоуля – Томсона. Вместо пористой перегородки используется отверстие определен-ного диаметра (дроссель). Сам процесс продува газа через отверстие называется дроссели-рованием. Устройство, в котором газ предварительно охлаждается адиабатически, называет-ся детандером.
Н

Сжиженные газы позволяют получать низкие темпера-туры в интервалах от температур их кипения при атмосферном давлении до температур отвердевания, которые достигаются путем откачивания паров над ними. Исключение составляет жидкий гелий, не твердеющий ни при каком охлаждении. Приведем значения этих интервалов температур для некоторых газов: 63,1 – 77,30К - жидкий азот, 54,4 – 90,10К – жидкий кислород, 0,7 – 4,20К – жидкий гелий.
При
кипении жидкого гелия под пониженным
давлением путем откачивания паров над
ним можно достичь температур порядка
0,70К.
Дальнейшее понижение температуры гелия
таким способом невозможно, так как
насосы не успевают откачивать пары до
столь низких темпе-ратур. Эти температуры
называют сверхнизкими.
Для дальнейшего охлаждения в области
сверхнизких температур используют
магнитный
метод охлаждения.
Он основан на исполь-зовании парамагнитных
солей с магнитной проницаемостью
![]() .
Намагниченный обра-зец размагничивают
адиабатическим образом путем удаления
из магнитного поля, что приводит к его
дальнейшему охлаждению. Этот процесс
можно объяснить на основе второго закона
термодинамики. Полная энтропия образца
из парамагнитной соли
.
Намагниченный обра-зец размагничивают
адиабатическим образом путем удаления
из магнитного поля, что приводит к его
дальнейшему охлаждению. Этот процесс
можно объяснить на основе второго закона
термодинамики. Полная энтропия образца
из парамагнитной соли
![]() .
.
При
размагничивании возникает беспорядок
в ориентации магнитных моментов молекул.
Поэтому слагаемое
![]() возрастает, а в силу сохранения
возрастает, а в силу сохранения![]() (адиабатичность)
(адиабатичность)![]() уменьшается. Это означает охлаждение
образца.
уменьшается. Это означает охлаждение
образца.
Жидкий гелий.
Можно
сказать, что жидкий гелий является самой
холодной жидкостью в природе. Его
критическая температура
![]() .
Остальные сжиженные газы ведут себя
подобно обычным жидкостями. При понижении
температуры у них возрастают вязкость
и силы поверхностного натяжения.
Поведение жидкого гелия кардинально
отличается от свойств других сжиженных
газов.
.
Остальные сжиженные газы ведут себя
подобно обычным жидкостями. При понижении
температуры у них возрастают вязкость
и силы поверхностного натяжения.
Поведение жидкого гелия кардинально
отличается от свойств других сжиженных
газов.
Две модификации жидкого гелия.

На
рис. 2 представлена экспериментальная
кривая зависимости теплоемкости жидкого
гелия от тем-пературы. Теплоемкость
изменяется скачком вблизи температуры
![]() ,
которая называется
,
которая называется![]() -
точкой
(кривая
-
точкой
(кривая
![]() подобна
букве
подобна
букве![]() ).
Как мы увидим далее, скачок теплоем-кости
является характерным свойством фазовых
переходов второго рода. Свойства жидкого
гелия слева и справа от
).
Как мы увидим далее, скачок теплоем-кости
является характерным свойством фазовых
переходов второго рода. Свойства жидкого
гелия слева и справа от![]() различаются кардинальным образом.
ЖидкийHe
I
(
различаются кардинальным образом.
ЖидкийHe
I
(![]() )
обладает обыч-ными для сжиженного газа
свойствами. У жидкого He
II
(
)
обладает обыч-ными для сжиженного газа
свойствами. У жидкого He
II
(![]() )
практически отсутствует вязкость, то
есть он обладает свойством
сверхтекучести.
При этом течение He
II
происходит по весьма странным по
сравнению с обычными жидкостями законам.
Его скорость течения не зависит от
разности давлений на концах капилляра.
С увеличением радиуса капилляра скорость
уменьшается. По формуле Пуазейля она
должна увеличиваться ~
)
практически отсутствует вязкость, то
есть он обладает свойством
сверхтекучести.
При этом течение He
II
происходит по весьма странным по
сравнению с обычными жидкостями законам.
Его скорость течения не зависит от
разности давлений на концах капилляра.
С увеличением радиуса капилляра скорость
уменьшается. По формуле Пуазейля она
должна увеличиваться ~![]() .
Все эти экзотические свойства, как было
показано Л.Д. Ландау (1941 г.), обусловлены
квантовыми эффектами.
.
Все эти экзотические свойства, как было
показано Л.Д. Ландау (1941 г.), обусловлены
квантовыми эффектами.
Теория Ландау.
При
![]() жидкий
гелий находится в состоянии, когда
энергия и импульс его атомов не могут
изменяться. Можно сказать, такая что
жидкость являетсяневозбужденной.
Частицы не могут обмениваться импульсами,
что означает отсутствие вязкости. При
жидкий
гелий находится в состоянии, когда
энергия и импульс его атомов не могут
изменяться. Можно сказать, такая что
жидкость являетсяневозбужденной.
Частицы не могут обмениваться импульсами,
что означает отсутствие вязкости. При
![]() ,
но
,
но![]() возбуждается
только часть жидкости и возникает смесь
возбужденной и невозбуж-денной компонент
(вязкой и безвязкостной). Эта смесь и
представляет собой модификацию He
II.
Тогда можно понять причину странного
поведения течения He
II
через капилляры. Чем уже капилляр, тем
меньше влияние вязкой компоненты и
свойства потока определяются квантовыми
закономерностями. При увеличении радиуса
капилляра влияние вязкой компо-ненты
возрастает и скорость течения падает.
В теории Ландау He
II
рассматривается как квантовая
жидкость,
в которой энергия выделяется и поглощается
звуковыми квантами – фононами.
возбуждается
только часть жидкости и возникает смесь
возбужденной и невозбуж-денной компонент
(вязкой и безвязкостной). Эта смесь и
представляет собой модификацию He
II.
Тогда можно понять причину странного
поведения течения He
II
через капилляры. Чем уже капилляр, тем
меньше влияние вязкой компоненты и
свойства потока определяются квантовыми
закономерностями. При увеличении радиуса
капилляра влияние вязкой компо-ненты
возрастает и скорость течения падает.
В теории Ландау He
II
рассматривается как квантовая
жидкость,
в которой энергия выделяется и поглощается
звуковыми квантами – фононами.
Опыты Капицы.
П

![]() - точку не только резко уменьшается
вязкость жидкого гелия, но и на много
порядков возрастает его теплопроводность.
При этом теплопроводность в основном
происходит с помощью особого механизма
конвекции. Суть его состоит в том, что
нагреваниеHe
II
приводит к его обеднению сверхтекучей
компонентой и образуется разность ее
концентраций. Так как ее вязкость рана
нулю, то начинается движение жидкости,
выравнивающее концентрацию. Такой
механизм был продемонстрирован в опытах
П.Л. Капицы (1941 г.). Схема одного из этих
опытов представлена на рис. 3. Малый
стеклянный сосуд с впаянными нагревате-лем
и термометром и открытой трубкой в конце
помещал-ся в сосуд с жидким гелием. При
пропускании тока через нагреватель
наблюдался поворот крылышка на нити.
Он был вызван действием возбужденной
компоненты. Но при этом уровень гелия
в малом сосуде не изменялся, так внутрь
него входила невозбужденная компонента
He
II.
- точку не только резко уменьшается
вязкость жидкого гелия, но и на много
порядков возрастает его теплопроводность.
При этом теплопроводность в основном
происходит с помощью особого механизма
конвекции. Суть его состоит в том, что
нагреваниеHe
II
приводит к его обеднению сверхтекучей
компонентой и образуется разность ее
концентраций. Так как ее вязкость рана
нулю, то начинается движение жидкости,
выравнивающее концентрацию. Такой
механизм был продемонстрирован в опытах
П.Л. Капицы (1941 г.). Схема одного из этих
опытов представлена на рис. 3. Малый
стеклянный сосуд с впаянными нагревате-лем
и термометром и открытой трубкой в конце
помещал-ся в сосуд с жидким гелием. При
пропускании тока через нагреватель
наблюдался поворот крылышка на нити.
Он был вызван действием возбужденной
компоненты. Но при этом уровень гелия
в малом сосуде не изменялся, так внутрь
него входила невозбужденная компонента
He
II.
Лекция 18. Объемные свойства жидкостей. Явления переноса в жидкостях. Поверхностное натяжение.
Сжимаемость жидкостей.
Для
описания этого свойства вводится понятие
коэффициента
сжимаемости
(при
![]() )
)
![]() .
.
Конкретная
зависимость
![]() от
от![]() и
и![]() определяется
уравнением состояния вещества. Для
жидкостей из опытных данных следует
зависимость
определяется
уравнением состояния вещества. Для
жидкостей из опытных данных следует
зависимость
![]() ,
где
,
где
![]() ,
,![]() .
.
Жидкости
по сравнению с газами малосжимаемы.
Значение
![]() для них изменяется в интервале от 10-5
до 10-4
атм-1.
для них изменяется в интервале от 10-5
до 10-4
атм-1.
Тепловое расширение жидкостей.
Описывается
с помощью коэффициента
объемного расширения
(при
![]() )
)
![]() .
.
С
помощью уравнения состояния
![]() можно получить связь между коэффициен-тами
можно получить связь между коэффициен-тами![]() и
и![]() .
При
.
При![]()
![]() .
Отсюда
.
Отсюда
![]() .
.
Величина
![]() для жидкостей может достигать очень
больших значений. В частности, по этой
причине нельзя перегревать ртутный
термометр, так как при заполнении ртутью
всего объема капилляра небольшое
увеличение температуры приведет к его
разрушению.
для жидкостей может достигать очень
больших значений. В частности, по этой
причине нельзя перегревать ртутный
термометр, так как при заполнении ртутью
всего объема капилляра небольшое
увеличение температуры приведет к его
разрушению.
Явления переноса в жидкостях.
Процессы
переноса в жидкостях отличаются от
соответствующих процессов в газах. Это
обусловлено особым характером движения
молекул в жидкостях. Основную часть
времени молекулы совершают колебания
около положений равновесия. Когда
энергия молекул ста-новится больше
некоторого предельного значения, они
могут совершить скачок на рассто-яние
![]() в новое положение равновесия. Такой
механизм лежит в основемодели
Френкеля
для описания процессов переноса в
жидкостях. В ней вводится понятие
среднего времени «оседлой» жизни
молекулы
в новое положение равновесия. Такой
механизм лежит в основемодели
Френкеля
для описания процессов переноса в
жидкостях. В ней вводится понятие
среднего времени «оседлой» жизни
молекулы
![]() ,
в течение которого она совершает
колебания. Тогда сред-нюю скорость
перемещения молекулы по всему объему
жидкости можно определить как
,
в течение которого она совершает
колебания. Тогда сред-нюю скорость
перемещения молекулы по всему объему
жидкости можно определить как![]() ,
где средняя длина скачка. Рассмотрим с
помощью такой модели процесс диффузии.
Для идеального газа в лекции 7 было
получено выражение для коэффициента
диффузии
,
где средняя длина скачка. Рассмотрим с
помощью такой модели процесс диффузии.
Для идеального газа в лекции 7 было
получено выражение для коэффициента
диффузии
![]() .
Для жидкости его можно представить в
виде
.
Для жидкости его можно представить в
виде
![]() .
.
Множитель
![]() появляется из-за того, что движение
молекул носит характер случайных
блужданий и вдоль каждого направления
движется в среднем
появляется из-за того, что движение
молекул носит характер случайных
блужданий и вдоль каждого направления
движется в среднем![]() молекул. Вероятность получить энергию
молекул. Вероятность получить энергию![]() ,
необходимую для скачка (энергия
активации)
можно найти с помощью распределения
Больцмана
,
необходимую для скачка (энергия
активации)
можно найти с помощью распределения
Больцмана
![]() .
.
Можно считать, что время оседлой жизни обратно пропорционально этой вероятности, то есть
![]() .
.
До
скачка молекула совершала колебания с
частотой
![]() ,
поэтому
,
поэтому![]() и окончательно получим
и окончательно получим
![]() .
.
Из этого выражения следует, что диффузия в жидкостях происходит намного медленнее, чем в газах.
Для
описания внутреннего
трения в жидкостях
можно исходить из того, что вязкость
тем меньше, чем меньше среднее время
оседлой жизни, то есть
![]() .
Отсюда
.
Отсюда
![]() .
.
Следовательно,
вязкость жидкости уменьшается при
нагревании. При этом коэффициент
![]() слабо зависит от температуры.
слабо зависит от температуры.
Поверхностное натяжение жидкостей.
Н

![]() может быть представлена в виде
может быть представлена в виде
![]() (
(![]() при
при![]() ),
или
),
или![]() .
.
Величина
![]() называетсякоэффициентом
поверхностного натяжения;
[
называетсякоэффициентом
поверхностного натяжения;
[![]() ]
= 1 Дж/м2
= 1 Н/м = 103
дин/см. Так как поверхностный слой
жидкости обладает избыточной потенциальной
энергией
]
= 1 Дж/м2
= 1 Н/м = 103
дин/см. Так как поверхностный слой
жидкости обладает избыточной потенциальной
энергией
![]() ,
то можно дать другое определение
,
то можно дать другое определение![]()
![]() ,
,
![]() ,
или
,
или![]()
В
изотермическом процессе
![]() ,
где
,
где![]() -
свободная энергия. Поэтому
-
свободная энергия. Поэтому
![]() ,
,
![]() .
.
В
равновесии потенциальная энергия
![]() и свободная энергия
и свободная энергия![]() имеют минимальное значение. Вместе с
ними площадь поверхности жидкости
имеют минимальное значение. Вместе с
ними площадь поверхности жидкости![]() также
должна принимать мини-мальное значение
также
должна принимать мини-мальное значение![]() .
Следовательно, должны возникать силы,
стремящиеся сократить поверхность
жидкости. Эти силы всегда направлены
по касательной к поверхности и назы-ваютсясилами
поверхностного натяжения.
.
Следовательно, должны возникать силы,
стремящиеся сократить поверхность
жидкости. Эти силы всегда направлены
по касательной к поверхности и назы-ваютсясилами
поверхностного натяжения.

Рассмотрим простой опыт, в котором наглядно проявляется действие сил поверхностного натяжения. Пусть на проволоч-ной рамке с одной подвижной стороной находится мыльная пленка (рис. 2). Пленка имеет две поверхности, поэтому условие равновесия имеет вид
![]() ,
,
![]() .
.
Работа
сил поверхностного натяжения при
перемещении перекладины на расстояние
![]()
![]() .
.
Отсюда
![]() .
С помощью этого выражения можно вычислить
коэффициент поверхност-ного натяжения
исследуемой жидкости. Из этих выражений
вытекает также еще одно опре-деление
еще одно определение коэффициента
поверхностного натяжения
.
С помощью этого выражения можно вычислить
коэффициент поверхност-ного натяжения
исследуемой жидкости. Из этих выражений
вытекает также еще одно опре-деление
еще одно определение коэффициента
поверхностного натяжения
![]() ,
,
где
![]() -
длина прямолинейного участка границы
поверхности, а
-
длина прямолинейного участка границы
поверхности, а
![]() -
сила поверхностного натяжения, действующая
на этот участок.
-
сила поверхностного натяжения, действующая
на этот участок.
Лекция 19. Равновесие жидкости на границе двух сред. Капиллярные явления.
Рассмотрим силы поверхностного натяжения, действующие на границе соприкосновения жидкости с другими средами.
Граница двух жидкостей.
П

![]() действуют следующие силы поверхностного
натяжения:
действуют следующие силы поверхностного
натяжения:![]() -
сила на границе между жидкостями 1 и 2;
-
сила на границе между жидкостями 1 и 2;![]() - сила на границе между жидкостью 1 и
газом;
- сила на границе между жидкостью 1 и
газом;![]() - сила на границе между жидкостью 2 и
газом. При этом
- сила на границе между жидкостью 2 и
газом. При этом![]() ,
,![]() .
Условия равновесия капли имеют вид:
.
Условия равновесия капли имеют вид:
![]() ,
,
![]() .
.
Углы
![]() и
и![]() называютсякраевыми
углами.
Подставляя выражения для сил, получаем
называютсякраевыми
углами.
Подставляя выражения для сил, получаем
![]() ,
,
![]() .
.
Возводя обе части этих уравнений в квадрат и складывая их, приходим к следующему условию равновесия
![]() ,
где
,
где
![]() .
.
При
![]() капля жидкости 2 приобретает форму
чечевицы, а при
капля жидкости 2 приобретает форму
чечевицы, а при![]() она растекается тонкой пленкой по
поверхности жидкости 1.
она растекается тонкой пленкой по
поверхности жидкости 1.
Граница жидкости и твердого тела.
Р

![]() ,
или
,
или
![]() .
.
При
условии
![]() угол
угол![]() ,
то есть жидкость растекается по
поверхности твердого тела в виде тонкой
пленки. Такое явление носит названиеполного
смачивания.
При
,
то есть жидкость растекается по
поверхности твердого тела в виде тонкой
пленки. Такое явление носит названиеполного
смачивания.
При
![]() имеет месточастичное
смачива-ние,
при
имеет месточастичное
смачива-ние,
при
![]() -частичное
несмачивание,
а при
-частичное
несмачивание,
а при
![]() -полное
несмачивание.
-полное
несмачивание.
Дополнительное давление за счет кривизны поверхности жидкости.
Равнодействующая сил поверхностного натяжения направлена к центру кривизны поверх-ности жидкости. Это приводит к возникновению дополнительного давления, зависящего от кривизны поверхности.
Сферическая поверхность жидкости.
При
изменении радиуса поверхности на
величину
![]() силы дополнительного давления совершают
работу
силы дополнительного давления совершают
работу![]() .
С другой стороны эта работа равна
.
С другой стороны эта работа равна![]() .
Отсюда получаемформулу
Лапласа для сферической поверхности
жидкости
.
Отсюда получаемформулу
Лапласа для сферической поверхности
жидкости
![]() .
.
Цилиндрическая поверхность жидкости.
Рассмотрим
цилиндрическую поверхность жидкости
радиуса
![]() и высоты
и высоты![]() .
Тогда, рассуждая аналогично, имеем
.
Тогда, рассуждая аналогично, имеем![]() .
Отсюда следуетформула
Лапласа для цилиндрической поверхности
.
Отсюда следуетформула
Лапласа для цилиндрической поверхности
![]() .
.
Произвольная поверхность жидкости.
![]() .
.
Здесь
![]() ,
,![]() - главные радиусы кривизны поверхности
(максимальный и минимальный).
- главные радиусы кривизны поверхности
(максимальный и минимальный).
Капиллярные явления.
Поверхностное натяжение жидкости может приводить к значительным силам, действующим как на саму жидкость, так и на тела с которыми она соприкасается. Это проявляется в так называемых капиллярных явлениях, возникающих, когда размеры поверхности сравнимы с ее радиусом кривизны.
Капиллярный подъем жидкости.
Р

![]() , где
, где![]() -
радиус капилляра,
-
радиус капилляра,![]() - краевой угол. Тогда из условия равновесия
жидкости
- краевой угол. Тогда из условия равновесия
жидкости
![]() получаем
получаем
![]() .
.
Если жидкость не смачивает стенки капилляра, то эта формула будет определять расстояние от поверхности жидкости в сосуде, на которое опус-тится уровень в капилляре.
Лекция 20. Испарение и кипение. Свойства растворов.
Наиболее быстрые молекулы могут покинуть жидкость, образуя пар над ее поверхностью. Переход молекул из жидкости в пар называется испарением. Если не подводить к жидкости дополнительное тепло, то она при испарении охлаждается. Процесс обратного перехода молекул в жидкость называется конденсацией. Жидкость может находиться в динамическом равновесии со своим паром, когда среднее число молекул, покидающих жидкость в единицу времени равно среднему числу возвращающихся молекул. При этом пар называется насы-щенным. Такое равновесие устанавливается, если жидкость находится в закрытом сосуде. Если испарение жидкости происходит при постоянной температуре, к ней необходимо подводить тепло.
Скрытая
теплота испарения
![]() - количество тепла, которое нужно подвести
для того, чтобы испарить определенное
количество жидкости без изменения ее
температуры при внешнем давлении, равном
давлению ее насыщенных паров.
- количество тепла, которое нужно подвести
для того, чтобы испарить определенное
количество жидкости без изменения ее
температуры при внешнем давлении, равном
давлению ее насыщенных паров.
При
изотермической конденсации пара в
жидкость аналогичная теплота будет
выделяться. Скрытая теплота испарения
уменьшается с ростом температуры,
обращаясь в нуль при
![]() .
.
Зависимость давления насыщенного пара от температуры.
С помощью распределения Больцмана можно записать выражение для концентрации молекул пара
![]() ,
,
где
![]() -
концентрация молекул жидкости,
-
концентрация молекул жидкости,![]() - молярная скрытая теплота испарения.
Пар можно считатьидеальным
газом,
для которого справедливо уравнение
Клапейрона
- молярная скрытая теплота испарения.
Пар можно считатьидеальным
газом,
для которого справедливо уравнение
Клапейрона
![]() .
.
Из этого выражения видно, что давление (упругость) насыщенного пара возрастает с ростом температуры. Его удобно записать в виде
![]() .
(1)
.
(1)
На
этой формуле основан один из методов
измерения величины
![]() .
.
Влияние кривизны поверхности жидкости на давление насыщенного пара.
Пусть
жидкость находится в закрытом сосуде
и в нее частично погружена капиллярная
трубка, полностью смачиваемая жидкостью.
Так как сосуд закрыт, то над поверхностью
жидкости находится насыщенный пар.
Жидкость поднимется в капилляре на
высоту
![]() (лекция 19). С другой стороны давление
пара на высоте
(лекция 19). С другой стороны давление
пара на высоте![]() ,
где
,
где![]() давление пара над плоской поверхностью.
Из этих двух выражений получаем
давление пара над плоской поверхностью.
Из этих двух выражений получаем
![]() .
.
При
![]() получаем формулу длядавления
насыщенного пара над вогнутой поверхностью
жидкости
получаем формулу длядавления
насыщенного пара над вогнутой поверхностью
жидкости
![]() ,
где
,
где
![]() - плотность пара,
- плотность пара,![]() - плотность жидкости.
- плотность жидкости.
Аналогичным образом можно получить такое соотношение для случая выпуклой поверх-ности жидкости
![]() .
.
Из последней формулы, в частности, следует, что рост дождевых капель возможен только в том случае, если парциальное давление паров воды в воздухе больше не только упругости насыщенного пара при той же температуре, но и упругости паров над поверхностью капли малого радиуса. В обычных условиях минимальный начальный размер капель обеспечивае-тся за счет мельчайших пылинок (аэрозолей), содержащихся в воздухе. Они играют роль зародышей в процессе конденсации паров.
Кипение жидкостей.
Кипением называется процесс испарения жидкости, сопровождающийся быстрым образо-ванием пузырьков пара, прорывающихся через поверхность жидкости наружу.
Роль зародышей в процессе кипения выполняют мельчайшие пузырьки воздуха (или другого газа), содержащиеся в жидкости. Для кипения жидкости необходимо довести ее температуру до значения, при котором упругость ее насыщенных паров равна внешнему давлению. Так как давление насыщенного пара зависит от температуры, то отсюда следует, что температура кипения зависит от внешнего давления. Из формулы (1) легко получить
 ,
или
,
или
![]() (
(![]() - молярный объем пара).
- молярный объем пара).
Значит температура насыщенного пара возрастает с ростом его упругости. Следовательно, и температура кипения должна возрастать с ростом внешнего давления.
М

![]() ,
учитывающую объемы начальной и конечной
фазы. Для вывода этой формулы рассмотрим
следующий бесконечно малый цикл Карно
(рис. 1), в котором рабочим телом
является жидкость, переходящая в пар.
Пусть в точке
,
учитывающую объемы начальной и конечной
фазы. Для вывода этой формулы рассмотрим
следующий бесконечно малый цикл Карно
(рис. 1), в котором рабочим телом
является жидкость, переходящая в пар.
Пусть в точке![]() 1 моль жидкости занимает весь объем
сосуда с подвижным поршнем равный
1 моль жидкости занимает весь объем
сосуда с подвижным поршнем равный![]() .
На участке
.
На участке![]() производится изотермическое испарение
жидкос-ти. В точке
производится изотермическое испарение
жидкос-ти. В точке![]() вся жидкость переходит в пар с молярным
объемом
вся жидкость переходит в пар с молярным
объемом![]() .
На участке
.
На участке![]() происходит адиабатическое расширение
пара. При этом давление уменьшается на
величину
происходит адиабатическое расширение
пара. При этом давление уменьшается на
величину![]() ,
а температура – на
,
а температура – на![]() .
На участке
.
На участке![]() пар изотермически сжимается до полной
конденсации в жидкость. На этапе
пар изотермически сжимается до полной
конденсации в жидкость. На этапе![]() производится адиабатическое сжатие
жидкости до начального давления
производится адиабатическое сжатие
жидкости до начального давления![]() и начальной температуры
и начальной температуры![]() .
Работа за цикл, совершаемая рабочим
телом
.
Работа за цикл, совершаемая рабочим
телом![]() .
Тогда по теореме Карно для к.п.д. цикла
получим
.
Тогда по теореме Карно для к.п.д. цикла
получим
![]() .
.
Таким образом, мы приходим к уравнению Клапейрона – Клаузиуса
![]() .
.
Оно
описывает зависимость давления от
температуры для фазового
перехода первого рода
c
молярным объемом начальной фазы
![]() и молярным объемом конечной фазы
и молярным объемом конечной фазы![]() .
Стро-гое определение понятия фазового
перехода первого рода будет дано в
дальнейшем. Здесь пока отметим, что к
этому типу относятся такие хорошо
известные перехода как испарение,
конденсация, плавление, отвердевание
и т. д. В этот же класс входят переходы
из одного кристаллического состояния
вещества в другое, например переход
графит – алмаз.
.
Стро-гое определение понятия фазового
перехода первого рода будет дано в
дальнейшем. Здесь пока отметим, что к
этому типу относятся такие хорошо
известные перехода как испарение,
конденсация, плавление, отвердевание
и т. д. В этот же класс входят переходы
из одного кристаллического состояния
вещества в другое, например переход
графит – алмаз.
Свойства растворов.
Раствором
называется жидкая смесь двух веществ,
в которой одно из веществ содержится в
количестве большем, чем другое
(растворитель).Если
![]() ,
,![]() - число молей каждого ве-щества в растворе,
то содержание каждого из них удобно
описывать с помощьюмолярных
концентраций
- число молей каждого ве-щества в растворе,
то содержание каждого из них удобно
описывать с помощьюмолярных
концентраций
![]() ,
,
![]() .
.
Раствор с максимальной концентрацией растворенного вещества называется насыщенным раствором.
Теплота растворения равна работе против сил притяжения растворенного вещества. Раство-ры, для которых теплота растворения равна нулю, называются идеальными. Растворы малой концентрации можно считать идеальными. Для идеальных растворов справедлив закон Рауля
![]() ,
,
![]() .
.
Здесь
![]() - растворитель,
- растворитель,![]() - растворенное вещество,
- растворенное вещество,![]() -
давление паров над раствором,
-
давление паров над раствором,![]() -
давление насыщенных паров над чистыми
веществами. С помощью закона Рауля и
уравнения Клапейрона – Клаузиуса можно
получить формулу дляпонижения
температуры кипения раствора
-
давление насыщенных паров над чистыми
веществами. С помощью закона Рауля и
уравнения Клапейрона – Клаузиуса можно
получить формулу дляпонижения
температуры кипения раствора
![]() .
.
Лекция 21. Свойства твердых тел и кристаллические решетки.
Твердые тела делятся на два вида – кристаллические и аморфные. В кристаллических твер-дых телах атомы расположены в строгом порядке с определенным видом симметрии во всем объеме (дальний порядок). В аморфных телах упорядочены лишь соседние атомы (ближний порядок). Аморфные тела, например, стекло, можно рассматривать как жидкости, обладаю-щие очень большой вязкостью при обычных температурах. При нагревании таких тел их вязкость уменьшается и они ведут себя как жидкости.

У кристаллических твердых тел переход в жидкое состояние происходит скачком при температуре плавления (рис. 1). Температура аморфных тел при нагревании монотонно возрастает. Далее под твердыми телами мы будем подразумевать только кристаллические твердые тела.
При
охлаждении расплавленных твердых тел
происходит образование кристаллической
решетки. При этом атомы располагаются
в кристаллической решетке таким образом,
чтобы их энергия взаимодействия принимала
минимальное значение
![]() (лекция 15). Расстоя-ние между атомами
(лекция 15). Расстоя-ние между атомами![]() является в этом случаеположением
равновесия.
В кристаллической решетке атомы вдоль
различных направлений располагаются
с различной плотностью. Если провести
через узлы решетки всевозможные плоскости
(атомные
плоскости),
то плотность их заселения атомами будет
различной. Этим объясняется различие
свойств кристаллов в разных направлениях
– анизотропия.
Плотно заселенные атомные плоскости
отстоят дальше друг друга, чем менее
заселенные и поэтому они легко отделяются
друг от друга (плоскости
спайности).
По этой причине графит и слюда раскалываются
на тонкие пластинки, каменная соль на
параллелепипеды и т.д.
является в этом случаеположением
равновесия.
В кристаллической решетке атомы вдоль
различных направлений располагаются
с различной плотностью. Если провести
через узлы решетки всевозможные плоскости
(атомные
плоскости),
то плотность их заселения атомами будет
различной. Этим объясняется различие
свойств кристаллов в разных направлениях
– анизотропия.
Плотно заселенные атомные плоскости
отстоят дальше друг друга, чем менее
заселенные и поэтому они легко отделяются
друг от друга (плоскости
спайности).
По этой причине графит и слюда раскалываются
на тонкие пластинки, каменная соль на
параллелепипеды и т.д.
Периодическое
расположение атомов в решетке можно
осуществить с помощью операции
параллельного перемещения – трансляции.
Трансляцию можно задать в виде трех
векторов
![]() в разных направлениях. Тогда пространственная
решетка может в виде
в разных направлениях. Тогда пространственная
решетка может в виде
![]() ,
где
,
где
![]() - целые числа.
- целые числа.
Параллелепипед,
построенный на векторах
![]() ,
называетсяэлементарной
ячейкой.
Эти векторы имеют порядок межатомных
расстояний
в кристаллах (
,
называетсяэлементарной
ячейкой.
Эти векторы имеют порядок межатомных
расстояний
в кристаллах (![]() см).
см).
Элементы симметрии в кристалле.
1. Ось симметрии.
В
этом случае кристалл может быть совмещен
сам с собой путем поворота на некоторый
угол вокруг этой оси. При этом угол
поворота
![]() ,
,![]() .
.
2. Плоскость симметрии.
Одна половина кристалла совмещается с другой при зеркальном отражении ее в плоскости симметрии.
3. Центр симметрии.
Если
в кристалле существует точка, обладающая
тем свойством, что при замене радиуса
– вектора
![]() любого из узлов, проведенного из такой
точки, на
любого из узлов, проведенного из такой
точки, на![]() ,
кристалл переходит в состояние,
неотличимое от исходного. Такая точка
называетсяцентром
симметрии.
,
кристалл переходит в состояние,
неотличимое от исходного. Такая точка
называетсяцентром
симметрии.
4. Поворотно – зеркальная ось.
Кристалл обладает поворотно – зеркальной осью симметрии, если его можно совместить с самим собой, повернув на некоторый угол вокруг оси и отразив в плоскости, перпендику-лярной к этой оси.
Кристаллы могут обладать несколькими элементами симметрии. Всего существует 32 возможные комбинации элементов симметрии. Они называются классами симметрии. В кристаллографии эти 32 класса объединяют в 7 систем симметрии в порядке возрастания симметрии: 1) триклинная система (2 класса); 2) моноклинная система (3); 3) ромбическая система (3); 4) тригональная система (7); 5) гексагональная система (5); 6) тетрагональная система (7); 7) кубическая система (5).
Все перечисленные элементы симметрии описывают симметрию кристалла в целом – макро- симметрия. Существует также микросимметрия, связанная с тем, что любую решетку можно представить в виде правильно уложенных элементарных ячеек. При этом симметрия обус-ловлена возможностью получения всего кристалла путем трансляции. Элементарная ячейка представляет собой параллелепипед, построенный путем параллельного переноса какого либо из узлов по трем направлениям. Она называется решеткой Браве. В ней атомы могут располагаться не только в вершинах, но также в центре граней (гранецентрированная решет-ка Браве) и в центре диагональной плоскости (объемноцентрированная решетка Браве). Всего существует 14 различных типов решеток Браве. Каждая из может быть отнесена к одной из 7 – ми систем симметрии. На рис. 2 приведены структуры некоторых решеток Браве.

Лекция 22. Связь упругих свойств со структурой кристаллической решетки. Дефекты в кристаллах.
П
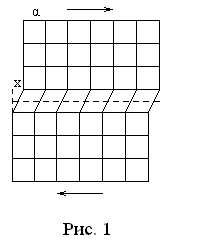
![]() ,
,![]() и
и![]() .
Таким образом, напряжение сдвига
.
Таким образом, напряжение сдвига![]() является периодической функцией
является периодической функцией![]() и его можно аппроксимировать выражением
и его можно аппроксимировать выражением
![]() .
.
Здесь
![]() является критическим скалывающим
напряжением, необходимым для скольже-ния
атомных плоскостей. По величине оно
близко к пределу упругости. При
является критическим скалывающим
напряжением, необходимым для скольже-ния
атомных плоскостей. По величине оно
близко к пределу упругости. При![]()
![]() ,
где
,
где
![]() - угол сдвига.
- угол сдвига.
Отсюда
с помощью закона Гука для деформации
сдвига
![]() получаем
получаем
![]() .
.
О

![]() кристалл считался идеальным, то есть
имеющим строго периодическую структуру.
На самом деле, в реальных кристаллах
всегда имеютсядефекты,
то есть нарушения периодич-ности. Главное
влияние на упругие свойства твердых
тел оказывают дефекты, называемые
дислокациями.
Рассмотрим простейший тип таких дефектов
– краевую дислокацию.
В этом случае в одной части кристалла
возникает на одну атом-ную плоскость
больше, чем в другой (рис. 2). Наруше-ние
периодичности при этом имеет место в
области
кристалл считался идеальным, то есть
имеющим строго периодическую структуру.
На самом деле, в реальных кристаллах
всегда имеютсядефекты,
то есть нарушения периодич-ности. Главное
влияние на упругие свойства твердых
тел оказывают дефекты, называемые
дислокациями.
Рассмотрим простейший тип таких дефектов
– краевую дислокацию.
В этом случае в одной части кристалла
возникает на одну атом-ную плоскость
больше, чем в другой (рис. 2). Наруше-ние
периодичности при этом имеет место в
области
![]() вдоль линии на краю лишней плоскости.
Атомы, распо-ложенные вдоль этой линии
лишены нормального окружения соседними
атомами. Дислокации возникают в процессе
роста кристалла, а также под влиянием
внеш-них воздействий. Они могут
перемещаться в плоскости скольжения.
Поэтому под действием внешнего
напря-жения энергетически более выгодно
переместить дислокацию вместо перемещения
атомной плоскости. Можно привести
аналогию со складкой на ковре: склад-ку
легче устранить ее перемещением, чем с
помощью приложения силы к краю ковра.
вдоль линии на краю лишней плоскости.
Атомы, распо-ложенные вдоль этой линии
лишены нормального окружения соседними
атомами. Дислокации возникают в процессе
роста кристалла, а также под влиянием
внеш-них воздействий. Они могут
перемещаться в плоскости скольжения.
Поэтому под действием внешнего
напря-жения энергетически более выгодно
переместить дислокацию вместо перемещения
атомной плоскости. Можно привести
аналогию со складкой на ковре: склад-ку
легче устранить ее перемещением, чем с
помощью приложения силы к краю ковра.
Наличием
дислокаций в реальном кристалле и
объясняется малое значение предела
пластич-ности по сравнению с
![]() ,
о котором шла речь выше. Это подтверждается
в опытах с монокристаллами, выращенными
в условиях, исключающих появление
дислокаций. В этом случае предельное
напряжение близко к теоретическому.
Если в кристалле имеется большое
количество дислокаций, то их подвижность
уменьшается и кристалл становится более
проч-ным. Это проявляется при повторных
пластических деформациях (ковка,
или наклеп)
метал-лических изделий, повышающих их
прочность. Существует много других
видов дефектов, влияющих на свойства
твердых тел.
,
о котором шла речь выше. Это подтверждается
в опытах с монокристаллами, выращенными
в условиях, исключающих появление
дислокаций. В этом случае предельное
напряжение близко к теоретическому.
Если в кристалле имеется большое
количество дислокаций, то их подвижность
уменьшается и кристалл становится более
проч-ным. Это проявляется при повторных
пластических деформациях (ковка,
или наклеп)
метал-лических изделий, повышающих их
прочность. Существует много других
видов дефектов, влияющих на свойства
твердых тел.
Примесные дефекты.
В этом случае в кристаллической решетке присутствует небольшое количество посторонних атомов. Атомы примесей скапливаются в области дислокаций, что уменьшает их подвиж-ность и приводит к повышению прочности твердых тел. Например, добавляя примесь угле-рода в мягкое чистое железо мы получаем прочный металл сталь. При отжиге подвижность дислокаций увеличивается из-за того, что атомы примесей в результате диффузии покидают свои места и распределяются равномерно по всему объему.
Вакансии (дефекты Шоттки).
При таком дефекте некоторые узлы решетки оказываются незанятыми. Это вызывает сме-щение соседних атомов по сравнению с их нормальным положением. Как будет показано далее, вакансии играют важную роль в процессе диффузии в твердом теле.
Дефекты Френкеля (вакансия плюс дополнительный узел).
Такой дефект возникает, если какой-нибудь атом покидает свое место в узле решетки и помещается где-то между другими узлами. В этом случае возникает сразу два нарушения периодичности в расположении атомов (пара Френкеля).
Зависимость деформации твердых тел от напряжения.
Д

![]() и относительная деформация
и относительная деформация![]() пропорциональны друг другу. Максимальное
напряжение
пропорциональны друг другу. Максимальное
напряжение![]() ,
при котором деформация еще остается
упругой, называетсяпределом
упругости. На рис. 3
представлена экспериментальная
зависимость
,
при котором деформация еще остается
упругой, называетсяпределом
упругости. На рис. 3
представлена экспериментальная
зависимость
![]() от
от![]() .
Если повысить
.
Если повысить![]() до
до![]() то деформация определяется отрезком
то деформация определяется отрезком![]() .
При постепенном уменьшении напряжения
до нуля деформация уменьшается до
.
При постепенном уменьшении напряжения
до нуля деформация уменьшается до![]() ,
что соответствует остаточной, илипластической деформации.
Если после этого тело снова подвергнуть
действию напряжения, то предел упругости
оказывается близок к максимальному
значению
,
что соответствует остаточной, илипластической деформации.
Если после этого тело снова подвергнуть
действию напряжения, то предел упругости
оказывается близок к максимальному
значению
![]() при начальном воздействии. Это явление
своеобразной «памяти» кристалла связано
с ростом числа дислокаций при пластической
деформации (наклеп).
при начальном воздействии. Это явление
своеобразной «памяти» кристалла связано
с ростом числа дислокаций при пластической
деформации (наклеп).
Лекция 23. Переход в твердое состояние. Диаграммы состояния и фазовые переходы.
Вещество
может перейти в твердое состояние
(кристаллизация)
как из жидкого состояния, так и из
газообразного. При этом выделяется
скрытая теплота кристаллизации![]() .
Обратный переход из твердого состояния
в газообразное называетсясублимацией.
Все эти переходы являются фазовыми
переходами 1 – го рода. Зависимость
температуры перехода от давления
описывается уравнением Клапейрона –
Клаузиуса
.
Обратный переход из твердого состояния
в газообразное называетсясублимацией.
Все эти переходы являются фазовыми
переходами 1 – го рода. Зависимость
температуры перехода от давления
описывается уравнением Клапейрона –
Клаузиуса
![]() .
.
Для
большинства веществ молярный объем
жидкой фазы больше молярного объема
твердой фазы, то есть
![]() . Поэтому для них температура кристаллизации
растет с ростом дав-ления. Исключение
составляют вода, висмут, сурьма и
германий, для которых
. Поэтому для них температура кристаллизации
растет с ростом дав-ления. Исключение
составляют вода, висмут, сурьма и
германий, для которых![]() и соответственно температура перехода
с ростом давления падает.
и соответственно температура перехода
с ростом давления падает.
В случае перехода из твердого состояния в газообразное для разрушения кристаллической решетки телу необходимо передать скрытую теплоту сублимации
![]() ,
,
так как можно перевести твердое тело сначала в жидкость, а затем – в пар.
К

![]() ,
,![]() (рис. 1). Эти кривые формируютдиаграмму
состояния вещества. Точка,
в которой они соединяются, называется
тройной точкой.
В окрестности этой точки три фазы
вещества находятся в равновесии. Кривая
сублимации начинается в
нуле и заканчи-вается в тройной точке.
Кривая парообразования
имеет начало имеет начало в тройной
точке, а конец – в критической точке
(рис. 1). Эти кривые формируютдиаграмму
состояния вещества. Точка,
в которой они соединяются, называется
тройной точкой.
В окрестности этой точки три фазы
вещества находятся в равновесии. Кривая
сублимации начинается в
нуле и заканчи-вается в тройной точке.
Кривая парообразования
имеет начало имеет начало в тройной
точке, а конец – в критической точке
![]() .
Кривая плавления начинается в тройной
точке и конца не имеет. Из диаграммы
состояния видно, что твердое тело не
всегда может быть переведено нагреванием
в жид-кое состояние. В случае
.
Кривая плавления начинается в тройной
точке и конца не имеет. Из диаграммы
состояния видно, что твердое тело не
всегда может быть переведено нагреванием
в жид-кое состояние. В случае![]() при нагревании оно будет испаряться.
Большинство веществ плавятся при
нагревании при атмосферном давле-нии,
так как у них
при нагревании оно будет испаряться.
Большинство веществ плавятся при
нагревании при атмосферном давле-нии,
так как у них![]() 1 атм. Однако, есть вещества, у которых
1 атм. Однако, есть вещества, у которых![]() 1 атм. Для углекис-лоты (СО2)
1 атм. Для углекис-лоты (СО2)
![]() 5,1 атм,
5,1 атм,![]() - 570 С. При
атмосферном давлении она может находиться
в равновесии со своим паром при температуре
- 800 С. Это
хорошо известный нам «сухой лед», который
никогда не плавится, а только испаряется.
- 570 С. При
атмосферном давлении она может находиться
в равновесии со своим паром при температуре
- 800 С. Это
хорошо известный нам «сухой лед», который
никогда не плавится, а только испаряется.
Полиморфные переходы.
Некоторые
вещества могут иметь несколько модификаций
одной фазы, например, несколько видов
кристаллической решетки. Переход из
одной модификации в другую называется
полиморфным
переходом.
На рис. 2 приведена диаграмма состояния
углерода в двух его модификациях –
графит и алмаз. При низких давлениях и
температурах устойчивой модифи-кацией
углерода является графит, а при
![]() атм
– алмаз. В нормальных условиях а
атм
– алмаз. В нормальных условиях а

![]() атм
и
атм
и![]() 20000
К графит может превращаться в алмаз.
Таким способом полу-чают искусственные
алмазы в промышленных условиях.
Полиморфные переходы также относятся
к фазовым переходам 1 – го рода. Рассмотрим
общие свойства этих фазовых превращений.
20000
К графит может превращаться в алмаз.
Таким способом полу-чают искусственные
алмазы в промышленных условиях.
Полиморфные переходы также относятся
к фазовым переходам 1 – го рода. Рассмотрим
общие свойства этих фазовых превращений.
Фазовые переходы первого рода.
1. Во всех переходах такого типа внутренняя энергия вещества в зависимости от темпера-туры изменяется скачкообразно (рис. 3). При этом либо выделяется, либо поглощается энергия в виде скрытой теплоты перехода.
2. Новая фаза не возникает сразу во всем объеме, а образуется в виде зародышей вокруг соответствующих центров (мелких частиц, пузырьков газа и т.д.)
Фазовые переходы второго рода.
1.
Внутренняя энергия является непрерывной
функцией температуры. Переходы не
сопро-вождаются выделением или поглощением
энергии. В точке фазового перехода
(точка
Кюри)
скачком изменяется производная
![]() то есть теплоемкость (рис. 3).
то есть теплоемкость (рис. 3).
2. Для начала перехода не требуется наличия начальных центров и переход происходит сразу во всем объеме.

Фазовым
переходом второго рода является переход
жидкого гелия из состояния
![]()
![]() в состояние
в состояние![]()
![]() ,
который мы рассмотрели в лекции 17. К
таким переходам относятся также переход
из ферромагнитного состояния в
неферромагнитное, переход некоторых
металлов из нормального состояния в
сверхпроводящее и т. д. Основную роль в
развитии фазовых переходов второго
играет рост флуктуаций физических
величин по мере прибли-жения к температуре
Кюри.
,
который мы рассмотрели в лекции 17. К
таким переходам относятся также переход
из ферромагнитного состояния в
неферромагнитное, переход некоторых
металлов из нормального состояния в
сверхпроводящее и т. д. Основную роль в
развитии фазовых переходов второго
играет рост флуктуаций физических
величин по мере прибли-жения к температуре
Кюри.
Лекция 24. Тепловые свойства твердых тел. Явления переноса в твердых телах.
Теплоемкость твердых тел.
Атомы
в твердом теле совершают колебания
около положений равновесия в узлах
решетки. Так как выполняется условие
![]() ,
то эти колебания являются малыми. Таким
образом, твердое тело можно считать
совокупностью гармонических осцилляторов.
Можно разложить колебание узла решетки
на три составляющие по осям координат.
Вдоль каждой из осей по закону равномерного
распределения энергии (лекция 2) приходится
кинетическая энергия
,
то эти колебания являются малыми. Таким
образом, твердое тело можно считать
совокупностью гармонических осцилляторов.
Можно разложить колебание узла решетки
на три составляющие по осям координат.
Вдоль каждой из осей по закону равномерного
распределения энергии (лекция 2) приходится
кинетическая энергия![]() .
Так как средняя потенциальная энергия
осциллятора равна средней кинети-ческой,
то полная энергия атома в кристалле,
приходящаяся на одну степень свободы,
равна
.
Так как средняя потенциальная энергия
осциллятора равна средней кинети-ческой,
то полная энергия атома в кристалле,
приходящаяся на одну степень свободы,
равна![]() . Тогда полная энергия атома с тремя
степенями свободы равна
. Тогда полная энергия атома с тремя
степенями свободы равна![]() .
Внутренняя энер-гия одного моля твердого
тела и его теплоемкость
.
Внутренняя энер-гия одного моля твердого
тела и его теплоемкость![]() в
этом случае равны соответственно
в
этом случае равны соответственно
![]() ,
,
![]() .
.
Последнее соотношение носит название закона Дюлонга и Пти: теплоемкость твердых тел является постоянной величиной, одинаковой для всех веществ.

Из
опыта следует, что закон Дюлонга и Пти
при обычных температурах выполняется
для боль-шинства твердых тел. Есть,
однако, вещества, не подчиняющиеся этому
закону (бор, бериллий, кремний, алмаз).
Экспериментальные данные показывают,
что при низких температурах тепло-емкость
твердых тел уменьшается, стремясь к
нулю при
![]() (рис. 1). Так и должно происходить согласно
следствию из 3 – го начала термодинамики
(лекция 14). Причина отклонения при низких
температурах от закона Дюлонга и Пти
состоит в том, что в этом случае
классический закон о равномерном
распределении энергии перестает
выполняться и движение узлов ре-шетки
нужно описывать с помощью законов
квантовой механики.
(рис. 1). Так и должно происходить согласно
следствию из 3 – го начала термодинамики
(лекция 14). Причина отклонения при низких
температурах от закона Дюлонга и Пти
состоит в том, что в этом случае
классический закон о равномерном
распределении энергии перестает
выполняться и движение узлов ре-шетки
нужно описывать с помощью законов
квантовой механики.
Теория теплоемкости твердого тела Эйнштейна.
По
законам квантовой механики энергия
частицы, совершающей колебания с частотой
![]()
![]() ,
,
где
![]() - целые числа,
- целые числа,![]() Джּсек
– постоянная Планка. Упрощающее
предпо-ложение в теории Эйнштейна:
частота колебаний
Джּсек
– постоянная Планка. Упрощающее
предпо-ложение в теории Эйнштейна:
частота колебаний
![]() одинакова для всех атомов. Распре-деление
атомов по энергиям можно описать формулой
Больцмана
одинакова для всех атомов. Распре-деление
атомов по энергиям можно описать формулой
Больцмана
![]() .
.
Тогда средняя энергия атома в узле решетки
 .
.
Проводя суммирование, приходим к выражению
 .
.
В
классическом пределе
![]()
![]() .
Тогда для одной степени свободы
.
Тогда для одной степени свободы![]() .
Для трех степеней свободы
.
Для трех степеней свободы
 ,
,
 .
(1)
.
(1)
Формула
Эйнштейна (1) дает зависимость
![]() близкую к наблюдаемой в экспериментах.
Дебаем была построена более общая
теория, учитывающая спектр частот
колебаний атомов в кристалле с максимальной
частотой
близкую к наблюдаемой в экспериментах.
Дебаем была построена более общая
теория, учитывающая спектр частот
колебаний атомов в кристалле с максимальной
частотой![]() .
Из этой теории следует, что начиная с
темпера-туры
.
Из этой теории следует, что начиная с
темпера-туры![]() (температура
Дебая),
теплоемкость начинает быстро убывать
с понижением температуры. Например, для
алмаза
(температура
Дебая),
теплоемкость начинает быстро убывать
с понижением температуры. Например, для
алмаза
![]() С
и поэтому для него закон Дюлонга и Пти
нарушается уже при комнатной температуре.
С
и поэтому для него закон Дюлонга и Пти
нарушается уже при комнатной температуре.
Тепловое расширение твердых тел.
П

Тепловое расширение характеризуется коэффициентами линейного и объемного расши-
рения
![]() ,
,
![]() .
.
При
постоянных значениях
![]() и
и![]() имеет место линейная зависимость
имеет место линейная зависимость![]() и
и![]() от
от![]() :
:
![]() ,
,
![]() .
.
Явления переноса в твердых телах.
1. Теплопроводность.
Кристаллическая
решетка представляет собой связанную
колебательную систему. Поэтому возмущения
в твердом теле передаются посредством
звуковых волн. Квантовая теория поз-воляет
сопоставить звуковым колебаниям в
твердом теле некоторые фиктивные частицы
– фононы,
энергия которых равна
![]() .
Тепловое движение в твердом теле
обусловлено фоно-нами. При абсолютном
нуле число фононов равно нулю, а с ростом
температуры оно возрас-тает ~
.
Тепловое движение в твердом теле
обусловлено фоно-нами. При абсолютном
нуле число фононов равно нулю, а с ростом
температуры оно возрас-тает ~![]() .
Твердое тело можно рассматривать как
сосуд, наполненный газом из фононеов.
Перенос тепла осуществляется путем
столкновения фононов с узлами решетки.
При этом можно считать, что выполняется
закон теплопроводности и выражение для
коэффициента
.
Твердое тело можно рассматривать как
сосуд, наполненный газом из фононеов.
Перенос тепла осуществляется путем
столкновения фононов с узлами решетки.
При этом можно считать, что выполняется
закон теплопроводности и выражение для
коэффициента![]() ,
рассмотренные в лекции 7. Тогда для
твердого тела получаем:
,
рассмотренные в лекции 7. Тогда для
твердого тела получаем:
![]() .
.
В
теории твердого тела доказывается, что
длина свободного пробега фонона
![]() ~
~![]() .
В твердом теле скорость звука не зависит
от температуры, поэтому
.
В твердом теле скорость звука не зависит
от температуры, поэтому![]() ~
~
![]() .
.
2. Диффузия.
Основную роль в диффузии в твердых телах играет переход атомов на вакантные места в кристаллической решетке. Это эквивалентно перемещению вакансий в обратном направле-нии. Для того, чтобы перемещение атомов происходило в определенном направлении, должен существовать градиент плотности вакансий. Проводя рассмотрение аналогичное случаю процесса диффузии в жидкости (лекция 18), можно представить коэффициент диффузии в твердом теле в виде
![]() ,
где
,
где
![]() -
период решетки,
-
период решетки,![]() -
среднее время пребывания атома в узле.
-
среднее время пребывания атома в узле.
Время
![]() обратно
пропорционально как вероятности
образования вакансии рядом с атомом,
так и вероятности получить энергию
обратно
пропорционально как вероятности
образования вакансии рядом с атомом,
так и вероятности получить энергию![]() ,
необходимую для перемещения в вакансию.
Тогда
,
необходимую для перемещения в вакансию.
Тогда
![]() ,
где
,
где
![]() -
энергия необходимая для образования
вакансии.
-
энергия необходимая для образования
вакансии.
