
- •Первообразная и неопределенный интеграл, их свойства.
- •Подведение под знак дифференциала
- •Метод замены переменной (метод подстановки)
- •Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
- •Примеры
- •Интегрирование по частям
- •Интегрирование рациональных дробей
- •Подведение под знак дифференциала
- •Метод замены переменной (метод подстановки)
- •Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
- •Примеры
- •Интегрирование по частям
- •Интегрирование рациональных дробей
- •ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- •Производная сложной функции.
- •Решение дифференциальных уравнений с разделяющимися переменными

13. Производная сложной функции.
Производная сложной функции.
Функции сложного вида не совсем корректно называть термином «сложная функция». К примеру,
смотрится очень внушительно, но сложной эта функция не является, в
отличие от 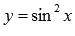 .
.
В этой статье мы разберемся с понятием сложной функции, научимся выявлять ее в составе элементарных функций, дадим формулу нахождения ее производной и подробно рассмотрим решение характерных примеров.
При решении примеров будем постоянно использовать таблицу производных и правила дифференцирования, так что держите их перед глазами.
Сложная функция – это функция, аргументом которой также является функция.
С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать какf(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).
К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую
степень, а 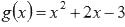 - целая рациональная функция (смотритеклассификацию элементарных функций), тогда
- целая рациональная функция (смотритеклассификацию элементарных функций), тогда 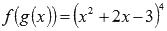 .
.
В свою очередь, g(x) также может быть сложной функцией. Например, |
. Условно |
|
такое выражение можно обозначить как |
. Здесь f – функция синуса, |
- функция |
извлечения квадратного корня, 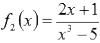 - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом
- дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом
 .
.
Часто можно слышать, что сложную функцию называют композицией функций.
Формула нахождения производной сложной функции.

14. I и II дифференциал и инвариантность.

Инвариантность Рассмотрим дифференциал сложной функции. Пусть 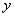 - сложная функция
- сложная функция 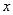 :
:
Дифференциал
этой функции, используя формулу для производной сложной функции, можно записать в виде
Но 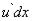 есть дифференциал функции
есть дифференциал функции 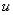 , поэтому
, поэтому
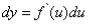 ,
,
т.е.
(13)
Здесь дифференциал записан в том же виде, как и в формуле (7), хотя аргумент 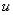 является не независимой
является не независимой
переменной, а функцией 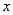 . Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливо независимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называют инвариантностью (неизменностью) формы дифференциала.
. Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливо независимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называют инвариантностью (неизменностью) формы дифференциала.
Подчеркнём, что в формуле (13) нельзя заменить 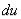 на
на 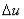 , так как
, так как
для любой функции 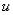 , кроме линейной.
, кроме линейной.

15. Касательная плоскость и нормаль к поверхности.
Пусть имеется поверхность, заданная уравнением 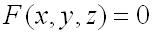 . Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку
. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку
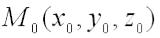 , называется касательной плоскостью к поверхности в точке
, называется касательной плоскостью к поверхности в точке  .
.
Прямая, проведенная через точку 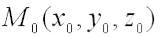 поверхности
поверхности  , перпендикулярно к касательной плоскости называется нормалью к поверхности.
, перпендикулярно к касательной плоскости называется нормалью к поверхности.
Если поверхность задана уравнением 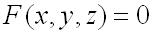 , то уравнение касательной плоскости к этой поверхности в точке
, то уравнение касательной плоскости к этой поверхности в точке  записывается в виде:
записывается в виде:
,
а уравнение нормали к поверхности в этой же точке – в виде:
.

16. Формула Тейлора.
Теорема Тейлора. 1) Пусть функция F(X) имеет в точке х = а и некоторой ее окрестности производные порядка до (N+1) включительно.{ Т. е. и все предыдущие до порядка N Функции и их производные непрерывны и дифференцируемы в этой окрестности}.
2) Пусть х - любое значение из этой окрестности, но х ¹ а.
Тогда между точками х и а найдется такая точка E, что справедлива формула:
- это выражение называется Формулой Тейлора, а выражение:
Называется Остаточным членом в форме Лагранжа.
Доказательство. Представим функцию f(x) в виде некоторого многочлена Pn(x), значение которого в точке х = а равно значению функции f(x), а значения его производных равно значениям соответствующих производных функции в точке х = а.
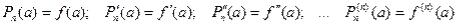 (1)
(1)
Многочлен Pn(x) будет близок к функции f(x). Чем больше значение n, тем ближе значения многочлена к значениям функции, тем точнее он повторяет функцию.
Представим этот многочлен с неопределенными пока коэффициентами:
 (2)
(2)
Для нахождения неопределенных коэффициентов вычисляем производные многочлена в точке х = а и составляем систему уравнений:
(3)
Решение этой системы при х = а не вызывает затруднений, получаем:
…………………….
Подставляя полученные значения Ci в формулу (2), получаем:
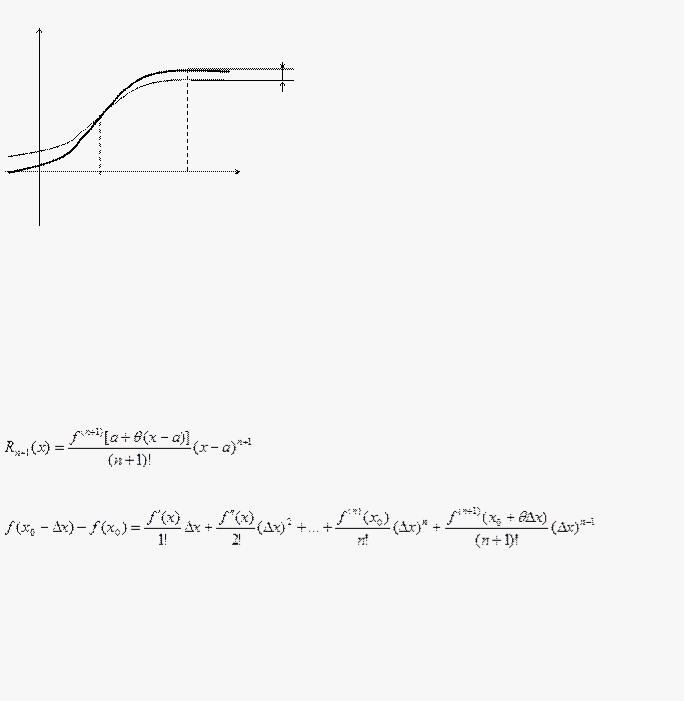
Как было замечено выше, многочлен не точно совпадает с функцией f(x), т. е. отличается от нее на некоторую величину. Обозначим эту величину Rn+1(x). Тогда:
F(x) = Pn(x) + Rn+1(x)
Теорема доказана.
Рассмотрим подробнее величину Rn+1(x). y Как видно на рисунке, в
точке х = а значение многочлена f(x)=Rn+1(x) в точности совпадает со значением функции. Pn(x) Однако, при удалении от точки х = а расхождение значений увеличивается.
Иногда используется другая запись для Rn+1(x). Т. к. точка eÎ(a, x), то найдется такое число q из интервала
0 < q < 1, что e = a + q(x – a).
Тогда можно записать:
Тогда, если принять a = x0, x – a = Dx, x = x0 + Dx, формулу Тейлора можно записать в виде:
Где 0 < q < 1
Если принять n =0, получим: F(X0 + DX) – F(X0) = F¢(X0 + QDX)×DX – это выражение
называется Формулой Лагранжа. (Жозеф Луи Лагранж (1736-1813) французский математик и механик).
Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т. д.
При рассмотрении Степенных рядов будет более подробно описаны некоторые особенности и условия разложения функции по формуле Тейлора.
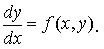
17. Дифференциальные уравнения I порядка. Общие и частные решения. Общие понятия.
F(x, y, y ') = 0,
где y = y(x) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.
Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y '(x)) ≡ 0 для всех x из (a,b) .
График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.
Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.
Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x0) = y0, называется задачей Коши (или начальной задачей).
Условие y(x0) = y0 — начальное условие.
Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.
Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.
Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называется частным интегралом уравнения.
Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:
Уравнения первого порядка часто записывают в дифференциальной форме:
M(x, y)dx + N(x, y)dy = 0.
Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y) .
