
- •Первообразная и неопределенный интеграл, их свойства.
- •Подведение под знак дифференциала
- •Метод замены переменной (метод подстановки)
- •Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
- •Примеры
- •Интегрирование по частям
- •Интегрирование рациональных дробей
- •Подведение под знак дифференциала
- •Метод замены переменной (метод подстановки)
- •Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
- •Примеры
- •Интегрирование по частям
- •Интегрирование рациональных дробей
- •ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- •Производная сложной функции.
- •Решение дифференциальных уравнений с разделяющимися переменными

Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой
Пусть требуется вычислить интеграл 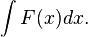 Сделаем подстановку
Сделаем подстановку  где
где 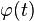
— функция, имеющая непрерывную производную.
Тогда 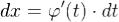 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
Интегрирование выражений вида 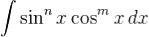
Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t. Если n и m чётные, то удобнее сделать подстановку tg x = t.
Примеры
Вычислить: 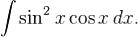 Пусть
Пусть 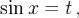 тогда
тогда 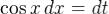 и
и
Интегрирование по частям
Основная статья: Интегрирование по частям
Интегрирование по частям — применение следующей формулы для интегрирования:
Или:
В частности, с помощью n-кратного применения этой формулы находится интеграл 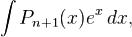 где
где 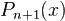 — многочлен
— многочлен 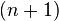 -й степени.
-й степени.
Интегрирование рациональных дробей
Основная статья: Разложение дробей при интегрировании
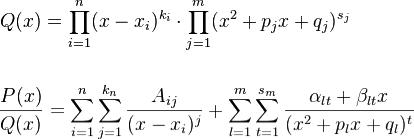
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.
Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.
Всякую правильную рациональную дробь 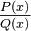 , знаменатель которой разложен на множители
, знаменатель которой разложен на множители
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
где  — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
— некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
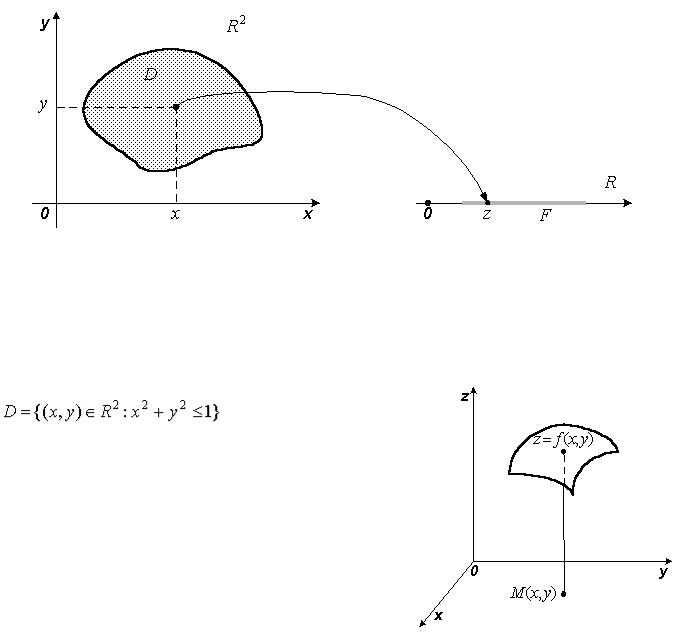
9.Предел функции многих переменных.
10.Непрерывность функции многих переменных.
ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ
1. Вводные понятия. Пусть дано множество  , и пусть указано правило, по которому каждой точке
, и пусть указано правило, по которому каждой точке  соответствует некоторое число
соответствует некоторое число  . В этом случае говорят, что задана функция
. В этом случае говорят, что задана функция
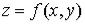 с областью определения
с областью определения 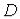 и областью значений
и областью значений  . При этом
. При этом  и
и  называют независимыми переменными (аргументами), а
называют независимыми переменными (аргументами), а 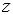 –зависимой переменной (функцией).
–зависимой переменной (функцией).
Функцию 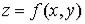 часто записывают в виде «
часто записывают в виде « ». Схематично функция может быть изображена так, как это показано на рис. 1.
». Схематично функция может быть изображена так, как это показано на рис. 1.
Рис.1.
Пример. На множестве
определим функцию
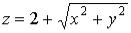 ; тогда ее областью значений является отрезок
; тогда ее областью значений является отрезок  . Эту функцию можно определить,
. Эту функцию можно определить,
конечно, и на всей плоскости 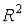 ; в этом случае имеем
; в этом случае имеем 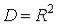 и
и 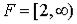 .
.
Графиком функции 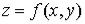 называют множество
называют множество
точек 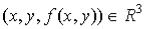 ; обычно графиком является некоторая поверхность (рис. 2).
; обычно графиком является некоторая поверхность (рис. 2).
При построении графика функции часто пользуются методом сечений.

Пример. Построить график функции |
и найти |
. |
Рис.2. |
 Воспользуемся методом сечений.
Воспользуемся методом сечений.
–в плоскости  – парабола.
– парабола.
–в плоскости 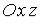 –парабола.
–парабола.
–в плоскости 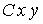 –
–
окружность.
Искомая поверхность – параболоид вращения (рис. 3). ^ |
Рис.3. |
Расстоянием между двумя произвольными точками 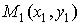 и
и 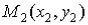 (евклидова)
(евклидова)
пространства 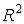 называется число
называется число
.
Множество точек 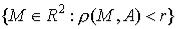 называется открытым кругом радиуса
называется открытым кругом радиуса  с центром в точке
с центром в точке
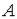 ,
, 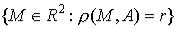 – окружностью радиуса
– окружностью радиуса 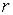 с центром в точке
с центром в точке 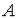 .
.
Открытый круг радиуса 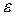 с центром в точке
с центром в точке  называется
называется 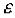 -
-
окрестностью точки 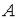 .
.
Определение. Точка 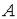 называется внутренней точкой множества
называется внутренней точкой множества 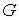 , если существует
, если существует 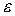 -окрестность
-окрестность 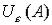 точки
точки
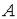 , целиком принадлежащая множеству
, целиком принадлежащая множеству  (т.е.
(т.е. 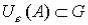 ) (рис.
) (рис.
4).
Определение. Точка |
называется граничной точкой множества |
|
, если в любой ее -окрестности содержатся точки, как принадлежащие множеству |
, так и не |
|
принадлежащие ему (рис. |
Рис.4. |
|
5). |
|
|
Граничная точка множества может как принадлежать этому множеству, так и не принадлежать ему.

Определение. Множество 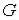 называется откры-тым, если все его точки – внутренние.
называется откры-тым, если все его точки – внутренние.
Определение. Множество 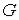 называется замк-нутым, если оно содержит все свои граничные точки. Множество всех граничных точек множества
называется замк-нутым, если оно содержит все свои граничные точки. Множество всех граничных точек множества 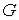 называется его границей (и часто обозначается символом
называется его границей (и часто обозначается символом 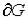 ). Заметим, что множество
). Заметим, что множество 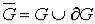 является замкнутым и называется замыканием множества
является замкнутым и называется замыканием множества
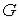 . Рис.5.
. Рис.5.
Пример. Если 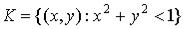 , то
, то 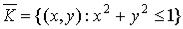 . При этом
. При этом
. Покажите это!
Определение. Точка 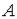 называется предельной точкой множества
называется предельной точкой множества 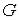 , если в любой
, если в любой 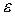 -окрестности точки
-окрестности точки 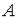 содержатся точки множества
содержатся точки множества 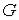 , отличные от
, отличные от 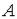 .
.
Образно говоря, точка 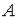 называется предельной точкой множества
называется предельной точкой множества 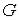 , если «к точке
, если «к точке  можно
можно
подойти сколь угодно близко, идя по точкам множества 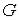 и не наступая на саму точку
и не наступая на саму точку 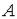 ». Предельная точка множества может принадлежать, а может не принадлежать этому множеству.
». Предельная точка множества может принадлежать, а может не принадлежать этому множеству.
Пример. Множество  совпадает с множеством своих предельных точек.
совпадает с множеством своих предельных точек.
Множество 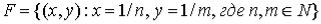 имеет единственную предельную точку
имеет единственную предельную точку
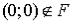 . Покажите это!
. Покажите это!
2. Предел функции.
Определение. Будем говорить, что последовательность точек 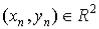 сходится при
сходится при 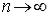 к точке
к точке  , если
, если  при
при  .
.
В этом случае точку  называют пределом указанной последовательности и пишут:
называют пределом указанной последовательности и пишут:
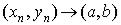 при
при 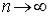 .
.
Легко показать, что  тогда и только тогда, когда одновременно
тогда и только тогда, когда одновременно  ,
, 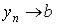 (т.е. сходимость последовательности точек пространства
(т.е. сходимость последовательности точек пространства 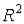 эквивалентна по координатной сходимости).
эквивалентна по координатной сходимости).
Пусть  и
и 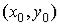 – предельная точка множества
– предельная точка множества 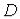 .
.
Определение. Число 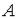 называют пределом функции
называют пределом функции 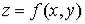 при
при 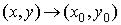 , если для
, если для
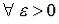
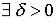 такое, что
такое, что 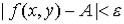 , как только
, как только 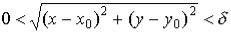 . В этом случае пишут
. В этом случае пишут
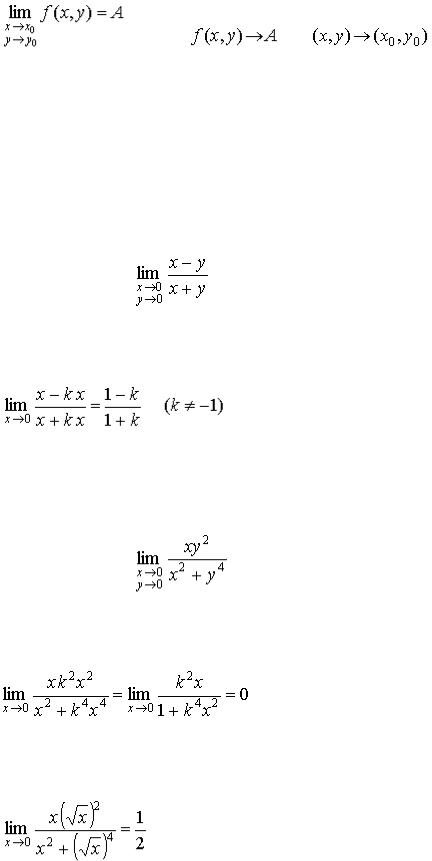
или |
при |
. |
При кажущейся полной аналогии понятий предела функций одной и двух переменных существует глубокое различие между ними. В случае функции одной переменной для существования предела в точке необходимо и достаточно равенство лишь двух чисел – пределов по двум направлениям: справа и слева от
предельной точки 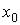 . Для функции двух переменных стремление к предельной точке
. Для функции двух переменных стремление к предельной точке 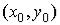 на
на
плоскости 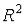 может происходить по бесконечному числу направлений (и необязательно по прямой), и потому требование существования предела у функции двух (или нескольких) переменных «жестче» по сравнению с функцией одной переменной.
может происходить по бесконечному числу направлений (и необязательно по прямой), и потому требование существования предела у функции двух (или нескольких) переменных «жестче» по сравнению с функцией одной переменной.
Пример. Найти .
 Пусть стремление к предельной точке
Пусть стремление к предельной точке 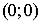 происходит по прямой
происходит по прямой 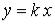 . Тогда
. Тогда
.
Предел, очевидно, не существует, так как число 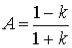 зависит от
зависит от 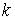 . ^
. ^
Пример. Найти .
 По любой прямой
По любой прямой 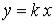 предел один и тот же:
предел один и тот же:
.
С другой стороны, пусть стремление к предельной точке происходит по кривой 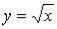 . Тогда
. Тогда
;
следовательно, предел не существует. ^
Сформулируем понятие предела функции для случая, когда предельная точка имеет бесконечные координаты. Ограничимся случаем, когда 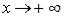 ,
, 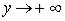 (остальное – по аналогии).
(остальное – по аналогии).

Определение. Число  называют пределом функции
называют пределом функции 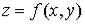 при
при 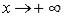 и
и 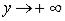 , если для
, если для 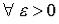
 такое, что из неравенств
такое, что из неравенств 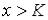 и
и 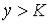 следует неравенство
следует неравенство
 . Этот факт коротко записывают так:
. Этот факт коротко записывают так:
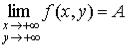 .
.
Теорема 1. Если существуют 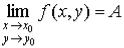 и
и 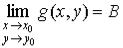 , то:
, то:
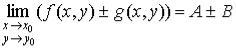 ;
;
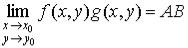 ;
;
,
где предельная точка  может быть конечной или бесконечной.
может быть конечной или бесконечной.
Справедливы аналоги и других теорем о свойствах пределов функций одной переменной.
3. Непрерывность функции. Пусть дана функция  с областью определения
с областью определения  и пусть
и пусть
 – предельная точка множества
– предельная точка множества 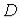 .
.
Определение. Говорят, что функция 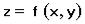 непрерывна в точке
непрерывна в точке 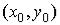 , если:
, если:
1)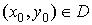 ;
;
2) |
, т.е. |
. |
Сформулируем определение непрерывности в эквивалентной форме. С этой целью обозначим
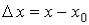 ,
, 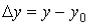 и
и 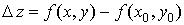 .
.
Определение. Говорят, что функция  непрерывна в точке
непрерывна в точке 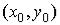 , если выполняется равенство
, если выполняется равенство
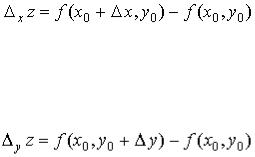
 .
.
Теорема 2. Если функции  и
и  непрерывны в точке
непрерывны в точке  , то этим же свойством обладают функции
, то этим же свойством обладают функции  ,
, 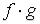 , а если
, а если 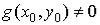 , то и функция
, то и функция 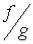 .
.
Если мы хотим ввести понятие непрерывной функции на множестве, как функции, непрерывной в каждой точке множества, то само определение непрерывности в точке требует, чтобы каждая точка
множества принадлежала ему (либо с некоторой своей 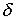 -окрестностью, либо как его граничная точка).
-окрестностью, либо как его граничная точка).
Определение. Множество 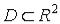 называется областью, если оно:
называется областью, если оно:
1) является открытым множеством, т.е. содержит каждую свою точку вместе с некоторой своей 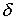 - окрестностью; 2) является линейно связным множеством, т.е. для любых двух различных точек
- окрестностью; 2) является линейно связным множеством, т.е. для любых двух различных точек
 существует ломаная, соединяющая
существует ломаная, соединяющая 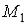 и
и  и целиком лежащая в
и целиком лежащая в 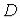 .
.
Если 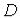 – область, то множество
– область, то множество 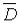 называют замкнутой областью.
называют замкнутой областью.
Определение. Говорят, что функция 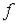 непрерывна в области
непрерывна в области 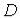 (или в замкнутой области
(или в замкнутой области  ),
),
если 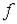 непрерывна в каждой точке этого множества.
непрерывна в каждой точке этого множества.
4. Непрерывность по отдельным переменным. Зафиксируем переменную 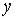 , полагая
, полагая  , а
, а
переменной  придадим произвольное приращение
придадим произвольное приращение  . Функция
. Функция 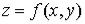 получит приращение
получит приращение
,
которое называется частным приращением функции в точке 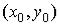 , соответствующим приращению
, соответствующим приращению 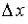 аргумента
аргумента  . Заметим, что
. Заметим, что 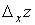 является функцией одной переменной
является функцией одной переменной 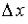 . Аналогично,
. Аналогично,
.
Определение. Функция 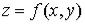 называется непрерывной в точке
называется непрерывной в точке 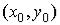 по переменной
по переменной 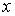
(по переменной 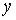 ), если
), если
 (
(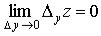 ).
).
В отличие от непрерывности по отдельным переменным обычную непрерывность функции называют иногда непрерывностью по совокупности переменных.

Теорема 3. Если функция 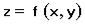 определена в некоторой окрестности точки
определена в некоторой окрестности точки 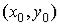 и непрерывна в этой точке, то она непрерывна в этой точке по каждой из переменных.
и непрерывна в этой точке, то она непрерывна в этой точке по каждой из переменных.
Обратное утверждение неверно.
Пример. Докажем, что функция
непрерывна в точке 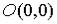 по каждой переменной
по каждой переменной  и
и  , но не является непрерывной в этой точке по совокупности переменных.
, но не является непрерывной в этой точке по совокупности переменных.
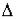 Рассмотрим частное приращение функции
Рассмотрим частное приращение функции 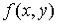 в точке
в точке  , соответствующее приращению
, соответствующее приращению 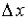 аргумента
аргумента 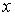 :
:
.
Очевидно, что 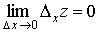 , а это означает, что
, а это означает, что  непрерывна в точке
непрерывна в точке  по переменной
по переменной
 .
.
Аналогично можно доказать непрерывность  в точке
в точке  по переменной
по переменной 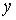 .
.
Покажем, что предел |
не существует. Пусть точка |
стремиться к точке |
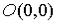 по прямой
по прямой  , проходящей через точку
, проходящей через точку 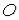 . Тогда получим
. Тогда получим
.
Таким образом, приближаясь к точке  по различным прямым, соответствующим разным значениям
по различным прямым, соответствующим разным значениям 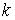 , получаем разные предельные значения. Отсюда следует, что предел данной функции в точке
, получаем разные предельные значения. Отсюда следует, что предел данной функции в точке 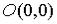 не существует, а значит, функция
не существует, а значит, функция  не является непрерывной в этой точке.
не является непрерывной в этой точке.

11. Частные производные и частные дифференциалы.
1. Частные производные первого порядка. Пусть функция 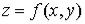 определена в области
определена в области
и |
. |
Тогда |
при |
малых |
определено |
ее |
частное |
приращение |
по : |
|
|
|
|
|
. |
|
|
|
|
|
|
|
Определение. Частной |
производной функции |
по |
переменной |
в |
точке |
|
|||
называют предел |
|
|
|
|
|
|
|
|
|
|
,
если он существует.
Частную производную по  обозначают одним из следующих символов:
обозначают одним из следующих символов:
.
Аналогично определяется частная производная по  и вводятся ее обозначения.
и вводятся ее обозначения.
Легко видеть, что частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной.
Пример. Найти частные производные функции 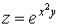 .
.
 Имеем:
Имеем:
|
|
, |
. ^ |
2. |
Частные производные |
высших порядков. Рассматривая частные |
производные |
и |
как функции от |
, приходим к понятиям частных производных второго порядка. А |
|
именно, выражения |
|
|
|
,
называют частными производными второго порядка функции 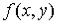 по
по 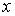 и по
и по  соответственно, а выражения
соответственно, а выражения

,
– смешанными частными производными второго порядка функции  . Их обозначают также
. Их обозначают также
символами: 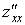 ,
, 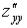 ,
, 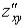 и
и 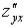 . Аналогично определяют частные производные 3-го порядка (их будет 8=23 ), 4-го порядка (их будет 16=24 ) и т.д.
. Аналогично определяют частные производные 3-го порядка (их будет 8=23 ), 4-го порядка (их будет 16=24 ) и т.д.
Теорема 4. Если в некоторой |
окрестности точки |
функция |
имеет |
|
смешанные частные производные |
и |
, причем эти производные непрерывны в точке |
, |
|
то они равны в этой точке: |
|
|
|
|
= |
. |
Если последнее равенство выполняется, то говорят, что смешанные частные производные 2-го порядка функции 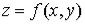 не зависят от порядка дифференцирования в точке
не зависят от порядка дифференцирования в точке  .
.
Теорема 4 допускает обобщение: по индукции ее можно распространить на любые непрерывные смешанные частные производные.
Приращение, которое получает функция Z=f(x, y), когда изменяется только одна из переменных, называется частным приращением функции по соответствующей переменной: xZ=f(x+Δx,y)-f(x,y), yZ=f(x,y+Δy)-f(x,y).
ОПРЕДЕЛЕНИЕ: Частным дифференциалом по х функции Z=f(x, y) называется главная часть частного приращения xZ=f(x+Δx,y)-f(x,y), пропорциональная приращению Δx независимой переменной х. Аналогично определяется частный дифференциал по у, т.е. yZ=f(y+Δy,x)-f(x,y).
Дифференциалы независимых переменных х и у просто равны их приращениям, т.е. dx=Δx, dy=Δy. Частные дифференциалы обозначаются так: dxZ -частный дифференциал по х, dyZ - частный дифференциал по у. При этом:
Таким образом, частный дифференциал функции двух независимых переменных равен произведению соответствующей частной производной на дифференциал этой переменной.
Таким же образом, как для функции двух переменных, определяются частные приращения и частные дифференциалы функций любого числа независимых переменных.

12. Дифференцируемость функций многих переменных.

