Билетыкэкзаменупоматематике за2семестр.1 курс.

1.Неопределенный интеграл. Первообразная.

2.Свойства неопределенного интеграла.

3.Интегрирование по частям. Замена переменной в интеграле.

4.Метод A и B – интегрирование в неопределенно-рациональных выражениях.

5.Определенный интеграл и его свойства.

6.Интеграл с переменным верхним пределом.

7.Формула Ньютона-Лейбница.

8.Интегрирование по частям и замена переменной в определенном интеграле. Основные замены.

9.Предел функции многих переменных.

10.Непрерывность функции многих переменных.

11.Частные производные и частные дифференциалы.

12.Дифференцируемость функций многих переменных.

13.Производная сложной функции.

14.I и II дифференциал и инвариантность.

15.Касательная плоскость и нормаль к поверхности.

16.Формула Тейлора.

17.Дифференциальные уравнения I порядка. Общие и частные решения. Общие понятия.

18.Дифференциальные уравнения с разделяющимися переменными.

19.Линейные дифференциальные уравнения первого порядка.

20.Понижение порядка.

21.Линейная зависимость/независимость сложных функций. Определитель Вронского.

22.Фундаментальная система решений дифференциального уравнения.

23.Линейные неоднородные уравнения с постоянными коэффициентами. (Теорема о сумме общего и частного решений.)

24.Метод Лагранжа. Вариация произвольных постоянных.

25.Связь дифференциального уравнения с системой уравнений.

26.Система дифференциальных уравнений с постоянными коэффициентами.

27.Матричный метод решения систем с постоянными коэффициентами

1. Неопределенный интеграл. Первообразная.

2. Свойства неопределенного интеграла.

Первообразная и неопределенный интеграл, их свойства.

Определение первообразной.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 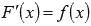для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо

равенство . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Выражение 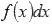называют подынтегральным выражением, а f(x) – подынтегральной функцией.

Подынтегральное выражение представляет собой дифференциал функции f(x).

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.

На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

1.Производная результата интегрирования равна подынтегральной функции.

2.Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

3. , где k – произвольная константа. Коэффициент можно выносить за знак неопределенного интеграла.

4.Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.

Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:

Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.

Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:

•первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;

•второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.

3. Интегрирование по частям. Замена переменной в интеграле.

Метод интегрирования по частям позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу. Этот метод наиболее часто применяется, если подынтегральная функция содержит логарифмические, показательные, обратные тригонометрические, тригонометрические функции, а также их комбинации.

Формула интегрирования по частям следующая

.

То есть, подынтегральное выражение f(x)dx представляем в виде произведения функции u(x)на d(v(x)) - дифференциал функции v(x). Далее находим функцию v(x) (чаще всего методом непосредственного интегрирования) и d(u(x)) - дифференциал функции u(x). Подставляем найденные выражения в формулу интегрирования по частям и исходный неопределенный интеграл сводится к разности

. Последний неопределенный интеграл может быть взят с использованием любого метода интегрирования, в том числе и метода интегрирования по частям.

В качестве примера найдем множество первообразных функции логарифма.

Пример.

Найти неопределенный интеграл

Решение.

Найдем этот неопределенный интеграл методом интегрирования по частям. В качестве

функции u(x) возьмем ln(x), а в качестве d(v(x)) оставшуюся часть подынтегрального выражения, то есть dx.

Имеем, 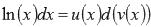, где .

Дифференциал функции u(x) есть , а функция v(x) – это

.

ЗАМЕЧАНИЕ: константу С при нахождении функции v(x) считают равной нулю.

Теперь все подставляем в формулу интегрирования по частям:

Ответ:

Подведение под знак дифференциала

Данный метод эквивалентен методу замены переменной (см. далее):