
- •Задачник-практикум по линейной алгебре
- •Введение
- •1. Матрицы. Операции с матрицами
- •Задания для самостоятельной работы по теме
- •Задания для самостоятельной работы по теме
- •Задания для самостоятельной работы по теме
- •Задания для самостоятельной работы по теме
- •5.1. Метод Гаусса
- •5.2. Матричный метод решения систем линейных уравнений
- •5.3. Метод Крамера
- •6. Исследование систем линейных уравнений.
- •Задания для самостоятельной работы по теме
- •Библиографический список
- •Оглавление
- •Задачник-практикум по линейной алгебре
- •Отпечатано методом прямого репродуцирования
- •6 80021, Г. Хабаровск, ул. Серышева, 47.
1. Матрицы. Операции с матрицами
Определение
1.1.
Числовой матрицей
размера mn,
где m
– число строк, n
– число столбцов, называется таблица
чисел, расположенных в определённом
порядке. Эти числа называются элементами
матрицы. Место каждого элемента
![]() однозначно определяется номером строкиi
и номером столбца j,
на пересечении которых он находится:
однозначно определяется номером строкиi
и номером столбца j,
на пересечении которых он находится:

Иногда
коротко пишут
![]() т. е.i
меняется от 1 до m,
j
– от 1 до n.
т. е.i
меняется от 1 до m,
j
– от 1 до n.
Замечание.
Матрица размерностью
![]() состоит из одного элемента и равна этому
элементу.
состоит из одного элемента и равна этому
элементу.
Далее рассмотрим специальные виды матриц.
Определение
1.2.
Матрицей-строкой (строчечной матрицей)
называется матрица
![]() размерности
размерности![]() ,
состоящая из одной строки:
,
состоящая из одной строки:
![]()
Определение
1.3.
Матрицей-столбцом (столбцевой матрицей,
числовым вектором) называется матрица
![]() размерности
размерности![]() ,
состоящая из одного столбца:
,
состоящая из одного столбца:

Определение
1.4.
Квадратной матрицей порядка
![]() называется матрица, у которой число
строк и число столбцов одинаково и равно
называется матрица, у которой число
строк и число столбцов одинаково и равно![]()

Элементы
матрицы, расположенные на главной
диагонали матрицы, имеют одинаковые
индексы строки и столбца:
![]()
Определение
1.5.
Единичной
матрицей
![]() называется квадратная матрица, у которой
все элементы главной диагонали равны
единице, а все остальные элементы –
нулю:
называется квадратная матрица, у которой
все элементы главной диагонали равны
единице, а все остальные элементы –
нулю:

Определение
1.6.
Если в квадратной матрице
![]() ,
то матрица называется симметричной.
,
то матрица называется симметричной.
Пример.
 симметричная
матрица.
симметричная
матрица.
Определение 1.7. Квадратная матрица вида

называется диагональной матрицей.
С матрицами можно выполнять следующие операции: сложение, умножение на число, умножение матриц, транспонирование.
Определение
1.8.
Суммой двух матриц
![]() и
и![]() одной размерности называется такая
третья матрица
одной размерности называется такая
третья матрица![]() той же размерности, что и матрицы–слагаемые,
каждый элемент которой
той же размерности, что и матрицы–слагаемые,
каждый элемент которой![]() представляет собой сумму соответствующих
элементов матриц
представляет собой сумму соответствующих
элементов матриц![]() и
и![]() :
:
![]() .
.
Определение
1.9.
Произведением матрицы
![]() на действительное число
на действительное число![]() называется такая матрица
называется такая матрица![]() той же размерности, что и матрица
той же размерности, что и матрица![]() каждый элемент которой
каждый элемент которой![]() представляет собой произведение
соответствующего элемента матрицы
представляет собой произведение
соответствующего элемента матрицы![]() на число
на число![]() :
:
![]()
Пример. Даны матрицы
 ;
;
 ,
,
найти
матрицу
![]()
Пользуясь определениями 1.8 и 1.9, получим следующие матрицы:


Определение
1.10.
Произведением матрицы
![]() размерности
размерности![]() с матрицей
с матрицей![]() размерности
размерности![]() в указанном порядке называется такая
третья матрица
в указанном порядке называется такая
третья матрица![]() размерности
размерности![]() каждый элемент которой
каждый элемент которой![]() представляет собой сумму произведений
соответствующих элементов
представляет собой сумму произведений
соответствующих элементов![]() й
строки матрицы
й
строки матрицы![]() и
и![]() го
столбца матрицы
го
столбца матрицы![]() :
:
![]() .
.
Замечание. Из определения 1.10 следует, что перемножать можно только те матрицы, у которых число столбцов первого множителя равно числу строк второго.
Определение
1.11.
Матрица
![]() размерности
размерности![]() называется транспонированной по
отношению к матрице
называется транспонированной по
отношению к матрице![]() размерности
размерности![]() ,
если она получена из неё заменой строк
столбцами (или, что то же, столбцов –
строками):
,
если она получена из неё заменой строк
столбцами (или, что то же, столбцов –
строками):

Пример. Даны матрицы


Составить
матрицу
![]()
Пользуясь определениями 1.10 и 1.11, получим матрицы
 ;
;

Пример. Найти произведение матриц
 и
и
![]() .
.
По
определению 1.10, результатом перемножения
матриц
![]() и
и![]() будет матрица размерности
будет матрица размерности![]() а при перемножении матриц
а при перемножении матриц![]() и
и![]() получится матрица размерности
получится матрица размерности![]()


![]()
Пример. Найти произведение матриц
![]() и
и![]()
По
определению 1.10, результатом перемножения
матриц
![]() и
и![]() будет матрица размерности
будет матрица размерности![]()
![]()
Пример. Дана матрица
![]()
Записать
матрицу
![]()
Воспользуемся определением 1.10 и запишем:
![]()
![]()
![]()
Теорема 1.1. Операции с матрицами обладают следующими основными свойствами:
 –коммутативность
сложения матриц.
–коммутативность
сложения матриц. –ассоциативность
сложения матриц.
–ассоциативность
сложения матриц. –произведение
матриц в общем случае некоммутативно.
–произведение
матриц в общем случае некоммутативно. –ассоциативность
произведения матриц.
–ассоциативность
произведения матриц. –дистрибутивность
умножения матрицы на число относительно
сложения действительных чисел
–дистрибутивность
умножения матрицы на число относительно
сложения действительных чисел

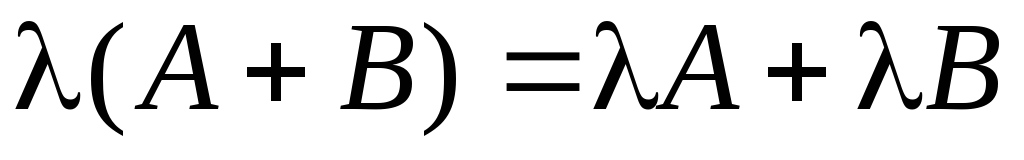 –дистрибутивность
умножения матрицы на действительное
число
–дистрибутивность
умножения матрицы на действительное
число
 относительно сложения матриц.
относительно сложения матриц. –двойное
транспонирование матрицы имеет своим
результатом исходную матрицу.
–двойное
транспонирование матрицы имеет своим
результатом исходную матрицу. если
эти произведения имеют смысл.
если
эти произведения имеют смысл.
