Зависимость числа интервалов от объема выборки
|
n |
До 50 |
50 — 100 |
100 — 500 |
500 — 1000 |
Свыше 1000 |
|
k |
6 — 8 |
8-10 |
10-13 |
13-15 |
15-20 |
При этом желательно, чтобы в каждом интервале было не менее восьми наблюдений (в крайних интервалах число наблюдений может быть меньше восьми).
Для нашего примера принимаем k = 8. Определяем ширину интервала (h) по формуле
h =
=
=
15,8/8=
1,975
Принимаем h = 2,0, условно считаем Хmax = 16,0. Записываем статистический ряд по интервалам (табл. 3.3). Эмпирической функцией распределения Fn(х) называют функцию накопленных (кумулятивных) частостей, для нашего примера она имеет вид Рис. 3.3.
Функция Fn(х) может быть изображена графически (см. рис. 3.3) в координатах (х, Fn(х)). Функция Fn(х) служит оценкой неизвестной функции распре- деления F(x) для случайной величины х.
Таблица 3.3
Статистический ряд по интервалам
-
Номер интер- вала i
Интервал значений для хi.
Среднее значение х в ин- тервале, хi*.
Частота наблюде- ний в интервале, mi.
Частость,
wi
Накоп- ленная частость, wn,i
1
0 ≤ х1 ≤ 2
1
6
0,09375
0,09375
2
2 ≤ х2 ≤ 4
3
8
0,12500
0,21875
3
4 ≤ x3 ≤ 6
5
10
0,15625
0,37500
4
6 ≤ х4 ≤ 8
7
12
0,18750
0,56250
5
8 ≤ x5 ≤ 10
9
10
0,15625
0,71875
6
10 ≤ х6 ≤12
11
8
0,12500
0,84375
7
12 ≤ х7 ≤ 14
13
6
0,09375
0,93750
8
14 ≤ х8 ≤ 16
15
4
0,06250
1,00000
Сумма
64
1,00000
1,00000
Можно получить выборочную функцию распределения плотности вероятностей fn(х) в сере- дине интервалов хi* (см. ниже рис. 2.3)
fn(хi*)= mi /nh,
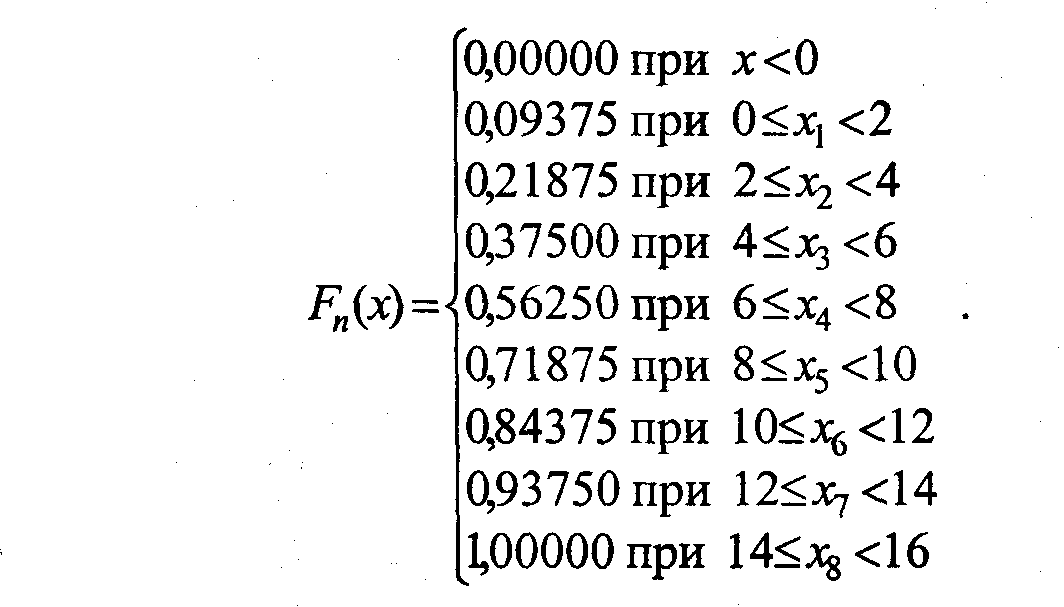
Рис. 3.3. Эмпирическая функция распределения нитратов в огурцах.
Например, для первого интервала
fn(xi*)
=
= 0,046875
Тогда f'n(х) для нашего примера будет иметь следующий вид:
⌠ 0,00000 при х < 0
│ 0,04687 при 0 < x1 < 2
│ 0,06250 при 2 < х2 < 4
│ 0,07823 при 4 < х3 < 6 130
fn(x) = { 0,09375 при 6 < х4 < 8
│ 0,07812 при 8 < х5 <10
│ 0,06250 при 10 < х6 < 12
│ 0,04687 при 12 < х7 <14
⌡ 0,03125 при 14 < х8 <16
Если генеральная совокупность N обладает двумерным признаком Х и Y, где Х и Y представляют собой случайные зависимые величины, то статистический ряд может иметь вид, приведенный:
в табл. 2.4 (когда обе величины Х и Y непрерывны); табл. 2.5 (Х непрерывна, а Y дискретна); табл. 2.6 (обе Х и Y дискретны).
В табл. (2.4 - 2.6) частота наблюдений mij показывает, сколько встречается в опыте пар (хi,уj).
Таблица 3.4
Статистический ряд при непрерывных величинах Х и Y
-
Х
Y
Границы интервала
0,1<у1<2
0,2<у2<0,3
0,3<у3<0,4
0,4<у4<0,5
Грани- цы
интер- вала
0 ≤ х1< 1,1
m11= 5
m12 = 4
m13= 3
m14= 1
1,1≤х2< 2,2
m21= 1
m22= 7
m23= 6
m24= 4
2,2 ≤x3<3,3
m31 = 0
m32 = 8
m33= 5
m34 = 2
2,2 ≤x3<3,3
m41= 2
m42= 4
m43= 1
m44= 3
Таблица 3.5
Статистический ряд, когда Х непрерывна, а Y дискретна
|
Y X |
Значение у,. | ||||
|
y1= 2 |
y2 = 4 |
y3 = 6 |
y4 = 8 | ||
|
Грани- цы интер- вала |
0,5≤ х2<1,5 |
m11= 4 |
m12=6 |
m13=4 |
m14= 2 |
|
1,5≤ х2<2,5 |
m21= 3 |
m22=5 |
m23=6 |
m24=5 | |
|
2,5≤ х2<3,5 |
m31= 1 |
m32= 5 |
m33=4 |
m34=7 | |
Таблица 3.6
Статистический ряд, когда Х и Y дискретны
|
У Х |
Значение у,. | |||||
|
1 |
2 |
3 |
4 |
5 | ||
|
|
.10 |
m»= 5 |
т,,=4 |
m»= 8 |
т — 7 |
т =2 1з |
|
Значе- |
15 |
т,,=2 |
изб |
и,,=4 |
т4= 3 |
и,,= 2 |
|
ние х,. |
20 |
т =1 зз |
т,,=6 |
m»= 5 |
и =1 з~ |
тзз 2 |
|
|
25 |
m4) 3 |
т =3 42 |
т,,=4 |
т =5 44 |
т,,=6 |
Если генеральная совокупность N обладает р-мерным признаком
(L = l, 2,...,1,..., р), где x1, x2, x3, …, xn, …, хp — случайные величины, то статистический ряд будет состоять при выборке n из n векторов
(x11, x21, x31, …, xn1)
(x12, x22, x32, …, xn2)
…………………….
(x1n, x2n, x3n, …, xnm)
где хij — случайная величина хj в i-ом испытании (наблюдении).
Результаты наблюдений могут быть также представлены в виде матрицы
X =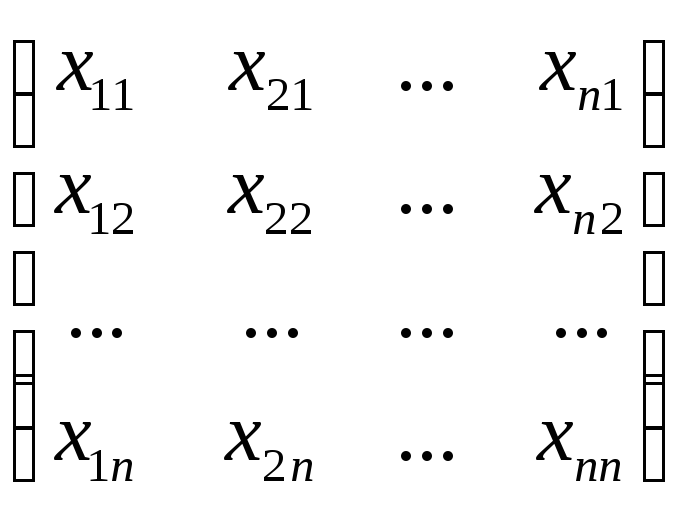
назад