
- •В.М. Полунин, г.Т.Сычев
- •Физические основы механики
- •Конспект лекций
- •Содержание
- •От авторов
- •Лекция 1. Вводная
- •Лекция 2. Элементы кинематики
- •2.1. Механика и ее разделы. Физические модели: материальная точка (частица), абсолютно твердое тело (система материальных точек), сплошная среда
- •2.2. Пространственно-временные отношения. Развитие представлений о свойствах пространства и времени в механике
- •2.3. Системы отсчета и описание движений. Элементы кинематики материальной точки: перемещение, скорость и ускорение
- •2.4. Элементы кинематики материальной точки и тела, совершающих вращательное движение: угол поворота, угловые скорость и ускорение. Их связь с линейной скоростью и линейным ускорением
- •2.5. Гармонические колебательные движения и их характеристики: смещение, амплитуда, период, частота, фаза, скорость и ускорение
- •2.6. Методы сложения гармонических колебаний. Векторные диаграммы. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения
- •2.7. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу
- •Лекция 3.Элементы динамики материальной точки и твердого тела
- •3.2. Инерциальные и неинерциальные системы отсчета
- •3.3. Описание движения в неинерциальных системах отсчета
- •3.3.1. Силы инерции при ускоренном движении системы отсчета
- •3.3.2. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета
- •3.3.3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета (сила Кориолиса)
- •Силы инерции, возникающие в неинерциальной системе отсчета в зависимости от состояния частицы
- •3.5. Основной закон динамики вращательного движения
- •3.6. Сопоставление формул динамики вращательного и динамики поступательного движений
- •Сопоставление формул динамики поступательного движения и динамики вращательного движения
- •Лекция 4. Физика колебаний. Гармонический осциллятор. Нормальные моды
- •4.1. Дифференциальное уравнение гармонических колебаний и его решение
- •4.2. Примеры гармонических осцилляторов. Физический, математический и пружинный маятники. Определение их периодов и частот
- •4.2.1. Пружинный маятник
- •4.2.2. Физический и математический маятники
- •4.3. Свободные (затухающие колебания). Дифференциальное уравнение затухающих колебаний и его решение. Характеристики затухающих колебаний
- •4.4. Вынужденные колебания гармонического осциллятора под действием синусоидальной силы. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний
- •Лекция 5.Ангармонические колебания
- •5.1. Нелинейный осциллятор. Физические системы, содержащие нелинейность
- •5.2. Автоколебания. Обратная связь. Условие самовозбуждения. Роль нелинейности. Предельные циклы
- •Лекция 6. Физика волн. Волновые процессы
- •6.1. Кинематика и динамика волновых процессов. Плоская стационарная и синусоидальная волна
- •6.2. Уравнение плоской волны
- •6.3.Волновое уравнение
- •6.4. Интерференция волн. Стоячие волны
- •Лекция 7.Энергия, работа, мощность
- •7.1. Работа силы и её выражение через криволинейный интеграл
- •Из (7.1) следует, что при
- •7.1.1. Работа, совершаемая внешними силами при вращательном движении относительно неподвижной оси
- •7.2. Мощность
- •Различают мгновенную мощность и среднюю мощность.
- •Поскольку
- •7.3. Энергия как универсальная мера различных форм движений и взаимодействий
- •7.4. Кинетическая энергия системы и её связь с работой внешних и внутренних сил, приложенных к системе
- •7.5. Энергия системы, совершающей вращательное движение
- •Подставив значение VI в (7.35) будем иметь
- •То есть работа внешних сил, действующих на вращающуюся относительно неподвижной оси материальную точку (тело, систему), равна изменению кинетической энергии:
- •7.6. Потенциальная энергия и энергия взаимодействия. Потенциальная энергия и устойчивость системы
- •7.6.1. Связь между потенциальной энергией и силой
- •7.6.2. Внутренняя энергия
- •7.6.3. Силовые поля. Поле как форма существования материи. Поле как форма существования материи осуществляющая силовое взаимодействие между материальными объектами. Характеристики силовых полей
- •Второй характеристикой силового потенциального поля является потенциал.
- •7.6.4. Потенциальная энергия материальной точки (тела, системы) во внешнем силовом поле
- •7.6.5. Поле центральных сил. Движение в поле центральных сил
- •Элементарная работа по перемещению массы на элементарном отрезке dr:
- •Из полученного соотношения видно:
- •В случае, когда сила притяжения будет равна центростремительной силе, то
- •Подставляя значения vа и vп в формулу (7.41), будем иметь
- •Подставив в формулу (7.83) значения r и V, будем иметь t 92 мин.
- •7.7. Энергия упругой деформации
- •7.8. Энергия системы, совершающей колебательное движение
- •Кинетическая энергия системы, совершающей гармоническое колебание, находится по формуле
- •Лекция 8. Законы сохранения в механике
- •8.1. Закон сохранения энергии в механике
- •8.1.1. Общефизический закон сохранения энергии
- •8.1.2. Закон сохранения и превращения механической энергии
- •8.2. Закон сохранения импульса. Центр инерции. Закон движения центра инерции
- •8.3. Закон сохранения момента импульса. Уравнение моментов
- •В векторной форме
- •8.4. Применение законов сохранения к упругому и неупругому взаимодействиям (удару)
- •8.4.1. Абсолютно неупругий удар шаров
- •Лекция 9. Основы релятивистской механики. Релятивистская кинематика
- •9.1. Принцип относительности Галилея. Преобразования Галилея. Инварианты преобразования. Закон сложения скоростей в классической механике
- •9.2. Постулаты и представления о свойствах пространства и времени в специальной теории относительности
- •9.3. Преобразования Лоренца для координат и времени
- •9.4. Следствия из преобразований Лоренца
- •9.4.1. Закон сложения скоростей в теории относительности
- •9.4.2. Сокращение движущихся масштабов длин
- •9.4.3.Замедление хода движущихся часов
- •Лекция 10.Релятивистская динамика
- •10.2. Четырехмерное пространство - время. Преобразования в четырехмерном пространстве
- •10.2.1. Основные понятия
- •10.2.2. Кинематика четырехмерного пространства-времени
- •10.2.3. Динамика четырехмерного пространства-времени
- •10.3. Столкновения релятивистских частиц. Законы сохранения энергии и импульса
- •10.4. Значение теории относительности
- •Библиографический список Основной
- •Дополнительный
- •Физика Физические основы механики Конспект лекций
2.6. Методы сложения гармонических колебаний. Векторные диаграммы. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения
Колебания, совершаемые материальными точками, телами, системами, чаще всего являются результатом сложения нескольких гармонических колебаний, совершаемых одновременно. Следовательно, любое сложное колебание можно разложить на несколько простых (гармонических). Для того чтобы знать, как зависит характер сложного колебания от соотношения фаз, частот, амплитуд и направлений складываемых колебаний, рассмотрим наиболее простые случаи сложения гармонических колебаний. Основными методами сложения колебаний являются метод векторных диаграмм и аналитический метод.
М етод
векторных диаграмм заключается в том,
что гармонические колебания изображаются
графически в виде вектора на плоскости.
Для этого из начала координат на
плоскости проводят вектор, модуль
которого равен амплитуде рассматриваемых
колебаний, который составляет с осью
координат (горизонтальной осью) угол
= t
+ 0,
равный фазе колебаний в данный момент
времени t (рис.2.7).
етод
векторных диаграмм заключается в том,
что гармонические колебания изображаются
графически в виде вектора на плоскости.
Для этого из начала координат на
плоскости проводят вектор, модуль
которого равен амплитуде рассматриваемых
колебаний, который составляет с осью
координат (горизонтальной осью) угол
= t
+ 0,
равный фазе колебаний в данный момент
времени t (рис.2.7).
С течением времени угол увеличивается так, что вектор равномерно вращается относительно начала координат с угловой скоростью, равной циклической частоте . Соответственно проекция вектора на вертикальную ось совершает гармонические колебания по закону:
![]() (2.28)
(2.28)
Этим методом широко пользуются при сложении одинаково направленных гармонических колебаний.
Предположим, что имеются два гармонических колебания с одинаковой частотой 1 = 2 = (T1 = T2 = T), но с разными амплитудами x01 x02 и начальными фазами 01 02. Уравнения таких колебаний будут иметь вид:
x1 = x01sin(t + 01); x2 = x02sin(t + 02). (2.29)
Изобразив эти колебания в виде векторной диаграммы, для амплитуды результирующего колебания получим:
x0 = x01 + x02. (2.30)
Численное значение амплитуды результирующего колебания можно определить по теореме косинусов:
x02 = x012 + x022 - 2x01x02cos[ - (1 - 2)] =
= x012 + x022 - 2x01x02cos(1 - 2)]. (2.31)
Пользуясь векторной диаграммой, определяем начальную фазу результирующего колебания:
![]() (2.32)
(2.32)
Уравнение результирующего колебания будет иметь вид
![]() (2.33)
(2.33)
Анализ полученного результата приводит к следующим выводам:
1. При 01 - 02 = 2k - разность начальных фаз складываемых колебаний равна четному числу ; в частности при k = 0, (01 - 02 = 0):
x0 = x01 + x02; tg0 = tg01 = tg02; 0 = 01 = 02. (2.34)
Колебания синфазные и усиливают друг друга.
2. При 01 - 02 = (2k + 1) - разность начальных фаз складываемых колебаний равна нечетному числу ; в частности при k = 0, (01 - 02) = :
x0 = x01 – x02; 01 = -02. (2.35)
Колебания противофазные и ослабляют друг друга.
3. При x01 = x02; 1 = 2 = ; 02 01. Уравнения таких гармонических колебаний имеют вид
![]() (2.36)
(2.36)
![]() (2.37)
(2.37)
Для получения уравнения результирующего колебания воспользуемся аналитическим методом сложения колебаний. В этом случае будем иметь
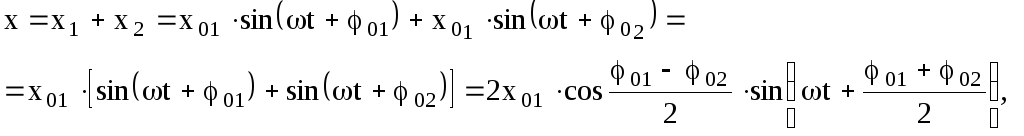
(2.38)
где
![]()
![]() - амплитуда результирующего колебания;
- амплитуда результирующего колебания;
![]() -
фаза результирующего колебания.
-
фаза результирующего колебания.
Результирующее колебание - гармоническое, такой же частоты, отличающееся по фазе от складываемых колебаний на половину суммы их начальных фаз.
Из полученного результата видно, что:
а) при 01 - 02 = 2k - разность начальных фаз складываемых колебаний равна четному числу ; в частности при k = 0 (01 - 02 = 0):
x0 = 2x01. (2.39)
Колебания усиливают друг друга;
б) при 01 - 02 = (2k + 1) - разность начальных фаз складываемых колебаний равна нечетному числу ; в частности при k=0 (01 - 02 = ):
x0 = x02 – x01 = 0. (2.40)
Колебания гасят друг друга. В остальных случаях амплитуда результирующего колебания меньше суммы амплитуд складываемых колебаний.
Особый интерес представляет сложение колебаний одного направления, амплитуды которых одинаковы (x02 = x01); начальные фазы равны 0 (01=02=0), а круговые частоты мало отличаются друг от друга (1 2). Уравнения таких колебаний имеют вид
x1 = x01sin1t; x2 = x01sin2t. (2.41)
Уравнение результирующего колебания запишем, если воспользуемся аналитическим методом сложения гармонических колебаний:
x
= x1
+ x2
= x01sin1t
+ x01sin2t
= 2x01![]() , (2.42)
, (2.42)
где
![]() - амплитуда результирующего колебания,
которая зависит от
= 1
- 2
– разности частот складываемых
колебаний.
- амплитуда результирующего колебания,
которая зависит от
= 1
- 2
– разности частот складываемых
колебаний.
![]() -
смещение результирующего колебания,
изменяющееся по гармоническому закону.
-
смещение результирующего колебания,
изменяющееся по гармоническому закону.
Так
как
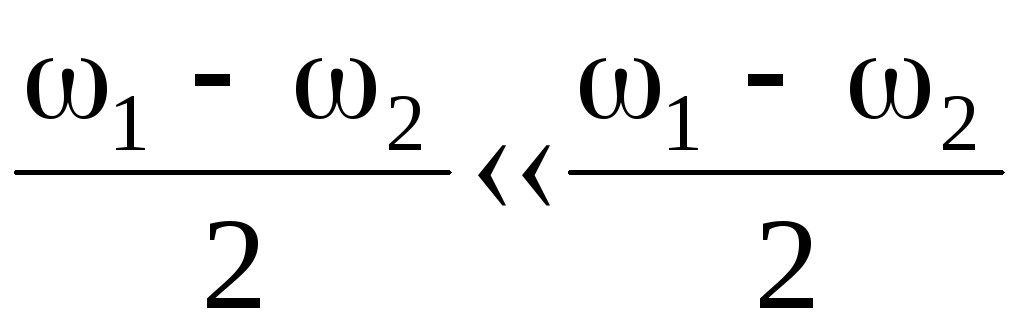 ,
то амплитуда результирующего колебания
изменяется со временем медленнее, чем
смещение. Поэтому результирующее
колебание можно считать почти
гармоническим. Частота и период
результирующего колебания соответственно
будут равны
,
то амплитуда результирующего колебания
изменяется со временем медленнее, чем
смещение. Поэтому результирующее
колебание можно считать почти
гармоническим. Частота и период
результирующего колебания соответственно
будут равны
![]() (2.43)
(2.43)
Частота и период изменения амплитуды (частота и период биения):
![]() (2.44)
(2.44)
Такие колебания называются биениями.
Рис.2.8
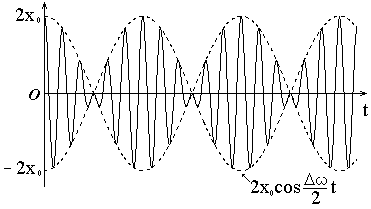
Периодическое
изменение амплитуды от
![]() до
до![]() обусловлено постепенным запаздыванием
по фазе одного из исходных колебаний:
при разности фаз исходных колебаний,
равной
обусловлено постепенным запаздыванием
по фазе одного из исходных колебаний:
при разности фаз исходных колебаний,
равной![]() (где
(где![]() ),
амплитуда результирующего колебания
равна
),
амплитуда результирующего колебания
равна![]() ,
а при разности фаз, равной
,
а при разности фаз, равной![]() (где
(где![]() ),
амплитуда равна
),
амплитуда равна![]() .
.
Одним из применений получения биений является настройка музыкальных инструментов. Настройщик рояля, например, добивается "нулевых" биений звуковых колебаний от эталонных камертонов и струн музыкального инструмента (постепенно натягивая или отпуская струну, он добивается максимального снижения частоты результирующего звукового колебания, благодаря чему процесс настройки становится стандартным и очень точным). В так называемых "гетеродинных" частотомерах также используется принцип нулевых биений для идентификации частоты нового источника колебаний.
В результате сложения гармонических колебаний, совпадающих по направлению и имеющих кратные циклические частоты , 2, 3 и т.д., получаются периодические негармонические колебания с периодом T = 2/. В свою очередь, любое сложное периодическое колебание x = f(t) можно представить в виде суммы простых гармонических колебаний с циклическими частотами, кратными основной циклической частоте = 2/T, где T - период колебаний:
![]() (2.45)
(2.45)
где
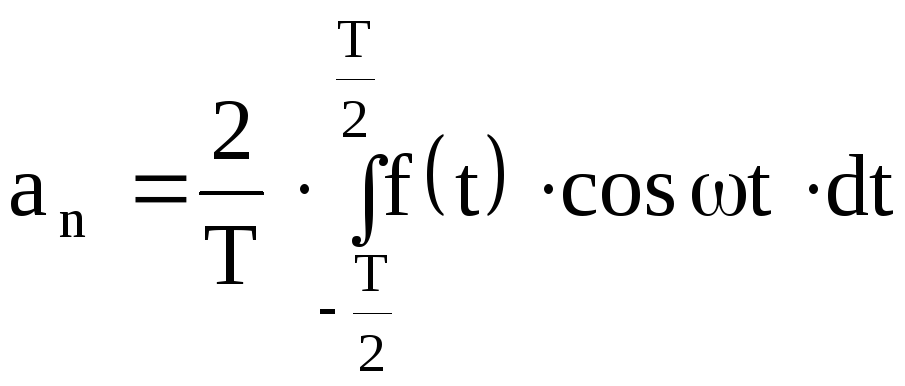 ,
при (n
= 0, 1, 2, …..);
,
при (n
= 0, 1, 2, …..);
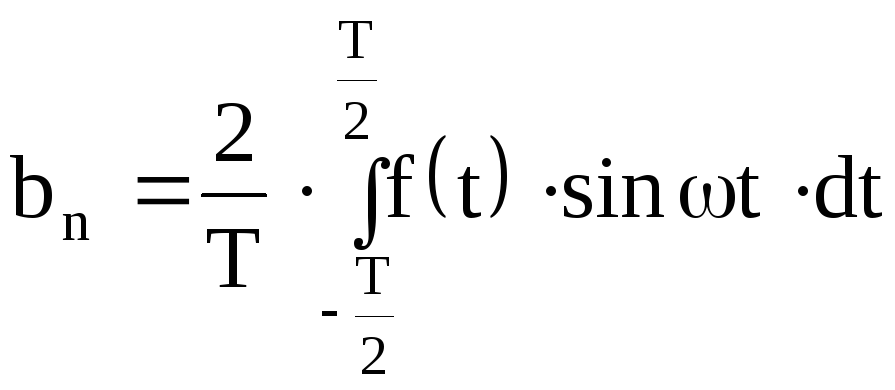 ,
при (n
= 1, 2, …..).
,
при (n
= 1, 2, …..).
Такое представление периодической функции f(t) называется разложением этой функции в ряд Фурье или гармоническим анализом сложного периодического колебания. Члены ряда Фурье, соответствующие гармоническим колебаниям с циклическими частотами , 2, 3 и т.д., называются первой, или основной, второй, третьей и т.д. гармониками сложного периодического колебания x = f(t). Совокупность этих гармоник образует спектр колебания x = f(t). Состав спектра зависит от вида периодической функции x = f(t). В простейших случаях спектр может состоять из небольшого числа гармоник.
Часто под спектром колебания понимают спектр его частот, т.е. совокупность частот простых гармонических колебаний, в результате сложения которых может быть получено рассматриваемое сложное колебание. Периодические колебания имеют дискретные (линейчатые) спектры частот.
