- •Глава 12. Функциональные ряды
- •12.1. Сходимость функциональных последовательностей и рядов
- •11.2. Функциональные свойства предельной функции и суммы ряда
- •11.3. Степенные ряды
- •11.4. Ряд Тейлора
- •11.5. Тригонометрические ряды Фурье
- •11.6. Свойства коэффициентов Фурье
- •11.7. Сходимость ряда Фурье
- •11.8. Тригонометрические ряды в комплексной форме
- •11.9. Интеграл Фурье
- •11.10. Контрольные вопросы
- •11.11. Задачи для самостоятельного решения.
11.4. Ряд Тейлора
Пусть функция
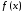 является суммой степенного ряда
является суммой степенного ряда
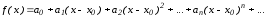 ,
(15)
,
(15)
интервал
сходимости которого есть
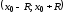 .
.
Найдем коэффициенты
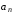 .
В интервале сходимости ряд можно почленно
дифференцировать, причем получится
ряд, сходящийся в этом интервале.
Продифференцируем последовательно ряд
.
В интервале сходимости ряд можно почленно
дифференцировать, причем получится
ряд, сходящийся в этом интервале.
Продифференцируем последовательно ряд раз
раз
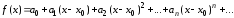 ,
,
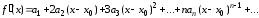 ,
,
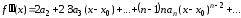 ,
,
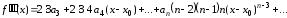
. . . . . . . . . . . . . . . . . . . . . .
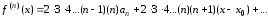
Положим
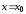 в этих тождествах.
в этих тождествах.
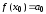 ;
;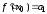 ;
;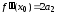 ;
;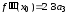 ;
;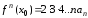 .
.
Откуда коэффициенты ряда
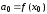 ,
,
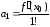 ,
,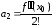 ,…,
,…,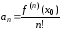 .
.
Подставляя в (15) получим ряд
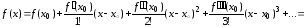
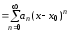 (16)
(16)
Полученный
ряд (16) называется рядом
Тейлора для
функции
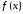 .
.
В частности, если
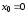 ,
то этот ряд называетсярядом
Маклорена.
,
то этот ряд называетсярядом
Маклорена.
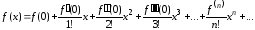
Таким образом,
если степенной ряд
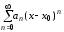 имеет сумму
имеет сумму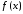 ,
то коэффициенты этого ряда определяются
по формулам
,
то коэффициенты этого ряда определяются
по формулам
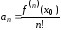 ,
,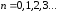 (17)
(17)
В этом случае
говорят, что функция
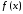 разлагается в степенной ряд в окрестности
точки
разлагается в степенной ряд в окрестности
точки
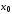 или по степеням
или по степеням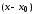 .
Очевидно, что ряд Тейлора является
бесконечным продолжением формулы
Тейлора.
.
Очевидно, что ряд Тейлора является
бесконечным продолжением формулы
Тейлора.
Ясно, что если
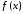 разлагается в степенной ряд (т.е. является
суммой степенного ряда), то она
разлагается в степенной ряд (т.е. является
суммой степенного ряда), то она число раз дифференцируема.
число раз дифференцируема.
Поставим обратную
задачу. Пусть
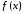 –бесконечное
число раз дифференцируемая функция в
точке
–бесконечное
число раз дифференцируемая функция в
точке
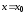 .
Составим для нее формально ряд Тейлора
(16), т.е. найдем коэффициенты
.
Составим для нее формально ряд Тейлора
(16), т.е. найдем коэффициенты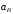 по формулам (17). Возникает вопрос: будет
ли сумма данного ряда Тейлора совпадать
с функцией
по формулам (17). Возникает вопрос: будет
ли сумма данного ряда Тейлора совпадать
с функцией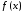 ,
для которой он составлен?
,
для которой он составлен?
Теорема
12. Для того
чтобы бесконечно дифференцируемая
функция в окрестности точки
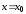 являлась суммой составленного для нее
ряда Тейлора необходимо и достаточно,
что бы остаточный ряд
являлась суммой составленного для нее
ряда Тейлора необходимо и достаточно,
что бы остаточный ряд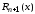 в формуле Тейлора для функции
в формуле Тейлора для функции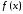 в окрестности точки
в окрестности точки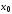 стремится к 0 при
стремится к 0 при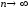 ,
т.е.
,
т.е.
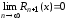 (18)
(18)
Запишем формулу Тейлора в окрестности
точки

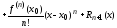 ,
,
где
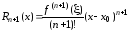 ,
,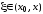 остаточный член в формуле Лагранжа.
остаточный член в формуле Лагранжа.
Ясно, что ряд Тейлора представляет собой бесконечное удлинение функции Тейлора.
Необходимость. Обозначим частичную сумму ряда
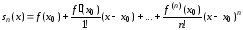 .
.
Тогда
из формулы Тейлора получаем
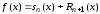 ,
,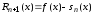 .
.
Пусть
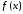 – сумма ряда Тейлора, т.е.
– сумма ряда Тейлора, т.е.
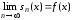 .
Тогда из
.
Тогда из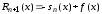 ,
,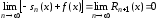 .
.
Достаточность.
Пусть,
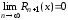 .
Из
.
Из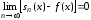 следует, что
следует, что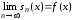 ,
т.е.
,
т.е.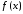 является суммой ряда Тейлора.<
является суммой ряда Тейлора.<
Непосредственная
проверка выполнения условия (18) обычно
бывает довольно сложной. Сформулируем
достаточное условие сходимости ряда
(16) к
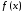 .
.
Теорема 13.
Пусть функция
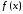 бесконечное число раз дифференцируемая
в некоторой окрестности точки
бесконечное число раз дифференцируемая
в некоторой окрестности точки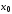 и
и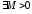 ,
что выполняется
,
что выполняется
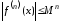 ,
,
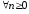 и
и
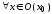 , (19)
, (19)
тогда
ряд (16) сходится к
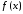 .
.
Надо показать, что при сделанных предположениях в теореме выполняется условие (18). Из формулы
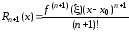
следует,
что
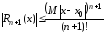 .
Но
.
Но
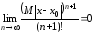 (известно из теоремы пределов). Тогда
условие (18) выполняется и из теоремы 12
следует, что теорема доказана.<
(известно из теоремы пределов). Тогда
условие (18) выполняется и из теоремы 12
следует, что теорема доказана.<
Следствие.
Пусть все
производные
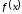 ограничены
в совокупности в интервале
ограничены
в совокупности в интервале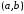 и
и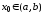 ,
т.е.
,
т.е.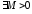 ,
что выполнится
,
что выполнится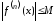 для
для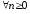 и
и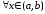 .
Тогда ряд Тейлора сходится к
.
Тогда ряд Тейлора сходится к
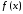 на
на
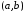 .
.
Заметим , что ряд Тейлора не всегда сходится к той функции, для которой он написан.
Пример
16.(Адамар)
Функция
 бесконечное число раз дифференцируема.
Если
бесконечное число раз дифференцируема.
Если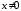 ,
то
,
то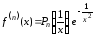 и
функция, очевидно, дифференцируемая.
При
и
функция, очевидно, дифференцируемая.
При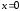 производные вычисляются по определению,
причем
производные вычисляются по определению,
причем
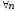 .
Отсюда
.
Отсюда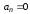 и ясно, что полученный ряд тождественно
равен нулю и не сходится к функции
и ясно, что полученный ряд тождественно
равен нулю и не сходится к функции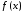 .
.
Получим разложение некоторых элементарных функций в степенные ряды.
Показательная
функция
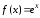 ,
,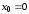 .
.
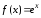 ,
,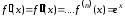 .
.
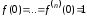 .
.
При
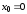 ряд Тейлора имеет вид:
ряд Тейлора имеет вид:
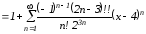
На
произвольном интервале
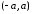
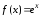 и все ее производные ограничены в
совокупности
и все ее производные ограничены в
совокупности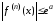 для
для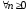 и
и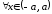 .
Тогда по следствию ряд сходится к
.
Тогда по следствию ряд сходится к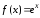 на
на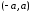 .
Так как число
.
Так как число произвольное, то ряд сходится на всей
числовой прямой.
произвольное, то ряд сходится на всей
числовой прямой.
Функция
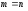 ,
,
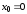 .
.
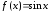 –бесконечно число
раздифференцируемая.
–бесконечно число
раздифференцируемая.
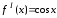 ,
,
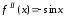 ,
,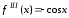 ,
,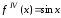 ,
…
,
…
Получаем
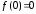 ,
,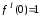 ,
,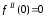 ,
,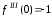 ,
,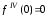 ,
…
,
…
Все ее производные
ограничены в совокупности на всей
числовой прямой
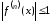 так как
так как
 .
.
Следовательно, формула
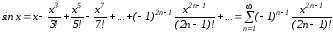
справедлива
при всех
 ,
т.е. степенной ряд сходится для
,
т.е. степенной ряд сходится для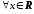 .
.
Функция
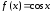 ,
,
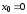 .
.
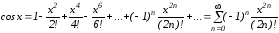
вывод аналогичный. Областью сходимости являетсяснова вся числовая прямая.
Степенная
функция
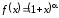 ,
, ,
,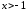 ,
,
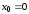 .
.
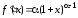 ,
,
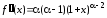 ,
,
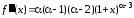 .
.
…
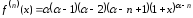 .
.
Вычисляя
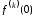 ,
получим степенной ряд Маклорена, который
называетсябиномиальным
рядом:
,
получим степенной ряд Маклорена, который
называетсябиномиальным
рядом:
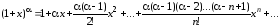
По
признаку Даламбера легко показать, что
областью сходимости биномиального ряда
является интервал
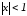 .
Поведение при
.
Поведение при зависит от
зависит от .
Показано, что
.
Показано, что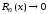 при
при .
.
Если
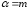 – натуральное число, то все коэффициенты
при степенях
– натуральное число, то все коэффициенты
при степенях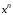 при
при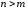 равны нулю и разложение превращается
в формулу бинома Ньютона, верную при
всех
равны нулю и разложение превращается
в формулу бинома Ньютона, верную при
всех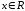
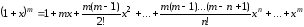 .
.
Стандартным
путем разложения известной функции в
степенной ряд является следующий:
вычисляют производные, формально
составляют ряд Тейлора и смотрят,
сходится или не сходится ряд к
 .
Однако часто этот путь является сложным.
Поэтому используют другие приемы, так,
например, были получены разложение
.
Однако часто этот путь является сложным.
Поэтому используют другие приемы, так,
например, были получены разложение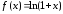 и
и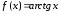 с помощью дифференцирования и
интегрирования известного степенного
ряда.
с помощью дифференцирования и
интегрирования известного степенного
ряда.
Логарифмическая
функция
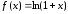
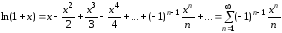 .
.
Интервал
сходимости
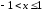 .
Это легко показать по признаку Даламбера.
.
Это легко показать по признаку Даламбера.
Функция
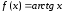 .
.
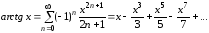
Интервал
сходимости
 .
.
Для разложений функций в степенные ряды обычно используют эти разложения, а также разложения
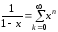 ,
,
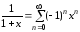 ,
справедливые при
,
справедливые при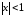 .
.
Пример
17.
Разложить в ряд
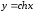 по
степенямх.
по
степенямх.
Решение.
Так как
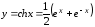 ,
то можно воспользоваться разложением
в ряд для функции
,
то можно воспользоваться разложением
в ряд для функции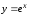 .
.
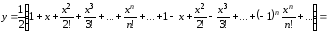

Пример
18. Разложить
в ряд
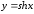 по степенямх.
по степенямх.
Решение.
Так как
 ,
то можно воспользоваться разложением
в ряд для функции
,
то можно воспользоваться разложением
в ряд для функции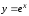 .
.
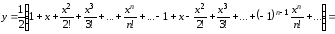

Пример
19.
Разложить в ряд
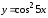 по степенямх.
по степенямх.
Решение. Воспользуемся формулой понижения степени и представим исходную функцию следующим образом
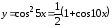 .
.
Воспользуемся
известным разложением в ряд функции
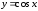 ,
получим
,
получим
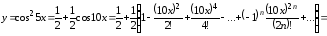
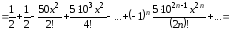
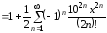 .
.
Пример
20.
Разложить в ряд
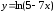 по степеням
по степеням .
.
Решение.
Преобразуем выражение для функции и
воспользуемся известным разложением
для
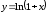 .
.
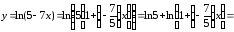
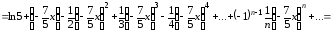
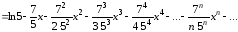
Пример
21.
Разложить в ряд
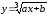 по степеням
по степеням .
.
Решение. Представим исходную функцию следующим образом
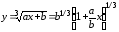 .
.
Вычислим коэффициенты ряда:
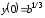 ,
,
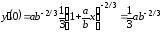 ,
,
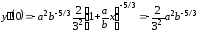 ,
,
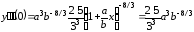 ,
,
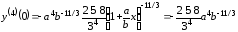 ,
…
,
…
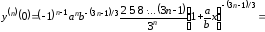
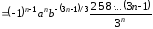 .
.
Получаем ряд
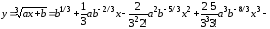
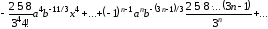
Пример
22.
Разложить в ряд функцию
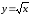 по степеням
по степеням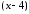 .
Указание
.
Указание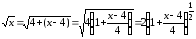 .
.
Решение.
Воспользуемся
формулой (9). Учитывая, что
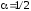 ,
получаем
,
получаем
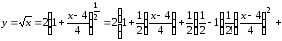
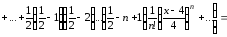
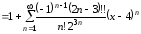 .
.
Замечание. Разложение функции в степенные ряды используют для решения многих задач: вычисления пределов; нахождения интегралов; приближенное вычисление значений функции; приближенного вычисления определенных интегралов; приближенного решения дифференциальных уравнений и т.д.
Пример 23. Вчислить интеграл с точностью δ=0,001: