17) Размещения и сочетания с повторениями – определение, формулы для расчета числа вариантов.

Размещениями с повторениями (или упорядоченными выборками с возвращениями) из n элементов по k называются упорядоченные наборы из k элементов множества M, в которых элементы множества могут повторяться.

8. Пусть дано множество M={1,2,3,4,5}. Тогда размещениями с повторениями из 5 элементов по 2 будут (1,1), (1,2), (2,1), (2,2), …,(5,1) и т.п. – любые упорядоченные пары из 2 элементов множества М.

Количество всех размещений с повторениями обозначим =Â(n,k). Поскольку в таком наборе из k элементов на каждом из k мест может стоять любой из n элементов исходного множества, число размещений с повторениями равно nn…n = n^k.  .

В отличие от выборок без повторений, количество выбираемых объектов может быть больше, чем количество типов, т.е. может быть k  n. Если вернуться к примеру 2.12 (а), то можно рассматривать и 10-разрядные числа.

1. (о мощности множества P(M) )

Для конечного множества M |2^M| = 2^|M|.

Доказательство:

Пусть конечное множество M состоит из n элементов, M = {x₁, …, x_n}. Сопоставим каждому его подмножеству двоичный вектор длины n. Если x_i входит в подмножество, то на i-м месте в этом векторе будет стоять 1, иначе – 0. Поскольку каждая компонента вектора может принимать только значения 0 или 1, а всего таких компонент n, то число различных векторов составит 2ⁿ. 

Следствие:

Можно сгенерировать все подмножества конечного множества M, перечислив некоторым способом все наборы из нулей и единиц длины n.

Можно выполнять такую генерацию различными способами (например, все наборы с одной «1», все с двумя «1», …). Это можно сделать наиболее эффективно, используя т.н. бинарный код Грея. Алгоритм построения бинарного кода Грея позволяет генерировать последовательность всех подмножеств n-элементного множества таким образом, что каждое последующее подмножество получается из предыдущего добавлением или удалением единственного элемента. Подробно этот алгоритм рассматривается при выполнении лабораторной работы.

Определим отношение эквивалентности на множестве размещений с повторениями из n элементов по k: (a₁,a₂,…,a_k) ~ (b₁,b₂,…,b_k)   cM число элементов a_i = c совпадает с числом элементов b_j = c.

Тогда сочетанием с повторениями из n элементов по k или неупорядоченной выборкой с возвращениями из n элементов по k является множество, которое состоит из элементов, выбранных k раз из множества M, причем один и тот же элемент допускается выбирать повторно.

9. В примере с множеством M={1,2,3,4,5} сочетания с повторениями из 5 элементов по 2 будут отличаться от размещений тем, что одинаковые по составу наборы будут независимо от порядка элементов в них считаться эквивалентными: (1,1), (1,2)~(2,1), (2,2), (5,2) и т.п.

При рассмотрении выборок с повторениями число n более наглядно трактуется как количество имеющихся в наличии типов объектов, а k – количество непосредственно выбираемых объектов. Раз объекты выбираются с повторениями, неважно, каково их реальное количество для каждого из типов. Можно считать их неисчерпаемыми.

Число всех сочетаний с повторениями обозначается =Ĉ(n,k) и вычисляется по формуле: Ĉ(n,k)= (2.2)

10. Пусть в кондитерской продается 10 различных видов пирожных. (n=10 – число типов). Сколькими способами можно купить 12 пирожных? (k=12). Ĉ(10,12)=C(10+12–1,12)=C(21,12)=21!/(12! (10–1)!)= 21!/(12! 9!).

18) Биномиальные коэффициенты. Теорема о свойствах биномиальных коэффициентов. Треугольник Паскаля.

Число сочетаний C(n,k)=– число различных k-элементных подмножеств n-элементного множества – встречается в формулах решения многих комбинаторных задач. Например, для определения числа подмножеств n-элементного множества, удовлетворяющих некоторому условию, задача разбивается на составные части: рассматриваются отдельно 1-элементные подмножества, 2-элементные и т.д., затем результаты складываются.

Числа =называютсябиномиальными коэффициентами.

• Свойства биномиальных коэффициентов

2. Число обладает следующими свойствами:

1. ; 2. ; 3.

Доказательство. 1. ==

2. ===== ===.

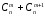3. = ====.

• Треугольник Паскаля

Из второй формулы теоремы 2.4 следует удобный способ рекуррентного вычисления значений биномиальных коэффициентов, который можно представить в графической форме, известной как треугольник Паскаля.

В этом равнобедренном треугольнике каждое число (кроме боковых единиц) является суммой двух стоящих над ним чисел. Тогда число сочетаний C(n,k) находится в (n+1) ряду на (k+1) месте. C(5,2)							1							0
						1		1						1
					1		2		1					2
				1		3		3		1				3
			1		4		6		4		1			4
		1		5		10		10		5		1		5
	…		…		…		…		…		…		…

19) Бином Ньютона и следствия.

3. (Бином Ньютона) При любых x, y  R (x+y)ⁿ = .

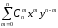Доказательство: По индукции.

База: n =1: (x+y)¹ = x+y = 1x¹y⁰+1x⁰y¹=x¹y⁰+ x⁰y¹= .

Индукционный переход: (x+y)ⁿ=(x+y)^n–1(x+y) = x+ y=x¹y^n–1+x²y^n–2+ …+x^n–1y¹+xⁿy⁰+x⁰yⁿ +x¹y^n–1+x²y^n–2 + …+x^n–1y¹= (+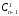)·x¹y^n–1+ (+)·x²y^n–2+…+(+)·x^n–1y¹+ (xⁿy⁰+ )·x⁰yⁿ = |=;=| =x¹y^n–1+x²y^n–2 +…+x^n–1y¹+xⁿy⁰+ x⁰yⁿ = .

Следствие 1. 2ⁿ = . Действительно, 2ⁿ = (1+1)ⁿ = .

Следствие 2. . Действительно, 0= (–1+1)ⁿ = .

1. ; 2.(Тождество Коши).

Доказательство:

1. 0·+1·+2·+…+(n–1)·+n·=(0+n)·+(1+n–1)·+ (2+n–2)·+…=n/2·.

2. – это число способов выбратьk предметов из m+n предметов. Их можно выбирать в два приема: сначала выбрать i предметов из первых n предметов, а затем недостающие k–i предметов – из оставшихся m предметов. Отсюда общее число способов выбрать k предметов составляет .