42) Булевы функции и булева алгебра. Аксиомы булевой алгебры. Их применение.

Функцией алгебры логики (ФАЛ) от n переменных x₁, x₂, …, x_n называется функция f:{0,1}ⁿ{0,1}, т.е. функция, которая произвольному набору (₁, …, _n) нулей и единиц ставит в соответствие значение f(₁, …, _n){0,1}.

ФАЛ называются также булевыми функциями, двоичными функциями или переключательными функциями. Аргументы булевой функции являются булевыми переменными. Булеву функцию можно задать таблицей истинности.

Утверждение Для булевой функции от n аргументов существует 2ⁿ различных наборов аргументов.

Булева функция f(x₁, x₂, …, x_n) называется полностью определенной, если ее значения определены на всех 2ⁿ наборах переменных. В противном случае функция частично определенная.

Функция существенно зависит от переменной x_i, (или переменная x_i – существенная), если  такой набор значений x₁, x₂, …, x_n , что. В противном случае переменнаяx_i – несущественная (фиктивная).

1. x1	x2	f1	f2
   0	0	0	1
   0	1	0	1
   1	0	1	0
   1	1	1	0

   Пусть две булевы функции заданы таблицей истинности. Для них переменная x₁ существенная, а x₂ – несущественная.

По определению булевы функции равны, если одна из другой получается введением или удалением несущественных переменных.

Одна и та же функция может иметь множество реализаций формулами над данным базисом (т.е. множеством логических операций). Формулы, реализующие одну и ту же функцию, называются равносильными (т.е. на всех наборах переменных их значение истинности совпадает). Отношение равносильности формул является отношением эквивалентности.

Пусть даны формулы F(y₁, y₂, …, y_m ), f₁(x₁, x₂, …, x_n ), …, f_m(x₁, x₂, …, x_n ). Тогда подстановкой формул f_i в формулу F называется следующая конструкция: (F| y_i f_i )(x₁, x₂, …, x_n)  F(f₁(x₁, x₂, …, x_n ), …, f_m(x₁, x₂, …, x_n )).

2. (О подстановке формул)

Если F(y₁, y₂, …, y_m ) и f_i (x₁, x₂, …, x_n ) – формулы алгебры логики, то (F| y_i f_i )(x₁, x₂, …, x_n ) также является формулой.

Иначе: Вместо некоторой подформулы в формулу может быть подставлена другая формула, и в результате получится правильно построенная формула.

Правило подстановки

Если в равносильных формулах: F(y₁, y₂, …, y_m ) G(y₁, …, y_m ) – вместо всех вхождений некоторой переменной y_i подставить одну и ту же формулу, то получатся равносильные формулы.

Правило замены

Если в формуле F заменить некоторую подформулу y_i на равносильную g_i, то получатся равносильные формулы.

ФАЛ, при образовании которых используются только операции отрицания, конъюнкции и дизъюнкции, называются булевыми формулами.

3. Для любой формулы алгебры логики существует равносильная ей булева формула.

2. Булевы функции и булева алгебра

Множество булевых функций с определенными на нем операциями отрицания, конъюнкции и дизъюнкции называется булевой алгеброй. Множество булевых функций от n аргументов будем обозначать P_n.

Для булевой алгебры выполняется ряд равносильностей, которые являются ее аксиомами.

Аксиомы булевой алгебры:

1. Операции с константами: 1) A  1  1; A & 1  A; 2) A  0  A; A & 0  0.

2. Противоречие: A & A  0.

3. Исключение третьего: A  A  1.

4. Идемпотентность: A & A  A; A  A  A.

5. Двойное отрицание:  A  A.

6. Коммутативность: A & B  B & A; A  B  B  A.

7. Ассоциативность: (AB)C  A(BC); (A&B)&C  A&(B&C).

8. Дистрибутивность: A & (B  C)  (A & B)  (A & C); A  (B & C)  (A  B) & (A  C).

9. Законы де Моргана: (A&B)  A  B; (AB)  A & B.

Используя приведенные аксиомы, возможно выполнять равносильные преобразования, выводить и доказывать новые законы. В частности, при выполнении преобразований часто используются законы поглощения: 1) A & (A  B)  A; A  A & B  A; 2) A & (A  B)  A & B; A  A & B  A  B.

Эти законы несложно доказать с помощью аксиом.

3. Принцип двойственности

Пусть f(x₁, x₂, …, x_n ) – булева функция. Двойственной к ней называется функция f^*(x₁, x₂, …, x_n )  f (x₁,x₂, …,x_n ). Из определения видно, что двойственность инволютивна: f^**=f.

Если двойственная функция f* совпадает с исходной функцией f, то такая функция f называется самодвойственной.

2. (0)* 01; (x)*= ¬(x)  x  Функция, тождественно равная своему аргументу, является самодвойственной.

4. (Общий принцип двойственности)

Если G(x₁, …, x_n ) получена подстановкой f_i из F(y₁, …, y_m ): G(x₁, …, x_n ) (F| y_i f_i )(x₁, …, x_n ), то G*(x₁, …, x_n ) (F*| y_i f*_i )(x₁, …, x_n ).

5. (Принцип двойственности для булевых функций)

Двойственная к булевой функции может быть получена заменой констант 0 на 1, 1 на 0, дизъюнкции на конъюнкцию, конъюнкции на дизъюнкцию и сохранением структуры формулы (т.е. соответствующего исходному порядка действий).

3. x	y	f=xy	x	y	f*
   0	0	0	1	1	1
   0	1	1	1	0	0
   1	0	1	0	1	0
   1	1	1	0	0	0

   (xy  z)*  (xy)  z., (xy)*  xy  в таблице истинности значения функции и переменных меняются на противоположные

4. Алгебра Жегалкина

Булевы функции с операциями умножения и сложения по модулю 2 образуют алгебру Жегалкина.

Аксиомы алгебры Жегалкина:

1. Операции с константами: A1  A; A0  0; A  0  A.

2. Идемпотентность: AA  A; A  A  0.

3. Коммутативность: AB  BA; A  B  B  A.

4. Ассоциативность: (A  B)  C  A (B  C); (AB)C  A(BC).

5. Дистрибутивность: A(B  C)  AB  AC.

Можно перейти от алгебры Буля к алгебре Жегалкина, используя следующие соотношения: A  1 A; AB=A  B  AB.

И наоборот, от алгебры Жегалкина к алгебре Буля: A  B =AB AB

4. Перейти к выражению булевой алгебры: (x  1)y (x  1) = xy x = xyx  xxy = (x y)x  0 =xy.

43) Нормальные формы. Теорема о разложении булевой функции по k переменным.

Табличный способ определения истинности сложного выражения имеет ограниченное применение, т.к. с увеличением числа логических переменных число вариантов становится слишком большим. Тогда может быть использован способ приведения формул к нормальной форме.

Аналитическое выражение функции (или формула) находится в нормальной форме, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, а знаки отрицания находятся только при переменных.

Элементарной дизъюнкцией (произведением) называется дизъюнкция (произведение) переменных или их отрицаний, в котором каждая переменная встречается только один раз.

ДНФ – это дизъюнкция элементарных произведений. КНФ – это произведение элементарных дизъюнкций. Как ДНФ, так и КНФ функции не единственна. Обычно предполагают, что входящие в ДНФ (КНФ) элементарные конъюнкции (дизъюнкции) попарно различны.

ДНФ (КНФ) называется совершенной, если каждая переменная формулы входит в каждую элементарную конъюнкцию (дизъюнкцию) ровно один раз.

• СДНФ (СКНФ) функции единственна.

5. Элементарные дизъюнкции: xy, z. Элемент. конъюнкции: xyz, x. f(x,y,z) = xyz xy – ДНФ ; f(x,y,z) = (x y)z – КНФ.

Введем обозначения:

6. О разложении булевой функции по k переменным (знак  ).

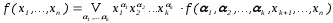
6. n=3, k=2.

Доказательство:

Выберем какой-либо набор значений для переменных x₁, …, x_n. Пусть это будет ₁, …, _n.. Заметим, что (1¹=1, 0⁰=1, 1⁰=¬1=0, 0¹=0)

Подставим в правую часть формулировки теоремы вместо x₁, …, x_n набор ₁, …, _n. Получим. Поскольку коэффициент перед функцией равен 1 только при равных значениях_i и _i, в разложении останется только один член: , и_i =_i, т.е. . Получена левая часть формулы теоремы 4.6. Поскольку набор был выбран произвольно, получаем, что утверждение верно набора x₁, …, x_n. ■

Следствие 1: Разложение Шеннона

Следствие 2: При k=n получаем: , т.е. выбираем те слагаемые, на которых функция равна 1. Полученная формула представляет собой СДНФ.

44) Совершенные нормальные формы и способы их построения.

Построение СДНФ

1. Построение по таблице истинности

1. Найти строки в ТИ, где f = 1.

2.  найденному набору ₁, …, _n. поставить в соответствие произведение , где

3. Составить дизъюнкцию из произведений п.2.

2. Получение из ДНФ.

Если некоторое произведение ДНФ не содержит какой-либо переменной (пусть x_k), то необходимо домножить это произведение на дизъюнкцию этой переменной и ее отрицания (т.е. на единицу, равную x_k x_k) и применить дистрибутивный закон.

Построение СКНФ

1. Построение по ТИ.

1. Найти строки в ТИ, где f = 0.

2.  найденному набору ₁, …, _n. поставить в соответствие дизъюнкцию , где

3. Составить произведение дизъюнкций из п.2.

2. Получение из КНФ.

Если некоторая элементарная дизъюнкция КНФ не содержит какой-либо переменной (пусть x_k), то необходимо дизъюнктивно добавить в нее произведение этой переменной и ее отрицания (т.е. x_kx_k) и применить дистрибутивный закон.

Произведения в СДНФ называются минтермами, а дизъюнкции в СКНФ – макстермами.

Может использоваться запись , которая означает, что в качестве минтермов берутся произведения, соответствующие двоичному представлению чисел. Аналогично, записьозначает, что в качестве макстермов берутся дизъюнкции, соответствующие двоичному представлению чисел.

45) Карты Карно: построение, определения, использование для нахождения упрощенного представления функции

Кроме аналитического, существуют геометрические способы представления булевых функций. Одним из таких способов является карта Карно.

Пусть дана булева функция f(x₁, x₂, …, x_n), определенная на 2ⁿ наборах переменных. Наборы, отличающиеся значением только одной переменной x_i, называются соседними.

Множество тех наборов, на которых f(x₁, x₂, …, x_n) = 1, называется прообразом единицы, множество наборов, на которых f(x₁, x₂, …, x_n) = 0 – соответственно прообразом нуля.

Карта Карно представляет собой таблицу прямоугольной формы, состоящую из 2ⁿ клеток. Каждая клетка соответствует одному из 2ⁿ наборов переменных. Любые две соседние клетки отличаются значением только одной переменной, т.е. представляют соседние наборы, причем считается, что противоположные концы каждой строки или столбца являются тоже соседними.

Булева функция может быть представлена на карте Карно выделением клеток, соответствующих прообразу 1. В этих клетках будем писать 1 и называть их p-клетками. Незаполненные ячейки соответствуют нулям функции. 2^k соседних p-клеток, расположенных в виде прямоугольника или квадрата, образуют k-мерный p-подкуб. Он называется покрытием размерности k и соответствует произведению n–k переменных. Одна p-клетка образует 0-мерный p-подкуб (или 0-куб), две – одномерный (1-куб, покрытие размерности 1 – произведение n–1 переменной – все кроме той, которая отличается для этих наборов), четыре – двумерный, и т.п.

Для функции трех переменных карту Карно можно представить в следующем виде:

Все клетки, отмеченные скобкой x_i (по строке и столбцу), представляют наборы с x_i = 1, а в неотмеченных строках и столбцах клетки соответствуют наборам с x_i = 0.

В случае четырех переменных карта Карно имеет следующий

46) Контактные схемы и булевы функции. Применение булевой алгебры для упрощения контактных схем.

Контактная цепь (схема) – устройство из проводов и контактов, связывающих два полюса. Любой контакт может быть либо замкнут, либо разомкнут. Контакты будем обозначать x₁, x₂, x₃, …

Контактной схеме будет соответствовать булева функция, которая принимает значение 1, если контур между двумя полюсами замкнут, и 0 – в противном случае. Основные операции булевой алгебры можно реализовать с помощью последовательного и параллельного соединения контактов.

Схема Булева операция

x₁x₂

x₁

Соответствие между схемой и булевой операцией легко проверить, сравнив работу схемы с таблицей истинности булевой функции. Для сложных контактных цепей можно построить более простую реализацию, упростив исходную булеву функцию с помощью аксиом булевой алгебры или применив один из методов минимизации булевой функции.

7. Пусть задана контактная схема. Упростить ее до пяти контактов. Составим булеву функцию для исходной схемы и упростим ее. . По упрощенной формуле составим схему: