
- •1.Логические исчисления 3
- •Логические исчисления
- •Логика высказываний
- •Понятие формальной теории
- •Исчисление высказываний (ив)
- •Теорема дедукции
- •Непротиворечивость и полнота исчисления высказываний
- •Методы проверки выводимости формул ив
- •X ├ (Xy)(Xz).
- •X, Xy├ Xz.
- •Понятие предиката
- •Логические эквивалентности с кванторами
- •Термы и формулы в исчислении предикатов
- •Аксиомы и правила вывода в исчислении предикатов
- •Теоремы об исчислении предикатов первого порядка
- •Метод резолюций для исчисления предикатов
- •Элементы теории алгоритмов и рекурсивных функций
- •Понятие алгоритма
- •Машина Тьюринга
- •X1 qi y1 ᅣ x2 qj y2
- •X1 qi y1ᅡx2 qj y2
- •Вычисление функций на машине Тьюринга
- •Алгоритмически неразрешимые задачи
- •Примитивно рекурсивные функции
- •Частично рекурсивные функции
- •Характеристики сложности алгоритмов
- •Классы сложности и
Частично рекурсивные функции
С помощью операций суперпозиции и примитивной рекурсии из простейших функций получаются только полностью определенные функции. Введем еще одну операцию – операцию минимизации функции.
Пусть имеется
арифметическая функция
![]() (возможно частично определенная). Пусть
существует какой-то механизм вычисления
этой функции, причем значение функции
не определено тогда и только тогда,
когда этот механизм работает бесконечно,
не выдавая никакого определенного
результата.
(возможно частично определенная). Пусть
существует какой-то механизм вычисления
этой функции, причем значение функции
не определено тогда и только тогда,
когда этот механизм работает бесконечно,
не выдавая никакого определенного
результата.
Фиксируем
произвольный набор значений
![]() для первых
для первых![]() аргументов функции
аргументов функции![]() и рассмотрим уравнение относительно
и рассмотрим уравнение относительно![]() :
:
![]() .
.
Чтобы
найти натуральное решение
![]() этого уравнения, будем вычислять при
помощи указанного выше "механизма"
последовательно значения
этого уравнения, будем вычислять при
помощи указанного выше "механизма"
последовательно значения
![]() для
для
![]() и сравнивать с
и сравнивать с![]() .
Наименьшее
значение
.
Наименьшее
значение
![]() ,
для которого получится
,
для которого получится
![]() ,
обозначим
,
обозначим
![]() .
Очевидно,
что
.
Очевидно,
что
![]() является
является![]() -арной
частичной функцией, которая полученаоперацией
минимизации
из функции
-арной
частичной функцией, которая полученаоперацией
минимизации
из функции ![]() .
.
Описанный
процесс нахождения
![]() будет продолжаться бесконечно в следующих
случаях:
будет продолжаться бесконечно в следующих
случаях:
Значение
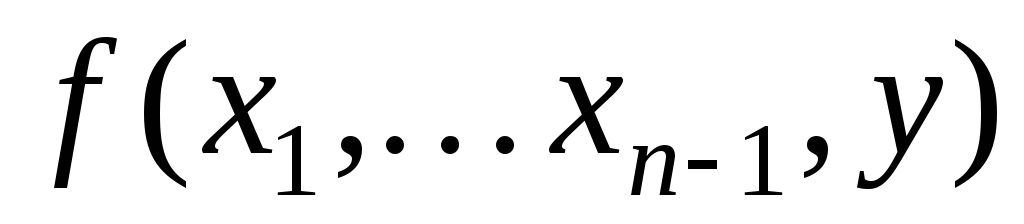 не определено для каждого
не определено для каждого

Значения
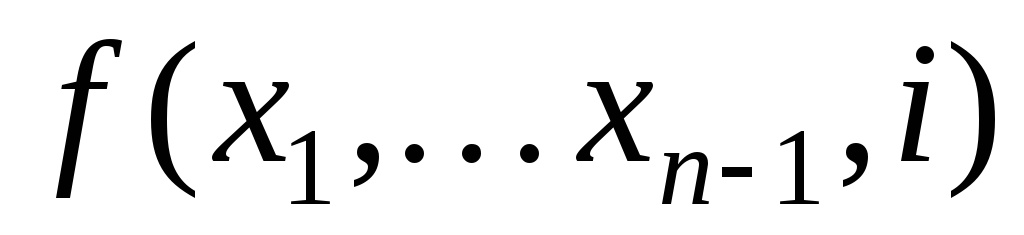 для
для
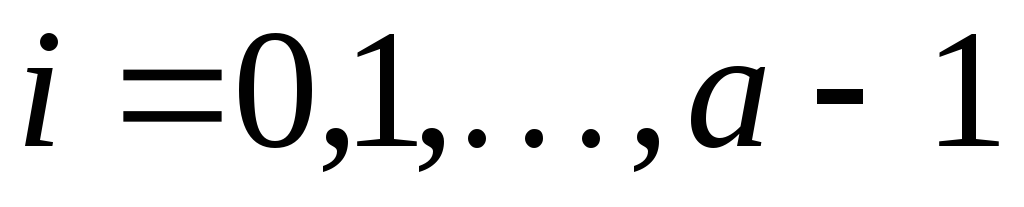 определены, но отличны от
определены, но отличны от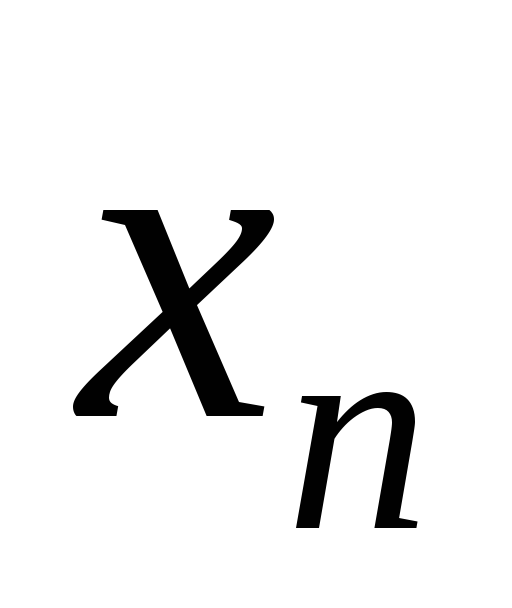 ,
а значение
,
а значение
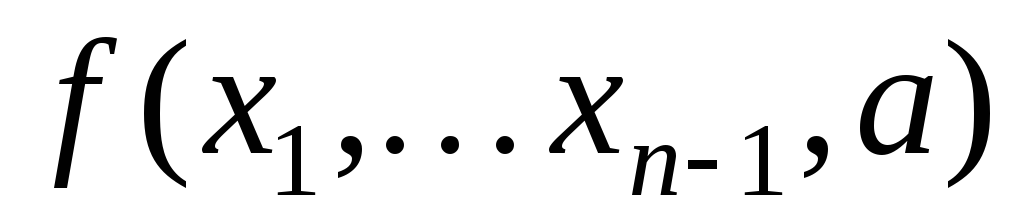 не определено.
не определено.Значения
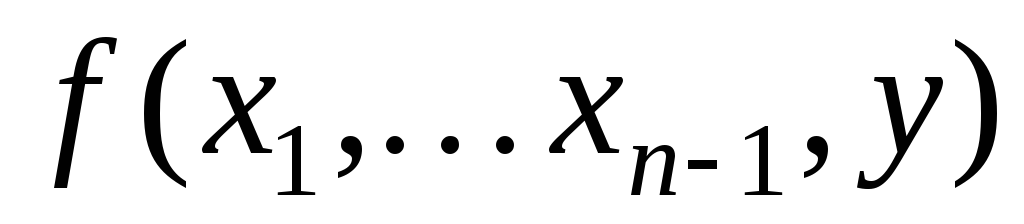 определены
для всех
определены
для всех
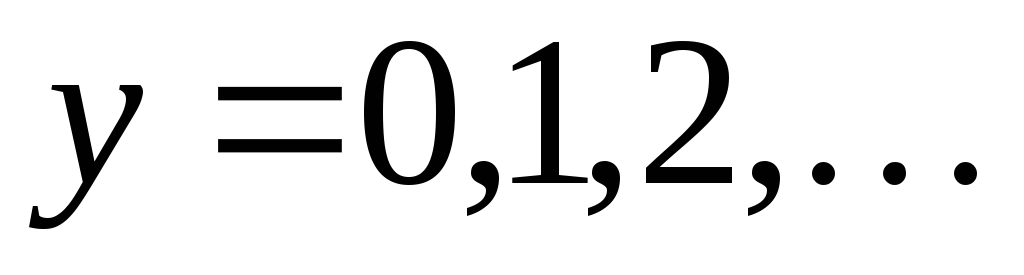 и отличны от
и отличны от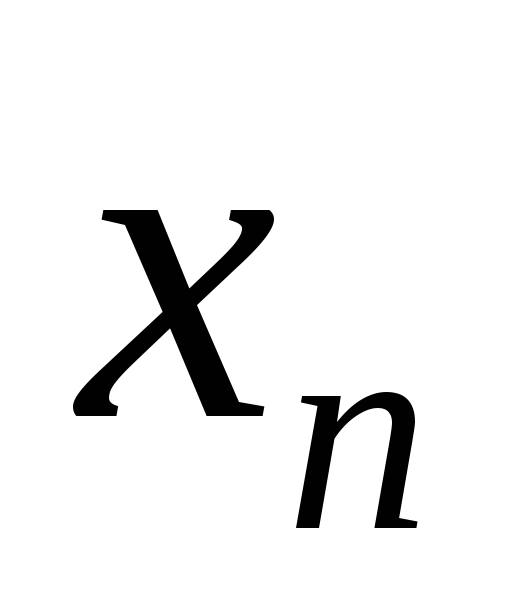 .
.
Во всех
этих случаях значение
![]() считается неопределенным. В остальных
случаях описанный процесс обрывается
и дает наименьшее решение
считается неопределенным. В остальных
случаях описанный процесс обрывается
и дает наименьшее решение![]() для уравнения
для уравнения
![]() .
.
Предложение (свойство операции минимизации).
Операция минимизации сохраняет интуитивную вычислимость функций.
Доказательство.
Пусть
необходимо вычислить значение функции
![]() на наборе
на наборе![]() для некоторой интуитивно вычислимой
функции
для некоторой интуитивно вычислимой
функции![]() .
Применим процедуру вычисления функции
.
Применим процедуру вычисления функции![]() на наборе
на наборе![]() .
Если через конечное число шагов процедура
определяет значение
.
Если через конечное число шагов процедура
определяет значение
![]() и
и
![]() ,
то полагаем значение функции
,
то полагаем значение функции
![]() равным0.
Если же
равным0.
Если же
![]() ,
то переходим к следующему этапу, на
котором применяем процедуру вычисления
функции
,
то переходим к следующему этапу, на
котором применяем процедуру вычисления
функции
![]() на наборе
на наборе![]() и т.д.
и т.д.
Если
на
![]() -ом
этапе вычислено значение функции
-ом
этапе вычислено значение функции
![]() и
и
![]() ,
то полагаем значение функции
,
то полагаем значение функции
![]() равным
равным![]() .
Если на
.
Если на
![]() -ом
этапе вычислено значение функции
-ом
этапе вычислено значение функции
![]() и
и
![]() ,
то переходим к следующему этапу и т.д.
,
то переходим к следующему этапу и т.д.
В
случаях, когда на каком-то этапе процедура
вычисления функции
![]() работает бесконечно или работа процедуры
завершилась безрезультатно, то считаем
функцию
работает бесконечно или работа процедуры
завершилась безрезультатно, то считаем
функцию
![]() неопределённой на наборе
неопределённой на наборе
![]() .
А так как описанная процедура пригодна
для любого набора
.
А так как описанная процедура пригодна
для любого набора![]() ,
то, очевидно, она представляет собой
алгоритм вычисления значений функции
,
то, очевидно, она представляет собой
алгоритм вычисления значений функции
![]() .
Предложение доказано.
.
Предложение доказано.
Процесс
вычисления
![]() ,
описанный выше, показывает, что если
функция
,
описанный выше, показывает, что если
функция
![]() интуитивно вычислима, то значение
интуитивно вычислима, то значение
![]() (если оно существует) может быть вычислено
эффективно.
(если оно существует) может быть вычислено
эффективно.
Частичная функция f называется частично рекурсивной, если она может быть получена из простейших функций конечным числом операций подстановки, примитивной рекурсии и минимизации.
Общерекурсивной функцией называется всюду определённая частично рекурсивная функция.
Далее рассмотрим примеры общерекурсивных функций.
Пример
1.
Простейшие функции
![]() ,
,![]() ,
,![]() для
для![]() всюду определены, поэтому они являются
общерекурсивными функциями.
всюду определены, поэтому они являются
общерекурсивными функциями.
Пример 2. Все примитивно рекурсивные функции являются общерекурсивными функциями.
Пример 3. Минимизируем примитивно рекурсивную функцию
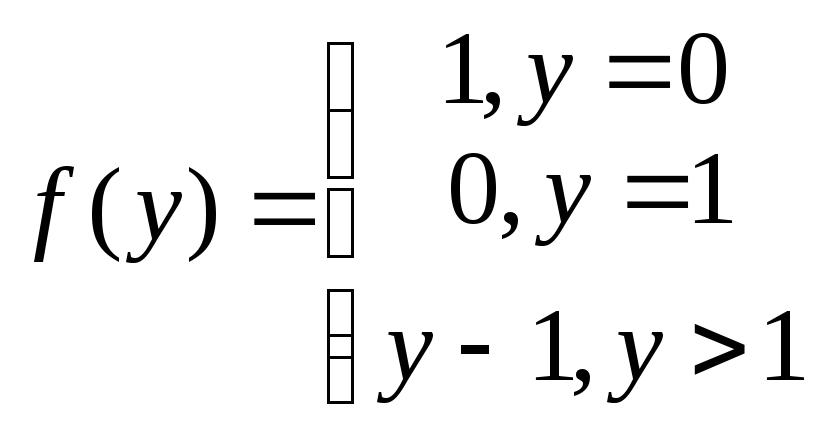
Составим
минимизирующее уравнение
![]()
Найдем
значения функции
![]() при различных значениях
при различных значениях![]() .
.
При
![]() нужно найти минимальное значение
нужно найти минимальное значение![]() ,
которое удовлетворяет условию
,
которое удовлетворяет условию![]() .
.
Полагаем
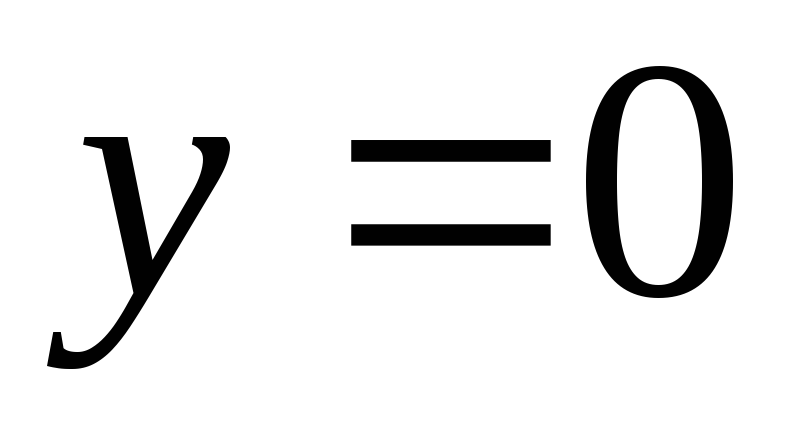 и находим значение
и находим значение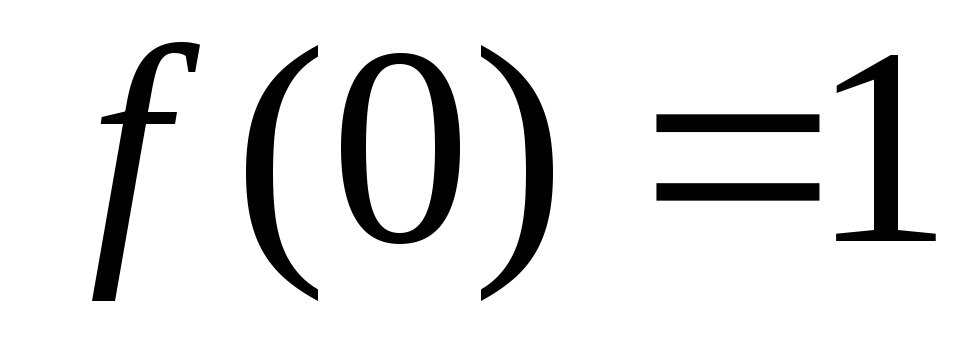 .
Оно не совпадает со значением
.
Оно не совпадает со значением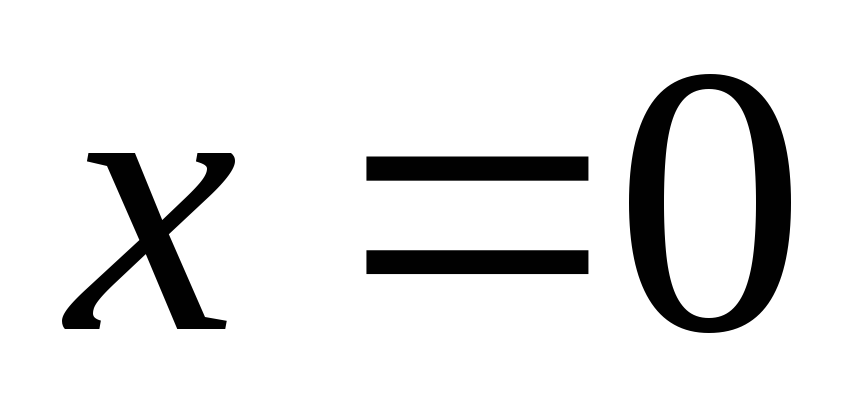 .
.Полагаем
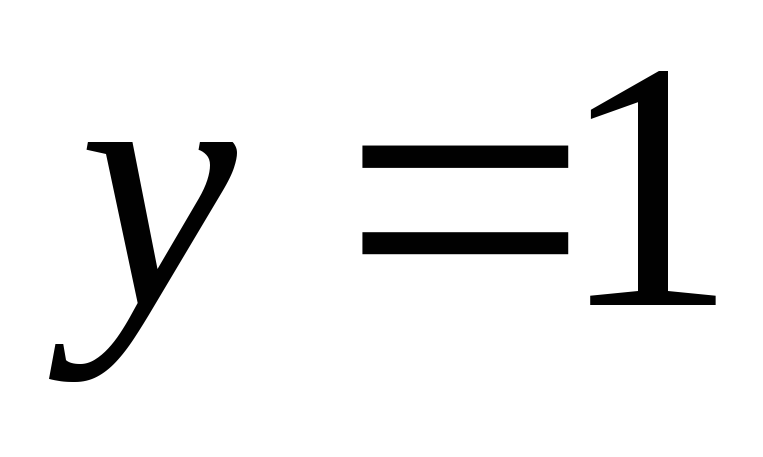 и находим значение
и находим значение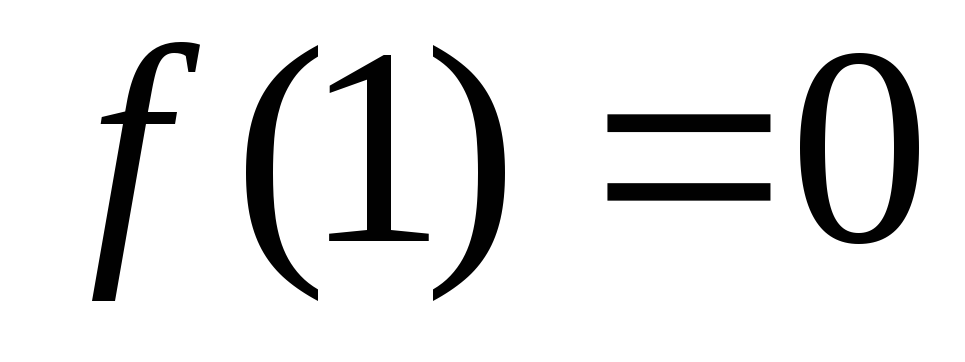 .Таким
образом, такое
.Таким
образом, такое существует и
существует и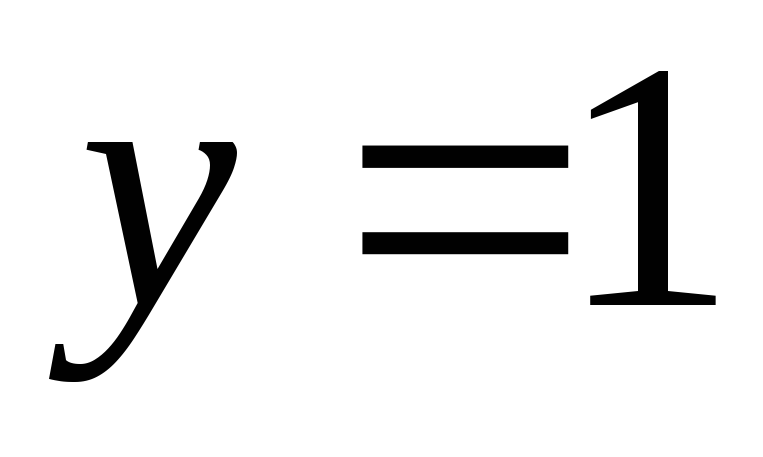 и
и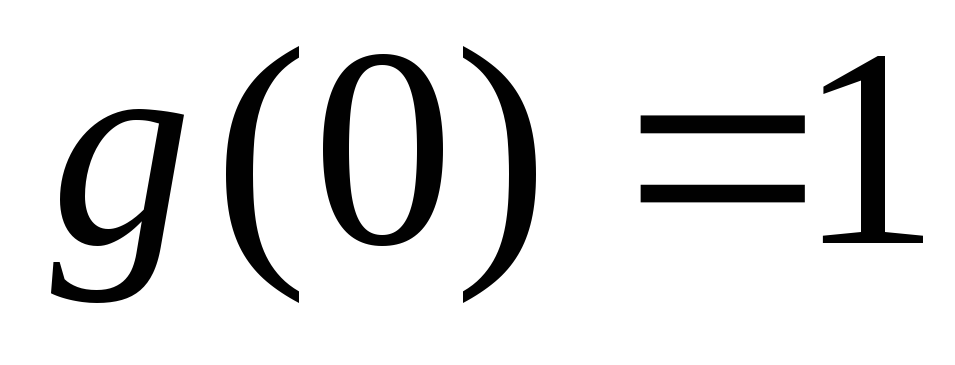 .
.
При
![]() нужно найти минимальное значение
нужно найти минимальное значение![]() ,
которое удовлетворяет условию
,
которое удовлетворяет условию![]() .
.
Полагаем
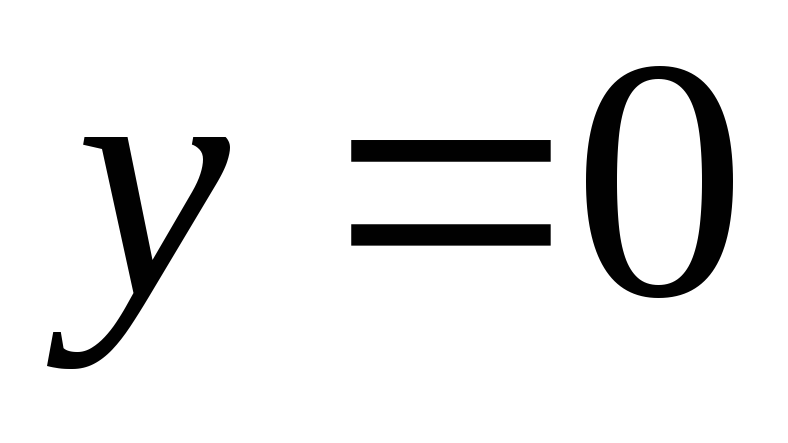 и находим значение
и находим значение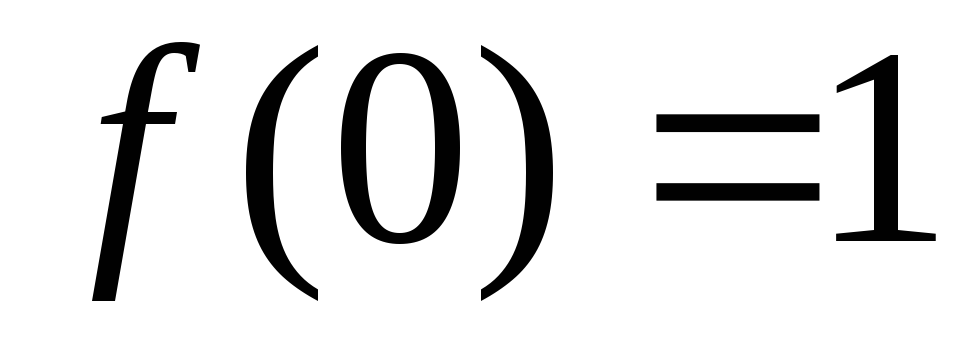 .Таким
образом, такое
.Таким
образом, такое существует и
существует и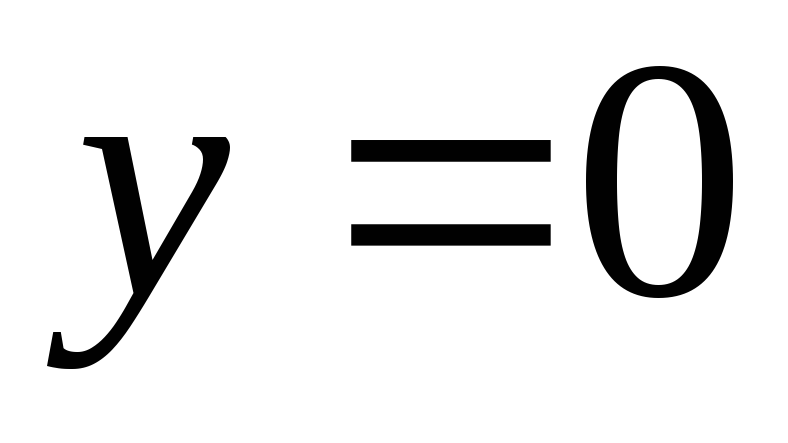 и
и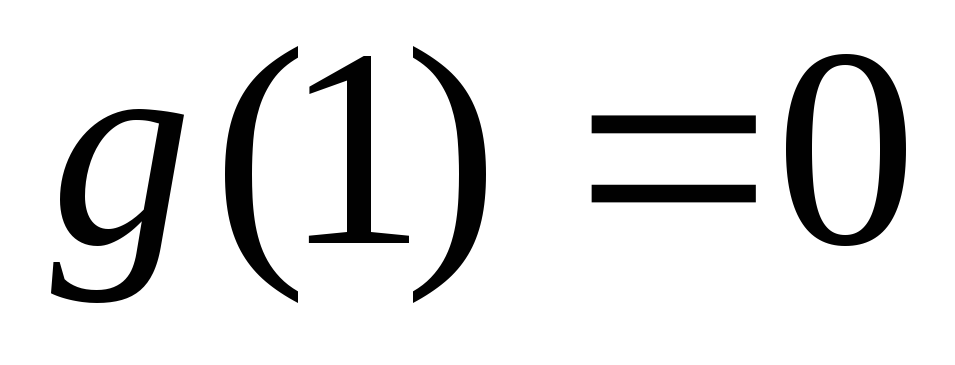 .
.
При
![]() нужно найти минимальное значение
нужно найти минимальное значение![]() ,
которое удовлетворяет условию
,
которое удовлетворяет условию![]() .
.
Полагаем
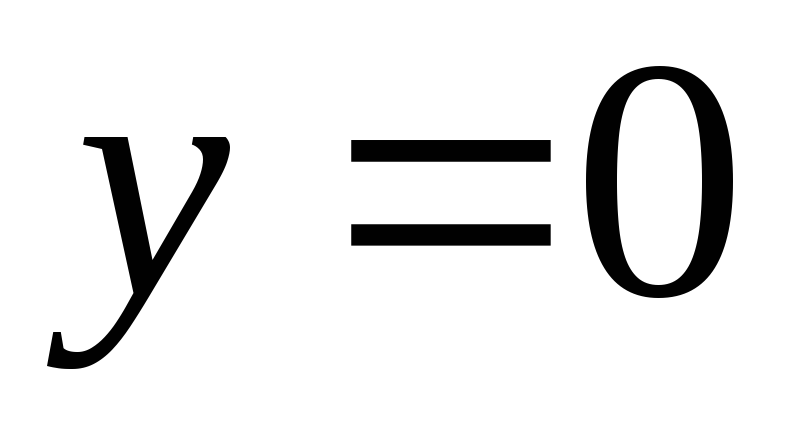 и находим значение
и находим значение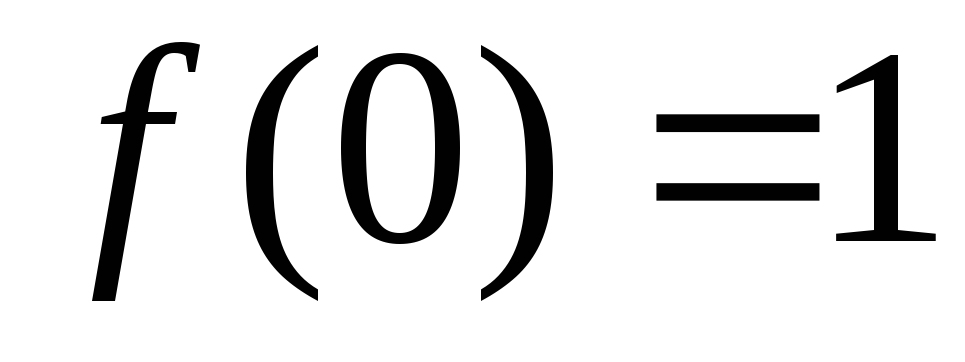 .
Оно не совпадает со значением
.
Оно не совпадает со значением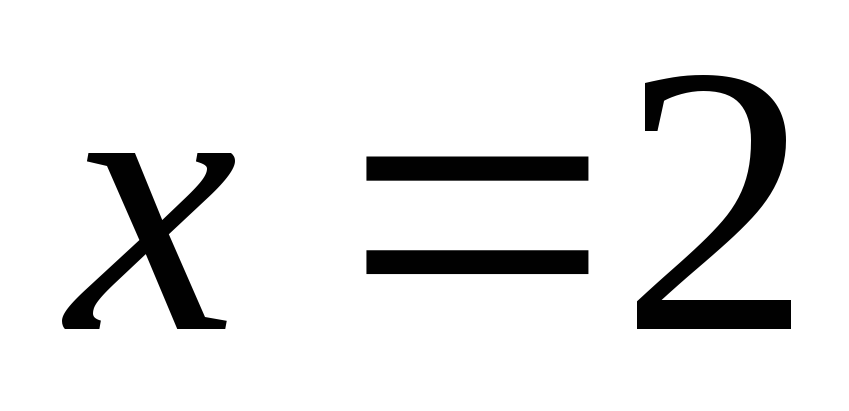 .
.Полагаем
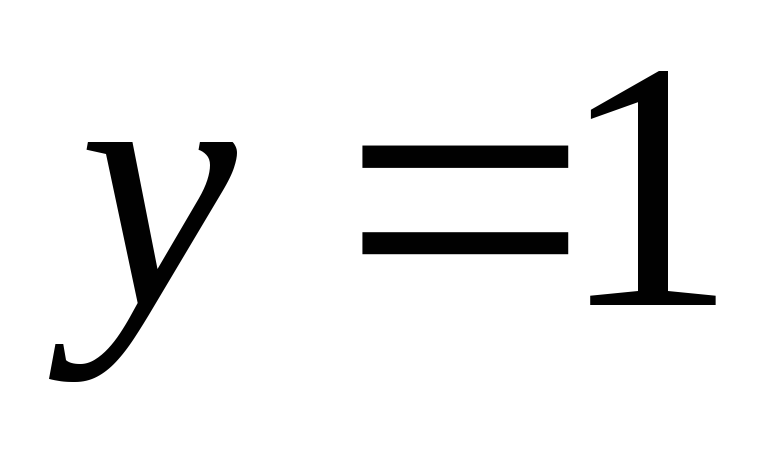 и находим значение
и находим значение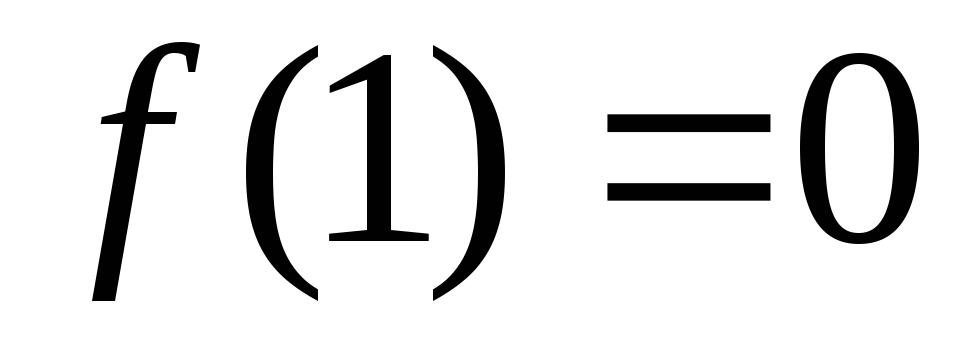 .
Оно не совпадает со значением
.
Оно не совпадает со значением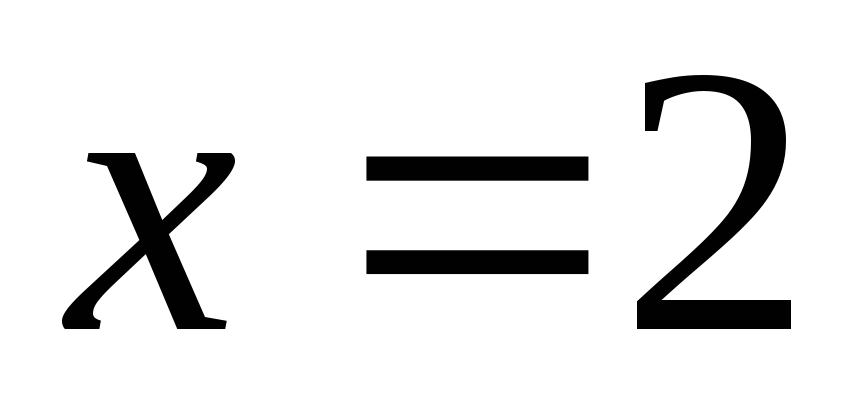 .
.Полагаем
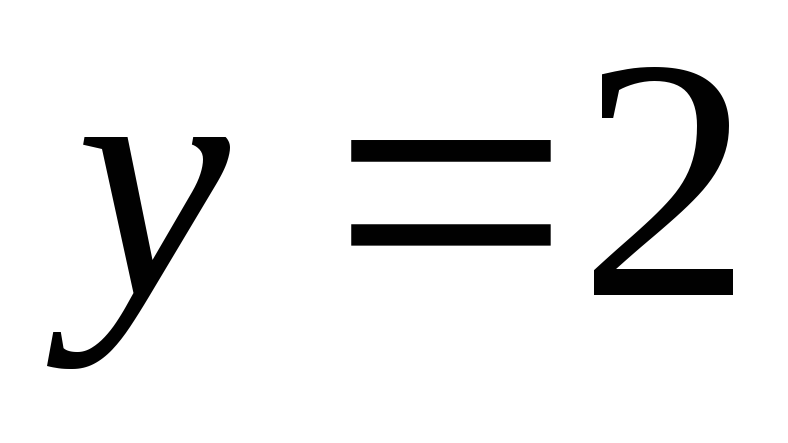 и находим значение
и находим значение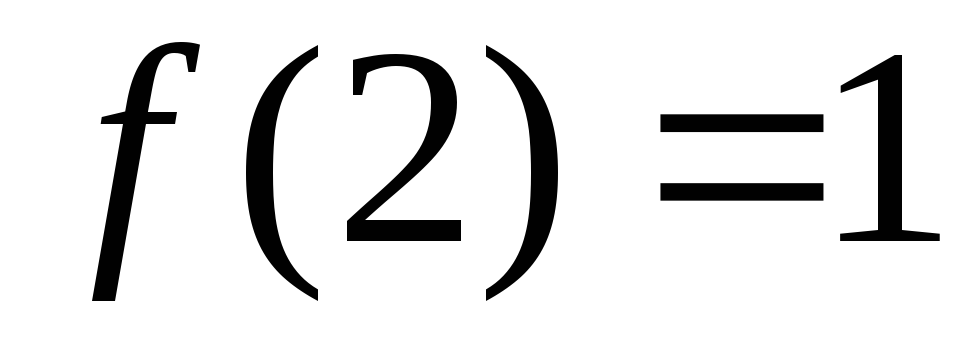 .
Оно не совпадает со значением
.
Оно не совпадает со значением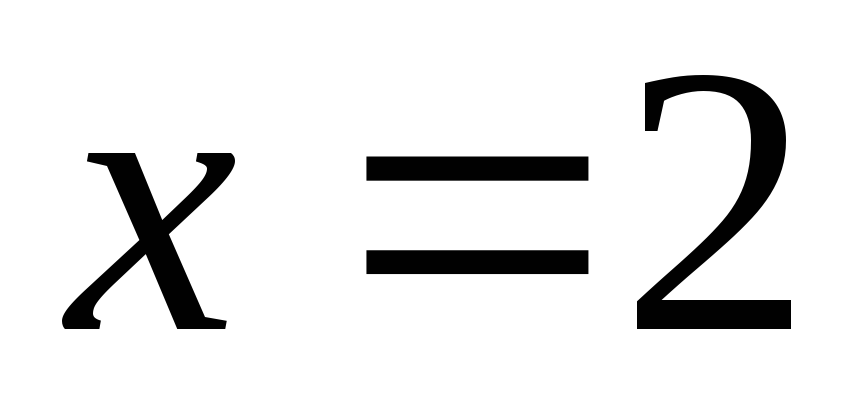 .
.Полагаем
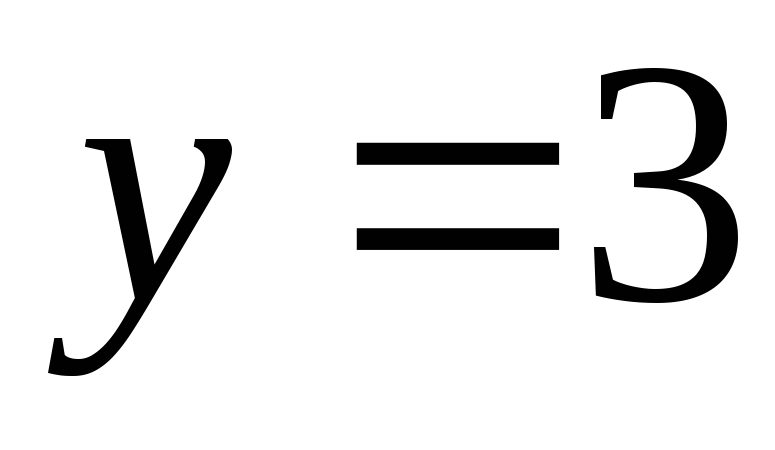 и находим значение
и находим значение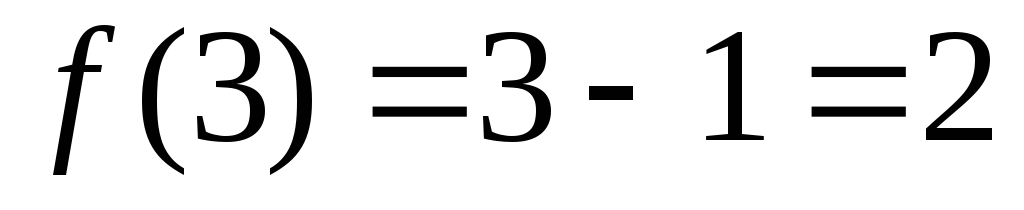 .
Таким образом, такое
.
Таким образом, такое существует и
существует и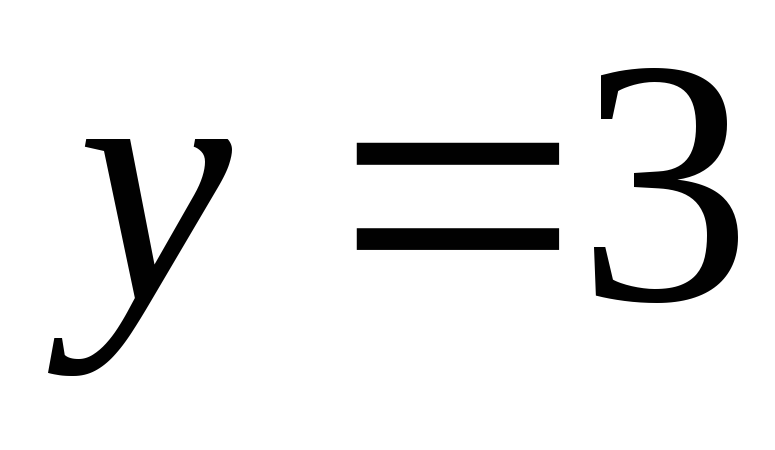 и
и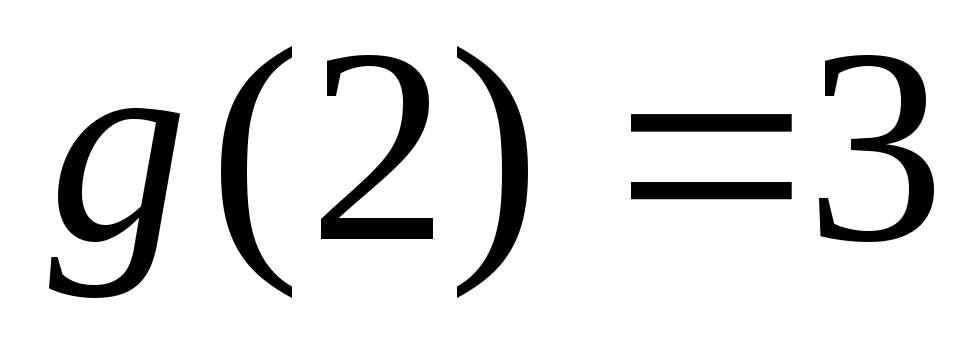 .
.
Для
остальных
![]()
![]() .
Получили, что функция
.
Получили, что функция![]() всюду определена и имеет следующий вид
всюду определена и имеет следующий вид
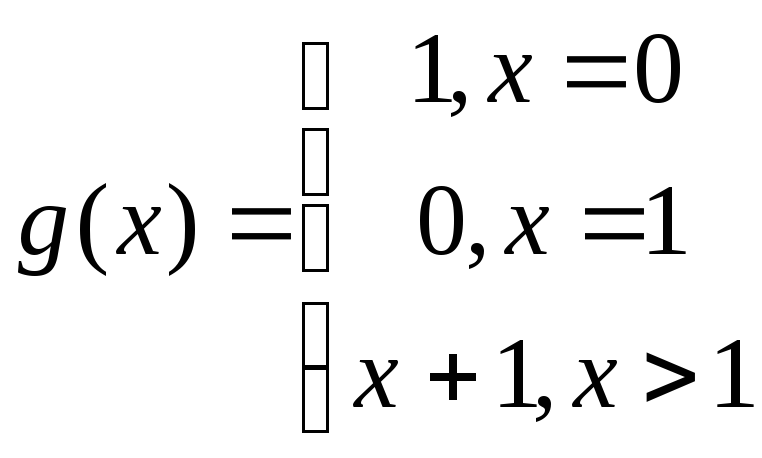
Далее рассмотрим примеры частично рекурсивных функций
Пример
1. Функция
![]() является частично рекурсивной, поскольку
может быть получена с помощью операции
минимизации из примитивно рекурсивной
функции сложения. Действительно,
является частично рекурсивной, поскольку
может быть получена с помощью операции
минимизации из примитивно рекурсивной
функции сложения. Действительно,![]() .
При
.
При![]() функция не определена.
функция не определена.
Пример 2. Рассмотрим функцию, заданную уравнением:
![]()
Результат операции минимизации не определен даже для точки х=0.
Действительно,
при
![]() нужно найти минимальное значение
нужно найти минимальное значение![]() ,
которое удовлетворяет условию
,
которое удовлетворяет условию![]() .
Очевидно, что среди неотрицательных
целых чисел такое
.
Очевидно, что среди неотрицательных
целых чисел такое![]() не существует. Таким образом, функция
не существует. Таким образом, функция![]() является частично рекурсивной функцией,
которая нигде
не определена.
является частично рекурсивной функцией,
которая нигде
не определена.
Пример 3. Рассмотрим функцию, заданную следующим образом
![]()
Найдем
значение
![]() .
При
.
При
![]() нужно найти минимальное значение
нужно найти минимальное значение![]() ,
которое удовлетворяет условию
,
которое удовлетворяет условию![]() .
Очевидно, что такое
.
Очевидно, что такое![]() существует и
существует и![]() .
Для
.
Для![]() результат
операции минимизации не определен,
поскольку подбор нужного значения
результат
операции минимизации не определен,
поскольку подбор нужного значения
![]() никогда не будет закончен.
никогда не будет закончен.
Пример
4. Минимизируем
функцию
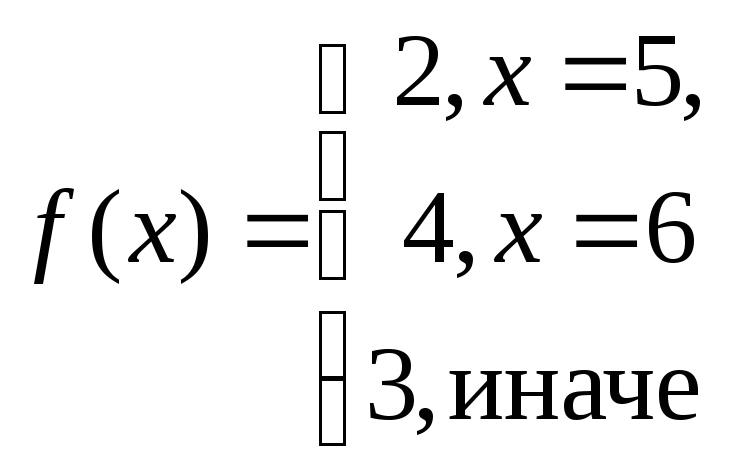 .
.
Уравнение, определяющее новую функцию выглядит так
![]()
Поскольку функция
![]() принимает только 3 значения (2,4,3), то
функция
принимает только 3 значения (2,4,3), то
функция![]() определена только при этих значениях,
в остальных точках значение функции
определена только при этих значениях,
в остальных точках значение функции![]() не определено. Найдем значение
не определено. Найдем значение![]() .Решая уравнение последовательной
подстановкой, находим, что первое
удовлетворяющее уравнению значение
равно 5, т.е.
.Решая уравнение последовательной
подстановкой, находим, что первое
удовлетворяющее уравнению значение
равно 5, т.е.![]() .
Аналогично определяем, что
.
Аналогично определяем, что![]() ,
,![]() .
Таким образом,
.
Таким образом,
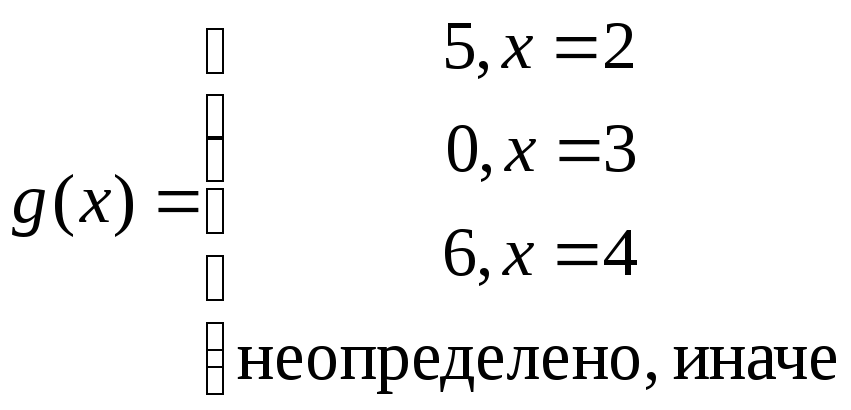
Обозначим KПРФ – множество всех примитивно рекурсивных функций, KЧРФ – множество всех частично рекурсивных функций, KОРФ – множество всех общерекурсивных функций, а KВФ – множество всех интуитивно вычислимых функций.
Связь между этими множествами функций показывает следующее.
Предложение (о иерархии классов рекурсивных функций)
KПРФÌКОРФÌКЧРФÌКВФ.
Доказательство. Первое включение следует из определений примитивной рекурсивности и общерекурсивности функций. Существуют примеры общерекурсивных, но не примитивно рекурсивных функций (примеры не приводятся из-за сложности и громоздкости), поэтому включение строгое.
Из определений частичной рекурсивности и общерекурсивности функций следует, что KОРФÌКЧРФ. Выше был приведен пример нигде не определённой частично рекурсивной функцией, а любая общерекурсивная функция является всюду определённой. Таким образом, имеет место строгое включение KОРФÌКЧРФ.
Очевидно, что KЧРФÌКВФ, т.е. любая частично рекурсивная функция интуитивно вычислима.
Сделаем два важных замечания:
в современной теории рекурсивных функций считают, что верно и обратное включение, т.е. любая вычислимая функция является частично рекурсивной (тезис Чёрча-Клини);
существуют функции, не являющиеся частично рекурсивными, а следовательно, если принять тезис Чёрча-Клини, то существуют функции, не являющиеся вычислимыми.
Предложение доказано.
