
64 лекции по математике кн2
.pdf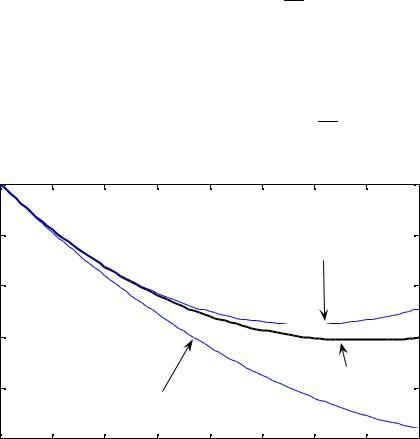
|
|
|
|
|
|
|
|
x |
|
|
|
Запишем уравнение в интегральной форме y(x) =1+ ∫(x − y)dx.Подставив |
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
под знаком интеграла |
вместо неизвестной функции y(x) |
начальное значе- |
|||||||||
ние |
y0 |
=1, получим первое приближение |
|
|
|
|
|
||||
|
|
|
|
|
x |
|
|
2 |
|
|
|
|
|
|
|
y1(x) =1+ ∫(x −1)dx =1− x + x |
. |
|
|
|
|||
|
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Второе приближение получаем, вычисляя интеграл |
|
|
|
|
|||||||
|
|
|
|
x |
|
|
|
|
3 |
|
|
|
|
|
y2 (x) =1+ ∫(x − y1(x))dx =1− x + x2 − x |
. |
|
|
|||||
|
|
|
|
0 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2=1-x+x2-x3/6 |
|
|||
|
|
0.8 |
|
|
|
|
|
|
|
|
|
|
|
0.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=2exp(-x)+x-1 |
|
||
|
|
0.6 |
|
|
y1=1-x+0.5x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
|
0.7 |
0.8 |
|
|
|
|
|
Рис. 42.1 |
|
|
|
|
|
|
На рис. 42.1 приведены графики точного решения y(x) = 2e− x + x −1и два полученных приближения. Существуют оценки погрешности метода Пикара, которые мы здесь рассматривать не будем. Важно знать, что они существуют.
Теперь перейдем к численным методам приближенного решения дифференциального уравнения первого порядка. Численно решить дифференциальное уравнение
y′ = f (x, y), y(x0 ) = y0
это значит, что для заданной последовательности аргументов |
x1,x2 |
,…,xn |
найти такие значения y1, y2 ,…, yn , что yk ≈ y(xk ), k =1,2,…,n, |
где |
y(x) |
искомое решение уравнения. |
|
|
22 |
|
|
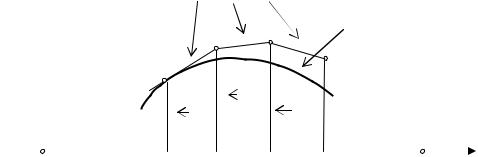
Рассмотрим один из самых простых численных методов – метод Эйлера. Идеи, положенные в его основу, являются исходными для ряда других, более точных методов. Пусть требуется найти решение уравнения на отрезке [x0,x0 + H ]. Разобьём отрезок на nравных частей и получим последовательность точек
xk = x0 + kh, k = 0,1,…, n −1, h = H /n .
В точке (x0 , y0 ) известно направление поля f (x0, y0 ), т.е. угловой коэффициент касательной к неизвестной интегральной кривой. Поэтому из
уравнения касательной в этой точке y − y0 = f (x0, y0 )(x − x0 ) |
мы можем |
||
получить приближённое значение ординаты y1 ≈ y(x1) |
искомой |
кривой |
|
(см. рис. 42.2) |
|
|
|
y1 = y0 + f (x0, y0 )(x1 − x0 ) = y0 + f (x0, y0 )h . |
|
|
|
В точке (x1, y1) нам опять известно направление поля |
f (x1, y1) |
и |
можно |
вычислить y2 ≈ y(x2 ) |
|
|
|
y2 = y1 + f (x1, y1)h. |
|
|
|
Таким образом, приближённо искомая интегральная кривая заменяется ломаной, и приближённые значения искомого решения вычисляются по формуле
yk = yk−1 + f (xk−1, yk−1)h.
Решение уравнения представляется в виде таблицы с шагом аргумента h
График прибл. реш.
Точное
реш.
|
y1 |
y0 |
y2 |
x0 x1 x2
Рис. 42.2
23
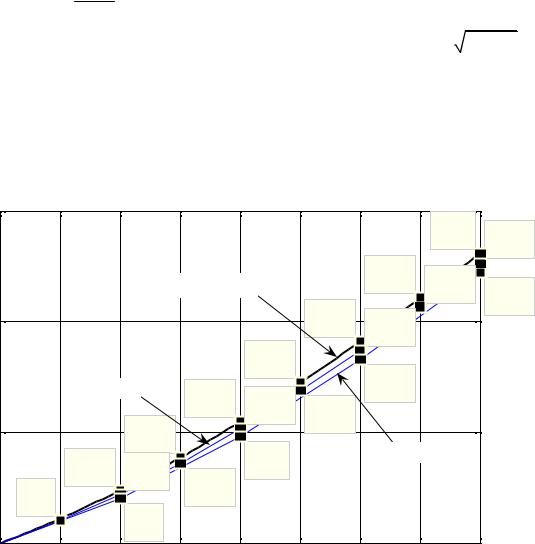
Пример. Методом Эйлера на отрезке [ 0;0,8 ] получить решение
уравнения y′ = y + x , y(0) =1. y − x
На рис. 42.3 приведен график точного решения y(x) = x + 
 2x2 +1, которое можно получить, решив уравнение как однородное (решите!), а также графики приближённых решений, вычисленные с шагом h = 0,2 (нижняя ломаная) и h = 0,1 (средняя кривая) соответственно. Для сравнения приведены также значения точного и приближённых решений в соответствующих точках.
2x2 +1, которое можно получить, решив уравнение как однородное (решите!), а также графики приближённых решений, вычисленные с шагом h = 0,2 (нижняя ломаная) и h = 0,1 (средняя кривая) соответственно. Для сравнения приведены также значения точного и приближённых решений в соответствующих точках.
2.5
|
|
|
X: 0.8 |
X: 0.8 |
|
|
|
Y: 2.31 |
|
|
|
|
Y: 2.269 |
|
|
|
|
|
|
|
|
X: 0.7 |
X: 0.7 |
|
y=x+sqrt(2x2+1) |
|
Y: 2.107 |
|
|
|
Y: 2.066 |
X: 0.8 |
||
|
X: 0.6 |
|
|
Y: 2.224 |
2 |
X: 0.6 |
|
|
|
Y: 1.911 |
|
|
||
|
Y: 1.872 |
|
|
|
|
|
|
|
|
|
|
|
|
X: 0.5 |
|
|
|
|
|
|
|
|
|
Y: 1.725 |
|
X: 0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h=0.1 |
X: 0.4 |
X: 0.4 |
|
Y: 1.828 |
|
|
|
|
|
|
|
Y: 1.549 |
X: 0.5 |
|
|
|
|
|
|
|
|
Y: 1.516 |
|
|
|
||
|
|
|
|
|
Y: 1.688 |
|
|
|
|
1.5 |
|
|
X: 0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Y: 1.386 |
|
|
|
|
|
|
|
|
|
|
|
|
|
h=0.2 |
|
||
|
|
X: 0.2 |
|
|
X: 0.4 |
|
|
||
|
|
X: 0.2 |
|
Y: 1.48 |
|
|
|
|
|
|
Y: 1.239 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
Y: 1.22 |
X: 0.3 |
|
|
|
|
|
||
|
X: 0.1 |
|
|
|
|
|
|
||
|
|
|
Y: 1.359 |
|
|
|
|
|
|
|
Y: 1.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X: 0.2 |
|
|
|
|
|
|
|
|
|
Y: 1.2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
0.1 |
|
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
Рис. 42.3
24

Лекция 43. Дифференциальные уравнения второго порядка
43.1. Задача Коши. Перейдем теперь к изучению дифференциального уравнения второго порядка. Общий вид этого уравнения следующий
F(x, y, y′, y′′) = 0. |
(43.1) |
Если из этого уравнения можно выразить старшую производную как функцию остальных переменных
y′′ = f (x, y, y′), |
(43.2) |
то такое его представление называют формой Коши.
Общее решение уравнения второго порядка содержит две произвольные постоянные. Например, уравнение y′′ = xлегко решается путем повторного интегрирования
y′ = x + C1 , y = x2 + C1x + C2 .
2
Для выделения частного решения требуется задать два условия. Один из возможных вариантов их задания представляет собой задачу Коши, состоящую в нахождении решения y(x), удовлетворяющего заданным на-
чальным условиям |
|
y(x0 ) = y0, y′(x0 ) = y1 . |
(43.3) |
Геометрически они означают, что интегральная кривая проходит через заданную точку (x0 , y0 ) и касательная к интегральной кривой в этой точке имеет заданный угловой коэффициент y1 . Условия существования и единственности решения задачи Коши формулируются в следующей теореме.
Теорема Коши. Пусть функции f (x, y, y′) , fy′(x, y, y′) и fy′′ (x, y, y′) непрерывны в некоторой окрестности точки (x0, y0 , y1) трехмерного пространства. Тогда существует и единственно решение уравнения (43.2), удовлетворяющее начальным условиям (43.3).
В отличие от дифференциального уравнения первого порядка, для которого при выполнении условий теоремы Коши интегральные кривые не пересекались на плоскости (x, y), для дифференциального уравнения второго порядка они, вообще говоря, пересекаются в этой плоскости. Однако, если рассмотреть кривые (x, y(x), y′(x)) в трехмерном пространстве (x, y, y′) , то согласно теореме Коши они не пересекаются.
25
43.2. Задача о цепной линии. Прежде, чем перейти к изложению некоторых методов решения дифференциальных уравнений второго порядка, рассмотрим задачу о так называемой цепной линии: какую форму принимает под действием силы тяжести однородная гибкая нерастяжимая тяжёлая нить с закреплёнными концами?
Эта задача возникла очень давно. Леонардо да Винчи (1452-1519) считал, что нить примет форму дуги окружности (если стрела прогиба нити невелика), а голландский математик Альбер Жирар (1595-1633) высказал предположение, что нить примет форму параболы. Получим дифференциальное уравнение, решением которого и будет функция, описывающая форму цепной линии. Выберем систему координат как на рис. 43.1.
y
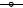 T
T
α
B 
H
A
o
x
Рис.43.1
Рассмотрим часть кривой AB так, что касательная в точке A горизонтальна. На неё действуют следующие силы: в точке A– горизонталь-
ное натяжение H , в точке B– направленное по касательной натяжение
T и вес части нити AB, пропорциональный её длине. Вес участка AB равен · , где p– вес единицы длины нити, а s– длина дуги AB. Согласно условиям равновесия сумма проекций вертикальных и горизонтальных составляющих всех сил должна быть равной нулю. Поэтому получаем
T cosα = H |
||||||
|
α = p |
. |
|
|||
T sin |
s |
|||||
Разделив второе равенство на первое, находим |
||||||
tgα = y′ = |
dy |
= |
p s |
. |
||
|
|
|||||
x |
|
dx |
|
H |
||
26 |
|
|
|
|
|
|

Наша задача свелась к решению этого дифференциального уравнения. Для того чтобы исключить переменную s, продифференцируем его по переменной x. В итоге получаем
y′′ |
= |
|
p |
|
d s |
. |
|
|
||
|
|
|
|
|
||||||
xx |
|
|
H d x |
|||||||
|
|
|
|
|
|
|
||||
Так как дифференциал дуги равен |
ds = 1+ y′2 dx, то получим диффе- |
|||||||||
ренциальное уравнение второго порядка |
||||||||||
|
p |
|
|
|
|
|||||
y′′ = |
|
|
1+ y′2 . |
|||||||
H |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Решим его, понизив порядок уравнения. Введем новую переменную z,
обозначив |
y′(x) = z(x) , и пусть, для краткости, |
p |
= |
|
1 |
. Тогда уравнение |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
a |
||||
примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dz |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
= |
|
|
|
1+ z2 . |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
dx |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
«Разделим» переменные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
dz |
= |
1 |
dx . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1+ z2 |
a |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Интегрируя, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
= |
x |
+ C . |
|
|
|
|||||||||||||||
|
|
|
ln |
z + |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1+ z2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
||
Из условия, что при x = 0 y′(0) = z(0) = 0 |
|
|
|
|
|
|
||||||||||||||||||||||||
(см. рис. 43.1), следует C = 0. |
||||||||||||||||||||||||||||||
Таким образом, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
z + |
1+ z2 |
= ex a . |
|
|
|
|
|
|
|
(43.4) |
|||||||||||||||||
Для того чтобы выразить |
z, умножим обе части этого равенства на |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
z − 1+ z2 |
и получим−1= (z − |
1+ z2 )ex a |
или |
z − |
1+ z = −e−x a . |
|||||||||||||||||||||||||
Сложив (43.4) с последним равенством, приходим к дифференциальному уравнению первого порядка
z = y′ = 12(ex a − e−x
a − e−x a ). Интегрируя, находим y = a2(ex
a ). Интегрируя, находим y = a2(ex a + e−x
a + e−x a )+ C1.
a )+ C1.
27
8 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
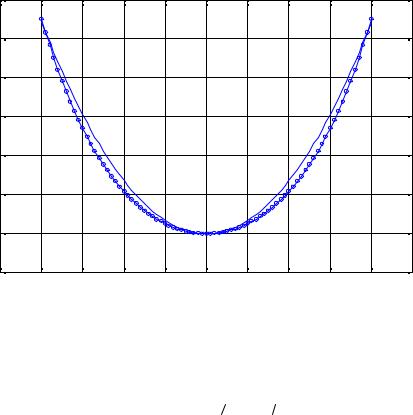
Рис. 43.2 |
|
|
|
|
Ясно, что любая кривая этого семейства имеет одну и ту же форму цепной линии
2 |
( |
|
) |
|
a |
||
y = |
a |
|
ex a + e−x a |
|
= ach |
x |
. |
|
|
|
|
||||
На рис. 43.2 эта кривая приведена для сравнения вместе с параболой. Таким образом, оказывается, что нить принимает форму гиперболиче-
ского косинуса. В оправдание выдающихся ученых, занимающихся этой задачей, стоит сказать, что в то время ещё не было показательной функции с основанием e ≈ 2,71828.... Задачу о провисающей верёвке решил в 1697г. оксфордский астроном и математик Д. Грегори (1661-1708).
43.3. Методы понижения порядка уравнения. Для решения задачи о цепной линии был использован метод, который применяется для дифференциальных уравнений второго порядка вида
y′′ = f (x, y′),
не содержащего явно переменной y.
Другой метод относится к уравнениям, не содержащим явно независимой переменной x, т.е.
y′′ = f (y, y′). |
(43.5) |
28 |
|
Введем новую функцию p = p(y) так, чтобы выполнялось y′(x) = p(y(x)). При этом предполагается, что y(x) ≠ const , так как в этом случае этот метод не применим (поэтому наличие таких решений нужно проверять отдельно). Найдем
y′′ = dp dy = dp p . dy dx dy
Тогда уравнение (43.5) сводится к уравнению первого порядка
dp p = f (y, p) dy
относительно неизвестной функции p = p(y) . Пусть p = p(y,C1)– его общее решение. Возвращаясь к исходной переменной, получим дифференциальное уравнение первого порядка
dy
dx = p(y,C1)
с разделяющимися переменными, решая которое, окончательно найдем общее решение уравнения (43.5)
∫ p(dyy,C1) = x + C2 .
Заметим, что решение получилось как зависимость x = x(y,C1,C2 ).
29
Лекция 44. Линейные дифференциальные уравнения второго порядка
Ранее мы рассмотрели несколько типов дифференциальных уравнений второго порядка, которые путем соответствующей замены переменной приводились к дифференциальным уравнениям первого порядка. Теперь мы перейдём к изучению важного класса линейных дифференциальных уравнений второго порядка, в которые неизвестная функция и ее производные входят линейно, т.е. имеющих вид
a0 (x)y′′ + a1(x)y′ + a2 (x)y = f (x) , |
(44.1) |
где функцииai (x), i =1,2,3 называют коэффициентами этого уравнения. Не умаляя общности, будем считать, что a0 (x) =1, т.к. к такому виду мож-
но привести уравнение (44.1) после деления на a0 (x) ≠ 0 . Если |
правая |
часть этого уравнения равна нулю |
|
y′′ + a1(x)y′ + a2 (x)y = 0, |
(44.2) |
то такое уравнение называется однородным, в противном случае оно называется неоднородным.
Будем предполагать, что функции a1(x), a2 (x) и f (x) непрерывны в интервале (a,b). Записав уравнение следующим образом
y′′ = −a1(x)y′ − a2 (x)y + f (x),
замечаем, что оно является частным случаем уравнения
y |
′′ |
′ |
|
|
′ |
− a2 (x)y + f (x). |
|
= F(x, y, y ) = −a1(x)y |
|
||||
Для существования и единственности решения задачи Коши требует- |
||||||
ся, чтобы функции F(x, y, y′) , F′(x, y, y′)и |
|
F′′ (x, y, y′) были непрерывны- |
||||
|
|
y |
|
|
|
y |
ми. В данном случае |
|
|
|
|
|
|
F′(x, y, y′) = −a |
(x), |
F′′ |
(x, y, y′) = −a (x) |
|||
|
y |
2 |
|
y |
|
1 |
и, следовательно, условия теоремы Коши выполнены. Поэтому при любых начальных условиях
y(x0 ) = y0, y′(x0 ) = y1, x0 (a,b) |
(44.3) |
уравнение (44.2) имеет единственное решение.
30
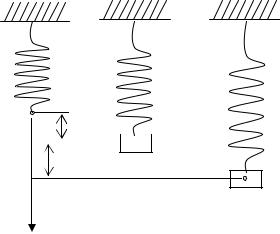
44.1. Линейный осциллятор. Уравнение вида (44.1) служит математической моделью разнообразных колебательных физических процессов. Например, рассмотрим движение груза массыm, подвешенного на пружине, массой которой пренебрегаем (см. рис. 44.1).
l
O
 x
x
Рис. 44.1
Предполагаем, что взаимодействие груза и пружины описывается законом Гука (сила пропорциональна удлинению). Вес грузаmg , вызвавший удлинение l пружины, уравновешивается силой упругости, т.е. k l = mg . Введём систему координат, приняв за начало точку O – положение равновесия груза на пружине. Выведем груз из положения равновесия и попытаемся определить его положение в любой момент времени, т.е. будем искать координату x как функцию времени x = x(t). Предположим также, что среда, в которой движется груз, оказывает сопротивление движению, пропорциональное (с коэффициентом пропорциональности h) скорости движения. Применяя второй закон Ньютона к движущейся массе, получим
mx = −hx − k( l + x) + mg , |
|
ɺɺ |
ɺ |
откуда следует уравнение вида (44.2)
mxɺɺ+ hxɺ + kx = 0.
Другой пример относится к электрическому контуру с конденсатором ёмкостиC, самоиндукцией Lи сопротивлениемR (см. рис. 44.2).Пусть q – заряд конденсатора и, следовательно, I = qɺ – сила тока в контуре. На обкладках конденсатора возникает напряжение q/C,в самоиндукции – ЭДС, равная−L dI /dt , а падение напряжения на сопротивлении равно−RI .
31
