
64 лекции по математике кн2
.pdf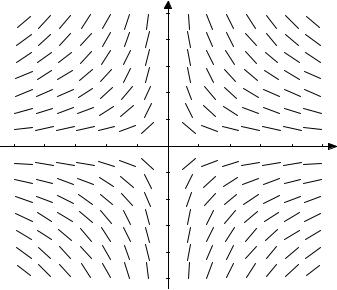
|
|
|
|
|
5 |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
||||||||||
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|
|
|
Рис. 40.4. |
|
|
|
|
|
Покажем, что если некоторая кривая y = y(x) проходит через точку (x0 , y0 )т.е. y0 = y(x0 )и касается направления поля в этой точке, то функция y = y(x) будет решением уравнения. Касание кривой заданного направления приводит к равенству векторов
{1, y′(x0 )} = λ{1, f (x0, y0 )}. Из этого равенства сначала следует, что λ =1, а потом
y′(x0 ) = f (x0, y0 ) = f (x0, y(x0 )).
Если это свойство (касание кривой заданного направления) происходит в каждой точке некоторого промежутка, т.е.
y′(x) = f (x, y(x)), a ≤ x ≤ b,
то последнее равенство и означает, что функция y = y(x)решение уравнения в указанном промежутке.
Эффективным способом построения поля направлений является так называемый метод изоклин. Изоклиной (кривой равного наклона) называется множество всех точек (x0 , y0 ), в которых угол наклона касательной один и тот же. Из (40.4) следует, что изоклина с данным коэффициентом k является кривой, которая задается уравнением
f (x, y) = k .
12
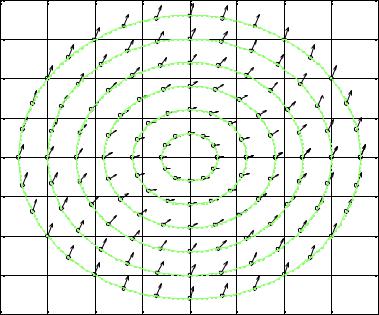
Построив эти кривые при некоторых значениях k |
и проводя на этих кри- |
|||||||
вых отрезки касательных под соответствующим углом, получим поле на- |
||||||||
правлений. Например, для уравнения |
|
|
|
|
|
|||
|
|
|
y′ = x2 + y2 |
|
|
|
||
изоклинами служат окружности x2 + y2 |
= k |
(см. рис. 40.5). |
|
|||||
2 |
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
-1.5 |
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
-2 |
-1.5 |
-1 |
-0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
Рис. 40.5.
Вообще говоря, нахождение решения дифференциального уравнения в виде формулы, связывающей независимую и зависимую переменные, представляет собой непростую задачу. Более того, для некоторых уравнений решение не может быть выражено через известные функции. Про такие уравнения говорят, что они не интегрируются в квадратурах. Странность термина объясняется тем, что вычисление интеграла исторически связано с вычислением площадей фигур (квадратурами). В этих случаях применяются разного рода численные методы, позволяющие на компьютере приближенно построить интегральные кривые. Однако, существуют классы дифференциальных уравнений, интегрируемых в квадратурах, т.е. для которых решение может быть найдено аналитически. Рассмотрим некоторые из них.
13

Лекция 41. Методы решений дифференциальных уравнений первого порядка
41.1. Уравнения с разделяющимися переменными. Если в дифференциальном уравнении
dy |
= f (x, y) |
(41.1) |
|
||
dx |
|
|
правая часть может быть представлена в виде произведения функций
f (x, y) = f1(x) f2 (y) ,
то такое уравнение называют уравнением с разделяющимися переменными. Решают его следующим образом. Произведём разделение переменных, записывая уравнение
|
dy |
= f (x) f |
|
(y) |
(41.2) |
||
|
|
|
|
||||
|
dx |
1 |
2 |
|
|
||
в виде |
|
|
|
|
|||
|
|
dy |
= f (x)dx, |
(41.3) |
|||
|
|
|
|
||||
|
|
f2(y) |
1 |
|
|
|
|
|
|
|
|
|
|
||
предполагая, что f2 (y) ≠ 0. Поскольку y – некоторая функция x, то, учитывая инвариантность формы первого дифференциала, получим
dy
∫ f2(y(x)) = ∫ f2 (y) = ∫ f1(x)dx .
Предположим, что последние два интеграла выражаются через элементарные функции в виде
F2 (y) = F1(x) + C .
Таким образом, мы получили общее решение уравнения (41.3). Сюда следует добавить также решения вида y = y , где f2 (y ) = 0, которые мы «потеряли» при делении уравнения (41.2) на функцию f2 (y).
41.2. Задача о форме вращающегося ножа. Начнем с примера. Пусть режущая кромка ножа – прямая. Оказывается, если нож пере-
мещается под прямым углом к своей режущей кромке, то разрезание происходит «хуже», чем в том случае, когда этот угол острый. Например, отрезая хлеб или другой продукт, мы, как правило, перемещаем нож под некоторым углом (см. рис. 41.1).
14
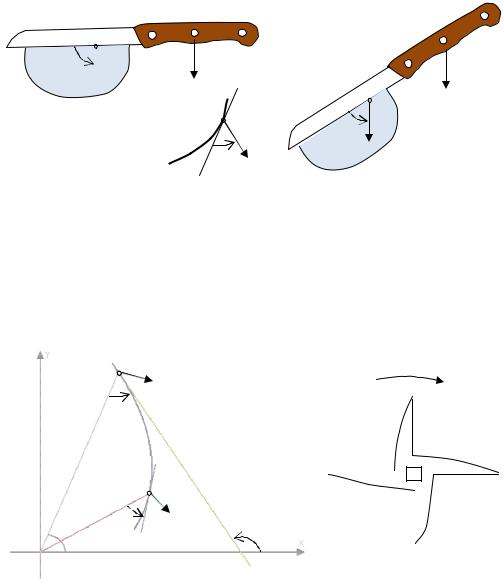
90° 
α
Рис. 41.1
Во многих инструментах режущая часть вращается, как например нож мясорубки. Если нож мясорубки имеет вид как на следующем рисунке, то он будет резать плохо, как отмечено выше.
,
α
|
|
|
|
|
|
|
|
φ |
α |
|
|
||
|
|
|
||||
|
|
|
||||
|
ψ |
|
|
|||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 41.2
Возникает вопрос: нельзя ли для вращающегося ножа отказаться от режущей кромки в виде прямой линии, но чтобы угол резания в каждой точке режущей кромки ножа был один и тот же. Ответ на этот вопрос важен с технической точки зрения для эффективной эксплуатации разного рода режущих инструментов.
Если режущая кромка ножа отлична от прямой линии, то под углом резания в данной точке будем понимать угол между касательной в этой точке к режущей кромке и направлением перемещения точки режущей кромки ножа (см. рис.41.1).
Итак, пусть нож, режущая кромка которого имеет форму некоторой кривой Г, вращается вокруг точки O . Поскольку угол резания в каждой точке один и тот же, то также будет постоянным и угол α = OMT между
15

радиус-вектором точки M (x, y) и касательной MT к этой кривой в точке M (x, y) (см.рис.2). В математической постановке задача формулируется
следующим образом: найти такую кривую |
|
y = f (x), чтобы в каждой её |
||||||||||||||||||||||||||||||
точке M (x, y) угол между касательной |
MT и радиус-вектором |
OM был |
||||||||||||||||||||||||||||||
постоянен и равен α . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для обозначенных на рисунке углов имеем |
|
|
|
|
ψ = α + ϕ, |
|
причём |
|||||||||||||||||||||||||
tgψ = y′, а |
tgϕ = y |
x |
. Используя формулу тангенса суммы |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg(α + ϕ) = |
|
tgα + tgϕ |
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1− tgαtgϕ |
|
|
|
|
|
|
|
|
|
|
|||||||||||
получаем дифференциальное уравнение первого порядка |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k + y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
y′ |
= |
|
|
|
|
x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1− k y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где обозначено k = tgα . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для его решения выполним |
подстановку |
y |
|
= t |
, т.е. от зависимой |
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||
переменной |
y перейдем к новой переменной t , являющейся функцией x . |
|||||||||||||||||||||||||||||||
Так как y = t x, то |
y′ = t+ x |
dt |
|
и приходим к уравнению с разделяющими- |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ся переменными |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t + x |
dt |
= |
k + t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
dx |
1− kt |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Разделяем переменные и интегрируем∫ |
1 |
− kt |
|
dt = k ∫ |
dx |
, |
|
|
|
|
||||||||||||||||||||||
1 |
+ t2 |
x |
|
|
||||||||||||||||||||||||||||
|
|
|
arctgt − |
k |
ln(1+ t2 ) = kln |
|
x |
|
− klnC . |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Возвращаясь к «старым» переменным, имеемarctg |
|
y |
|
= k ln |
|
x2 + y2 |
|
. |
||||||||||||||||||||||||
|
x |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|||
Полученную зависимость удобнее представить в полярной системе коор-
динат, что приводит к уравнению
ϕ
r = C e k .
16
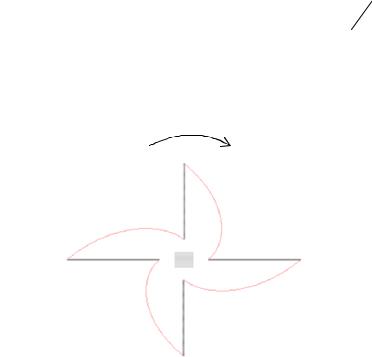
Это так называемая логарифмическая спираль. Она была известна многим математикам семнадцатого века, например, Декарту и Торричелли. Логарифмическая спираль часто встречается как в живой, так и неживой природе. Раковины улиток, а также рога некоторых животных закручены по логарифмической спирали. В подсолнухе семечки расположены по дугам, близким к логарифмическим спиралям.
Например, полагая 0,5 и k =1 при 0 ≤ ϕ ≤ π |
, мы получим |
2 |
|
часть дуги логарифмической спирали r = 0,5 eϕ ,по которой можно выто-
чить режущие кромки ножа для мясорубки с углом резания α = 450 (см. рис.41.3).
Рис.41.3
41.3. Однородные дифференциальные уравнения. Рассмотренная нами задача позволяет выделить ещё один тип дифференциального уравнения первого порядка, интегрируемого в квадратурах. Для его характеристики привлечём понятие однородной функции. Такая функция выделяется следующим свойством:
f (t x,t y) = f (x, y) , t,
т.е. при умножении её аргументов на одно и то же число значение функции не изменяется. Если в этом тождестве положить t =1/ x , то
|
y |
|
y |
|
f (x, y) = f (1, |
|
) = ϕ |
|
, |
|
|
|||
|
x |
x |
||
т.е. однородная функция может быть представлена как функция отношения своих аргументов.
17

Уравнение y′ = f (x, y), у которого правая часть однородная функция, называется однородным уравнением и сводится подстановкой
y = t(x) , y = t x , y′ = t + x dt
x |
|
|
|
|
|
|
dx |
||
к уравнению с разделяющимися переменными. Действительно, |
|||||||||
t + x |
dt |
= ϕ(t) или xdt = (ϕ(t) − t)dx |
|||||||
dx |
|||||||||
|
|
|
|
|
|
|
|
||
Предполагая, что ϕ(t) − t ≠ 0 |
и x ≠ 0, разделяем переменные и интегриру- |
||||||||
ем |
|
|
|
|
|
|
|
||
|
|
∫ |
dt |
= ln |
|
x |
|
+ C . |
|
|
|
|
|
||||||
|
|
ϕ(t) − t |
|||||||
|
|
|
|
|
|
|
|||
Обозначая интеграл слева через Φ(t) , получаем общее решение исходного уравнения в виде
Φ( y ) = ln x + C . x
К этому следует добавить решения, которые могут быть потеряны при делении на функцию ϕ(t) − t . Метод решения однородных уравнений открыл Иоганн Бернулли в 1695 году.
18

Лекция 42. Линейные дифференциальные уравнения. Приближенные методы решений дифференциальных уравнений первого порядка
42.1. Решение линейного уравнения и уравнения Бернулли. Линейным дифференциальным уравнением первого порядка называется уравнение вида
A(x)y′ + B(x)y + C(x) = 0
или, после деления на функцию A(x), вида
y′ + p(x)y + q(x) = 0,
в которые переменные y и y′ «входят» линейно. Покажем, что решение этого уравнения может быть найдено в виде произведения двух функций, т.е.
y = u(x)v(x),
каждая из них удовлетворяет уравнению с разделяющимися переменными. Подставляя y и производную y′ = u′v + uv′ в исходное уравнение,
его можно представить в одном из следующих видов:
′ |
′ |
+ pv) + q = 0 |
(42.1) |
u v + u(v |
|
или
(u′ + pu)v + uv′ + q = 0.
Рассмотрим, например, первое уравнение. Выберем функцию v такую, чтобы выражение в скобке обратилось в ноль, т.е. удовлетворяющую дифференциальному уравнению с разделяющимися переменными относительно неизвестной функции v(x)
dv + p(x)v = 0 . dx
Пусть v = v (x) – одно из его решений (полученное, например, при постоянной интегрирования, равной нулю). При функции v = v (x) уравнение (42.1) примет вид дифференциального уравнения с разделяющимися переменными относительно неизвестной функции u(x)
du
dx v (x) = −q(x).
19

Находя его общее решение в виде u = u(x,C), получим общее решение исходного линейного дифференциального уравнения в виде
|
|
y = u(x,C)v (x). |
|||||
В качестве примера вернемся |
к уравнениюm |
dy |
= mg − ky ,которое |
||||
|
|||||||
|
|
|
|
|
|
dt |
|
описывает изменение скорости y(t) |
падающего тела. Приведем это урав- |
||||||
нение к виду |
|
|
|
|
|
|
|
|
|
y′ + ay = g , |
|||||
где для краткости |
a = k /m. Подстановка y = uv приводит сначала к урав- |
||||||
нениюv ′ + |
a v = |
0 ,решение которого v (t) = e−at . Далее получим урав- |
|||||
|
|
|
|
|
|
||
нениеu′ = |
geat ,откуда найдемu = |
|
g |
e a t + C .Наконец, получим общее |
|||
|
|
||||||
|
|
|
|
a |
|||
решение исходного уравнения |
|
|
|
|
|||
|
|
y (t ) = ( g a + C e − a t ) . |
|||||
Отметим, что так называемое уравнение Бернулли, имеющее вид |
|||||||
|
|
y′ + p(x)y + q(x)yα = 0, |
|||||
сводится к линейному уравнению следующим образом. Будем считать, что α ≠ 0 и α ≠1, т.к. оба эти случая соответствуют линейным уравнениям. Поделим обе части уравнения на yα
yyα′ + p(x)y1−α + q(x) = 0
и введем новую переменную z = y1−α . В новых переменных исходное уравнение будет линейным
1z′ + p(x)z + q(x) = 0.
1− α
42.2.Приближенные методы решения дифференциальных уравнений первого порядка. Теперь остановимся на приближенных методах. Сначала рассмотрим метод Пикара (метод последовательных приближений). Представим задачу Коши
20
y′ = f (x, y), y(x0 ) = y0
в следующем эквивалентном виде: найти функцию y(x) такую, что
x
y(x) = y0 + ∫ f (x, y(x))dx.
x0
Фактически, мы заменили дифференциальное уравнение интегральным уравнением, в котором неизвестная функция y(x) входит ещё и под знак интеграла. Если под знаком интеграла функцию y(x) заменить её значением y0 , получим так называемое первое приближение
x
y1(x) = y0 + ∫ f (x, y0 )dx .
x0
Затем заменяем y(x) найденной функцией y1(x) и получаем второе приближение
x
y2 (x) = y0 + ∫ f (x, y1(x))dx.
x0
Продолжая процесс далее, найдем
x
yn (x) = y0 + ∫ f (x, yn−1(x))dx .
x0
Таким образом, получаем последовательность функций
y1(x), y2 (x), …, yn (x),… |
(42.2) |
Оказывается, что при определенных условиях эта последовательность сходится к решению исходной задачи Коши. Под этим понимается, что для каждого x из рассматриваемого интервала числовая последовательность (42.2) имеет пределом соответствующее значение решения y(x). Справедлива следующая теорема, которую приведём без доказательства.
Теорема. Пусть в окрестности точки (x0 , y0 ) функция f (x, y) и ее
частная производная |
fy′(x, y) непрерывны. Тогда в некотором интервале, |
содержащем точку |
x0 , последовательность функций (42.2) сходится к |
функции y(x), являющейся решением задачи Коши для данного уравнения.
Пример. Решим этим методом следующую задачу
y′ = x − y, y(0) =1, y(x) =?
21
