64 лекции по математике кн2

получим формулу для вычисления длины дуги AB .

Рис. 54.3

Если отрезки, на которые делится кривая, достаточно малые, то длина li

отрезка кривой Ai−1Ai приблизительно равна длине хорды Ai−1Ai . По теореме Лагранжа приращение yi функции y = y(x) на участке (xi−1, xi ) равно значению производной в некоторой точке ξi

приращение xi , т.е. yi = y′(ξ i) xi . Таким образом, для плоского случая (рис.54.3) будем иметь

Li ≈ Ai−1Ai = xi2 + yi2 = 1+ y′2(ξi) xi

и, следовательно,

.

Нетрудно видеть, что под знаком предела стоит интегральная сумма для функции 1 на отрезке (a,b), и потому последний пре-

дел равен определенному интегралу от этой функции на этом отрезке. Таким образом,

b

L= ∫ dl = ∫ 1+ y′ 2(x)dx

AB a

102

Пусть теперь f (x, y)– произвольная непрерывная функция, определенная в точках близких к кривой AB . Так как, согласно определению, точка Pi

на отрезке кривой Ai−1Ai может выбираться произвольным образом, то вы-

ленному интегралу от этой функции на данном отрезке. В результате мы приходим к формуле

b

Пример. Найти массу части кривой y=2-x2соединяющей точки A(0,2) и B(1,1), если плотность распределения массы вдоль

кривой задана функцией ρ(x,y)=2x(рис.53.4).

Рис. 54.4

103

Плоский случай. Параметрическое задание кривой. Пусть кривая AB

определена параметрическими уравнениями

x= x(t); y= y(t); α≤t ≤β,

где x(t)и y(t)дифференцируемые функции, производные которых непре-

Для её вывода достаточно в формуле (54.7) осуществить замену перемен-

тах. Попробуем вывести формулу для вычисления криволинейного инте-

Вспомним, что связь между декартовыми и полярными координатами определяется формулами x=rcosϕ, y=rsinϕ. Если в них вместо r под-

ставить его выражение из уравнения (54.8), то получится параметрическое уравнение кривой AB :

в котором в качестве параметра выступает полярный угол ϕ, изменяющийся в пределах от ϕ1до ϕ2 . При этом

x′2 (ϕ)+ y′2 (ϕ) = (r′(ϕ)cosϕ − r(ϕ)sinϕ)2 + (r′ (ϕ)sinϕ + r(ϕ)cosϕ)2

= r2(ϕ)+ r′2(ϕ).

104

Подставляя это выражение в соотношение (54.7), получим формулу для вычисления криволинейных интегралов 1-го рода в случае, когда кривая АВ на плоскости задана в полярных координатах:

Пример. Найти массу половины кардиоиды r = (1+cosϕ), 0≤ ϕ≤ π,

если плотность ρ = r в каждой её точке.

Рис. 54.5

Пользуемся формулами (54.3) и (54.10):

π

M = ∫ ρdl = ∫r r2 (ϕ) + r′2 (ϕ)dϕ =

Общий пространственный случай. Если кривая AB расположена в пространстве, то, как правило, она задается параметрическими уравнениями

x = x(t); y = y(t); z = z(t) α≤t ≤β,

причем параметру t =α соответствует точка A, а параметру t =β соответ-

окружающей кривую AB, и, проводя рассуждения, подобные приведенным для плоского случая, придем к следующей формуле:

54.3. Некоторые приложения криволинейного интеграла 1-ого рода. Определение пло щади цилиндрической поверхности. На рис.54.6 изображено ограждение переменной высоты некоторой гор изонтально расположенной территори и, ограниченной кривойL. Вопрос о расходе краски, необходимой для окр аски этого ограждения, сведется к нахождению его площади. Если ввести систему координат так, чтобы территория находилась в плоскости XOY, то можно считать, что данное огра ждение представляет собой часть цил индрической поверхности с направл яющей L и образующей, параллельной оси OZ, причем высота ограждения задается функцией z = f (x, y), определенной в каждой точке кривой L(рис.54.6). Если

рассмотреть часть п оверхности на небольшом участке кривой Ai−1Ai , то можно считать, что высота этой части постоянна и равна значению

Рис. 54.6

Суммируя по всем уч асткам и переходя к пределу в поллучающейся интегральной сумме, мы придем к тому, что площадь всей б оковой поверхно-

сти ограждения будет определяться по формуле S = ∫ z(x, y)dl.

L

106

Вычисление массы, координат центра тяжести и моментов инерции материальной кривой. Часто математическую идеализацию пространственного материального объекта можно представить в виде пространственной кривойAB, вдоль которой распределена масса с линейной плотностью ρ(x, y,z) (рис.54.1). (Канаты, на которых подвешен мост через пролив Босфор, соединяющий Черное и Средиземные моря, можно рассматривать в качестве примера такого объекта. В качестве математической модели канатов можно рассматривать их осевые линии с постоянной линейной плотностью, равной массе тонкого слоя поперечного сечения). В таком случае основные механические характеристики подобных объектов могут быть вычислены с помощью криволинейного интеграла 1-ого рода.

а)Масса материальной кривой. Как мы уже знаем, масса М такой кривой может быть вычислена по формуле (54.3).

б) Моменты инерции Ix, I y, Izотносительно осей OX ,OY ,OZ . Перечисленные моменты вычисляются по следующим формулам

кие участки и считаем, что вся масса отрезка кривой (приблизительно рав-

C(xc, yc,zc ) материальной пространственной кривой могут быть высчитаны по формулам:

где M– масса кривой.

Пример. Найдем механические характеристики верхней полуок- ружности радиуса Rс центром в начале координат, вдоль которой равномерно распределена масса с плотностьюρ .В данном примере мы имеем дело с плоской кривой и потому в соответствующих формулах мы должны опустить переменную z. Очевидно, что масса M равна длине полуокружности, умноженной на ρ , т.е. M = πρR .

107

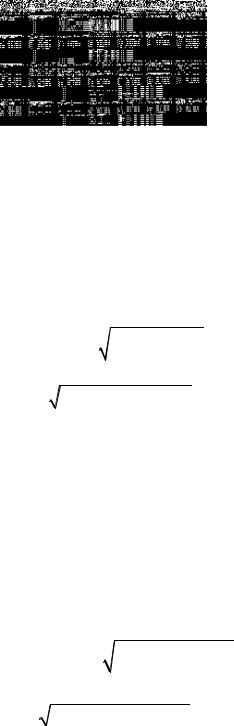
Рис.54.7

Для нахождения моментов инерции Ix и Iyсначала запишем уравнение полуокружности в пара метрическом виде

а затем воспользуемсся формулой (54.11) (для плоского случая) и (54.8). Будем иметь

Что касается координат центра тяжести C(xc, yc ), то в силу симметрии xc = 0, а для вычисления yc опять используем параметрическое уравнение полуокружности:

108

Лекция 55. Криволинейные интегралы 2-г о рода (по координатам)

В данной лекци и мы рассмотрим еще одну интегральную конструкцию, которая, как и все рассмотренные ранее, изначально возникла при стремлении решить н екоторую прикладную задачу (именно в физике), а потом оказалась при менимой при решении других теоретических и прикладных задач. Речь идет о криволинейных интегралах 2 -го рода.

55.1. Определение и обозначения. Физическая зад ача, в которой подобная конструкция возникает, формулируется следующ им образом. Пусть в некоторой области D пространства определено силовое поле, т.е. на материальную точку ед иничной массы, помещенную в область D, действует зависящая от ее местонахождения вектор-сила F. И пусть в этой области материальная точка перемещается по кривой L из положения A в положение B. Требуется о пределить работу W сил данного поля при таком перемещении.

Рис. 55.1

На рисунке 55. 1 изображено плоское поле сил. Ясно, что при перемещении точки по кр ивой L по участку кривой ACB силы поля оказывают положительное воздействие, т.е. совершают положительную работу, а при движении по участку кривой DEF они оказывают отрицательное воздействие, т.е. совершают отрицательную работу. Точно также при спуске с горы мы ощущаем положительное воздействие силы тяжести, а при подъеме в гору нам приходится преодолевать отрицательное воздействие этой силы.

Если в пространстве введена декартова система к оординат, то сила,

действующая в точке M(x,y,z) может задаваться посредс твом ее разложе-

ния по единичным ве кторам i, j,k

109

где функции P(x,y, z),Q(x,y,z), R(x,y,z)являются проекциями силы на оси

Рис. 55.2

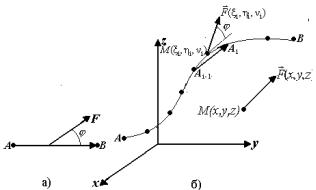
Ясно, что в случае к риволинейной траектории перемещ ения и непостоянной по величине и направлению силы, данная формула для подсчета работы неприменима. На помощь, как часто в подобных случаях, приходит интегральная методология. В согласии с ней, для решения поставленной задачи разобьем кривую Lна n отрезков (см. рис.55.2,б). Работа W сил

110

поля по кривой AB очевидно будет равна сумме работWi (i = 1,..., n) по этим отрезкам кривой. Если считать, что: а) сила поля на отрезке кривой

но как сумма произведений соответствующих координат этих векторов.

R(ξi ηi,νi), а координатами вектора Ai−1 Ai будут приращения координат при переходе от точки Ai−1к точке Ai т.е. числа xi, yi , zi . Следовательно,

W i ≈ P(ξi ηi ,νi ) xi + Q(ξi ηi ,νi ) yi + R(ξi ηi ,νi ) zi ) .

В таком случае вся работа сил поля будет приблизительно равна

n

W ≈ ∑(P(ξi ,ηi ,νi ) xi + Q(ξi ,ηi ,νi ) yi + R(ξi ,ηi ,νi ) zi ).

i=1

В качестве точного значения работы W естественно принять предел этой суммы при n→∞ и измельчении отрезков, на которые делится кривая L, т.е.

Отвлечемся теперь от физического содержания задачи и будем считать, что в некоторой области D пространства в окрестности пространственной кривойL, соединяющей точки A иB,определена некоторая функция

A0 = A ,A1,A2,A3,...,An = B,внутри каждого отрезка выбрать некоторую точку

Mi (ξi ,ηi ,νi )и сформировать интегральную сумму

i=1

то предел этой суммы при n→∞ и li →0 (если он существует и не зави-

сит от способа деления кривой AB и от выбора точек M(ξη,ν )) обознача-

i i i i

ется, как

111